 δις παραγωγίσιμη ώστε
δις παραγωγίσιμη ώστε  , και ο οριζόντιος άξονας εφάπτεται της
, και ο οριζόντιος άξονας εφάπτεται της  στην αρχή των αξόνων.
στην αρχή των αξόνων.1) Να βρεθεί ο τύπος της συνάρτησης και το σύνολο τιμών της
2) Nα λυθεί η ανίσωση

3) Να βρεθεί η οριζόντια ασύμπτωτη της
 στο
στο 
4) Να υπολογιστεί το

5) Να αποδειχθεί οτι η εξίσωση
 έχει δυο λύσεις ετερόσημες
έχει δυο λύσεις ετερόσημες6)
 ,
, 


 και
και 
![f''(x)+f'(x)=e^{-x}\Leftrightarrow [f'(x)+f(x)]'=(-e^{-x})'\Leftrightarrow \\\\ f'(x)+f(x)=-e^{-x}+c_{1} f''(x)+f'(x)=e^{-x}\Leftrightarrow [f'(x)+f(x)]'=(-e^{-x})'\Leftrightarrow \\\\ f'(x)+f(x)=-e^{-x}+c_{1}](/forum/ext/geomar/texintegr/latexrender/pictures/ac75d8a6ac883cbfe18c81ffdd1289bb.png)
 προκύπτει
προκύπτει 
 έχουμε :
έχουμε : 
 επομένως
επομένως 




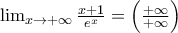 DLH=
DLH=

![f'(x)\leq 0 \Leftrightarrow x\leq 0 \Leftrightarrow f(x)\downarrow x\in(-\infty,0]\\\\ f'(x)\leq 0 \Leftrightarrow x\leq 0 \Leftrightarrow f(x)\downarrow x\in(-\infty,0]\\\\](/forum/ext/geomar/texintegr/latexrender/pictures/9913bb4fc889d78e8b108c3718d8699c.png)
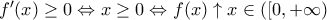

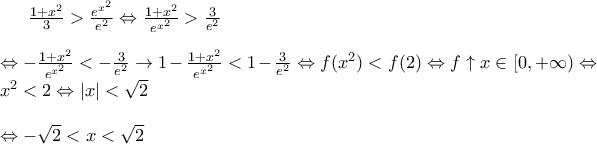

 είναι γνησίως αύξουσα για
είναι γνησίως αύξουσα για  με
με 
![[x+1,x+2017] [x+1,x+2017]](/forum/ext/geomar/texintegr/latexrender/pictures/a95867767d2f719862b8bfe22b2f52ec.png) και
και 


 μια παράγουσα της
μια παράγουσα της ![x\to +\infty \Leftrightarrow x+1\to +\infty\Leftrightarrow \lim_{x\to +\infty}f(x+1)=1\\\\x\to +\infty \Leftrightarrow x+2017\to +\infty\Leftrightarrow \lim_{x\to +\infty}f(x+2017)=1\\\\ 2016<\lim_{x\to +\infty}[F(x+2017)-F(x+1)]<2016\Leftrightarrow\\ \lim_{x\to +\infty}[F(x+2017)-F(x+1)]=2016 x\to +\infty \Leftrightarrow x+1\to +\infty\Leftrightarrow \lim_{x\to +\infty}f(x+1)=1\\\\x\to +\infty \Leftrightarrow x+2017\to +\infty\Leftrightarrow \lim_{x\to +\infty}f(x+2017)=1\\\\ 2016<\lim_{x\to +\infty}[F(x+2017)-F(x+1)]<2016\Leftrightarrow\\ \lim_{x\to +\infty}[F(x+2017)-F(x+1)]=2016](/forum/ext/geomar/texintegr/latexrender/pictures/49ab4c386c147363fd7d293df1b2abff.png)
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\displaystyle{\left( { - \infty ,0} \right]} \displaystyle{\left( { - \infty ,0} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ac38e9c7e5aa7ab14f64b51460ee5b0d.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![\displaystyle{\left( {0, + \infty } \right]} \displaystyle{\left( {0, + \infty } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/9bf92c9a8121a4d36b2840a00e9f3a1c.png) ενώ στα διαστήματα αυτά το σύνολο τιμών είναι
ενώ στα διαστήματα αυτά το σύνολο τιμών είναι  και
και 

 , θα είναι
, θα είναι  .Το
.Το  ανήκει και στα δύο διαστήματα του συνόλου τιμών και συνεπώς υπάρχουν λύσεις της
ανήκει και στα δύο διαστήματα του συνόλου τιμών και συνεπώς υπάρχουν λύσεις της  είναι κάπως πιο εύκολά τα
είναι κάπως πιο εύκολά τα 
