ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Δίνεται η

με

1)Δικαιολογήστε γιατί είναι συνεχής και δείξτε ότι έχει ολικό ελάχιστο σε ένα

2)Βρείτε το

για

και δείξτε ότι δεν παραγωγίζεται στο

3)Δείξτε ότι

4)Βρείτε το

και δείξτε ότι δεν έχει ασύμπτωτη στο

5)Δείξτε ότι η συνάρτηση είναι κοίλη στο

6)Δείξτε ότι υπάρχει

με

Η συνάρτηση αυτή είναι τυπικό παράδειγμα συνάρτησης που πάει στο

πιο 'γρήγορα' από οποιαδήποτε δύναμη του λογαρίθμου και πιο 'αργά' από οποιαδήποτε δύναμη του

Δηλαδή για


ενώ

(Δεν είναι και τόσο δύσκολα να αποδειχθούν)
...μιά αντιμετώπιση....
1) Είναι

για

και επειδή η

συνεχής στο

και η

συνεχής στο

και η

συνεχής στο

η

είναι συνεχής ως σύνθεση συνεχών και
επειδή

η

έχει ολικό ελάχιστο το

2) Είναι για

η

παραγωγίσιμη ως πράξεις παραγωγίσιμων με

οπότε παραγωγίζοντας έχουμε

και για

η

παραγωγίσιμη ως πράξεις παραγωγίσιμων με

οπότε παραγωγίζοντας έχουμε

δηλαδή

για
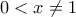
Τώρα στο

έχουμε ότι

άρα δεν είναι παραγωγίσιμη στο

.
3) Είναι

επειδή

4) Η

στο

έχει όριο

και

λόγω του (3) και έτσι επειδή

η

δεν έχει ασύμπτωτη στο

5) Είναι

επομένως


( αφού είναι

)
άρα η συνάρτηση είναι κοίλη στο

6) Θέλουμε η εξίσωση

να έχει λύση στο

Επειδή η

είναι γνήσια φθίνουσα στο

είναι

(για το

από (4) έχουμε

) και επειδή

υπάρχει μοναδικός

ώστε

...πολλές πράξεις...
Φιλικά και Μαθηματικά
Βασίλης



 για
για  και δείξτε ότι δεν παραγωγίζεται στο
και δείξτε ότι δεν παραγωγίζεται στο 

 και δείξτε ότι δεν έχει ασύμπτωτη στο
και δείξτε ότι δεν έχει ασύμπτωτη στο 









 και επειδή η
και επειδή η  συνεχής στο
συνεχής στο  και η
και η  συνεχής στο
συνεχής στο  και η
και η  συνεχής στο
συνεχής στο  η
η  είναι συνεχής ως σύνθεση συνεχών και
είναι συνεχής ως σύνθεση συνεχών και  η
η 
 η
η  παραγωγίσιμη ως πράξεις παραγωγίσιμων με
παραγωγίσιμη ως πράξεις παραγωγίσιμων με 

 η
η  παραγωγίσιμη ως πράξεις παραγωγίσιμων με
παραγωγίσιμη ως πράξεις παραγωγίσιμων με 
 δηλαδή
δηλαδή  για
για 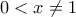
 έχουμε ότι
έχουμε ότι 


 στο
στο  έχει όριο
έχει όριο  και
και 
 η
η  επομένως
επομένως 
 ( αφού είναι
( αφού είναι  )
)
 Επειδή η
Επειδή η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο  είναι
είναι 
 από (4) έχουμε
από (4) έχουμε  ) και επειδή
) και επειδή 
 ώστε
ώστε 
