
παραγωγίσιμη με συνεχή παράγωγο στο

για την οποία ισχύουν
 παράγουσα της
παράγουσα της  στο
στο 

 για κάθε
για κάθε 
 όπου
όπου  η μεγαλύτερη ρίζα της εξίσωσης
η μεγαλύτερη ρίζα της εξίσωσης 
Δ1
Δείξτε ότι
 και στην συνέχεια ότι
και στην συνέχεια ότι  για κάθε
για κάθε 
Δ2
Μελετήστε την
 ως προς την κυρτότητα και τα σημεία καμπής και στην συνέχεια δείξτε
ως προς την κυρτότητα και τα σημεία καμπής και στην συνέχεια δείξτε ότι υπάρχει

Δ3
Δείξτε ότι η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και στην συνέχεια δείξτε ότι
και στην συνέχεια δείξτε ότι 
Πηγή Internet.Υπάρχει και το σχολείο που έχει δοθεί αλλά δεν κρίνω σκόπιμο να το αναφέρω.

 που έχει ρίζες τους
που έχει ρίζες τους  που είναι και οι μοναδικές
που είναι και οι μοναδικές  τότε για την συνάρτηση
τότε για την συνάρτηση  σύμφωνα με το Rolle στα
σύμφωνα με το Rolle στα ![[{{\rho }_{1}},\,{{\rho }_{2}}],\,\,[{{\rho }_{2}},\,{{\rho }_{3}}] [{{\rho }_{1}},\,{{\rho }_{2}}],\,\,[{{\rho }_{2}},\,{{\rho }_{3}}]](/forum/ext/geomar/texintegr/latexrender/pictures/e8ee2b147a2d7ff37ed884fdebf32cae.png) θα υπήρχαν
θα υπήρχαν  ώστε
ώστε 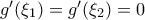 με
με  και από Rolle στο
και από Rolle στο ![[{{\xi }_{1}},\,{{\xi }_{2}}] [{{\xi }_{1}},\,{{\xi }_{2}}]](/forum/ext/geomar/texintegr/latexrender/pictures/867a2a7e2e2fce01c06f7eecefcc81a6.png) για την
για την  θα υπήρχε
θα υπήρχε 
 που είναι άτοπο, επομένως
που είναι άτοπο, επομένως  και τότε
και τότε 
 είναι
είναι  για
για  (…με δεδομένο ότι η
(…με δεδομένο ότι η  συνεχής )
συνεχής )  άρα η
άρα η  και θα διατηρεί σταθερό πρόσημο και αν
και θα διατηρεί σταθερό πρόσημο και αν  τότε
τότε  γνήσια φθίνουσα και τότε
γνήσια φθίνουσα και τότε 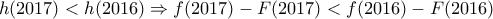
 και από
και από  ή
ή 

 άρα
άρα 
 και
και  Για τα
Για τα  ενώ για τα
ενώ για τα  συνεπώς η
συνεπώς η  και κοίλη στο
και κοίλη στο ![(0,1]. (0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/48fcc93577a0c42f47ffe011f5bde061.png) Το σημείο
Το σημείο  σημείο καμπής της
σημείο καμπής της 
![\displaystyle{g(x)=2f\left(\frac{3}{2x}\right)-f\left(\frac{1}{2x}\right)-f\left(\frac{5}{2x}\right),x\in\left[\frac{1}{2},e\right]}. \displaystyle{g(x)=2f\left(\frac{3}{2x}\right)-f\left(\frac{1}{2x}\right)-f\left(\frac{5}{2x}\right),x\in\left[\frac{1}{2},e\right]}.](/forum/ext/geomar/texintegr/latexrender/pictures/45966daa5a7b93df40c9da8bf60836b9.png) Παρατηρούμε ότι η
Παρατηρούμε ότι η  ικανοποιεί τις υποθέσεις του θ.Bolzano καθώς είναι συνεχής στο
ικανοποιεί τις υποθέσεις του θ.Bolzano καθώς είναι συνεχής στο ![\left[\frac{1}{2},e\right]} \left[\frac{1}{2},e\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/806def124acc143ca0ade35ef9618ce2.png) και
και  και
και  Tα πρόσημα προκύπτουν με εφαρμογή της ανισότητας Jensen για την
Tα πρόσημα προκύπτουν με εφαρμογή της ανισότητας Jensen για την ![[1,5] [1,5]](/forum/ext/geomar/texintegr/latexrender/pictures/9eba9937dac992e78a2abce3ef434e6a.png) και
και ![\displaystyle{\left[\frac{1}{2e},\frac{5}{2e}\right].} \displaystyle{\left[\frac{1}{2e},\frac{5}{2e}\right].}](/forum/ext/geomar/texintegr/latexrender/pictures/0b334dc82f24d0537168ed2b5681d0fc.png)
 άρα η
άρα η ![x\in[1,2] x\in[1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/c23eb188afbe73785d869321ba1cd4a7.png)

 και στα τρία μέλη της ανίσωσης και διαιρώντας με το
και στα τρία μέλη της ανίσωσης και διαιρώντας με το  έχουμε το ζητούμενο.
έχουμε το ζητούμενο.