Υπάρχει;
Συντονιστής: Μπάμπης Στεργίου
Υπάρχει;
Μια μεταμεσονύχτια γέννα
- Συνημμένα
-
- 4234.png (7.68 KiB) Προβλήθηκε 1564 φορές
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Υπάρχει;
Μία σκέψη μόνο Βασίλη :


S.E.Louridas


S.E.Louridas
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Υπάρχει;
Χεχε καλημέρα Σωτήρη.
Μία σκέψη κάτι παραπάνω από λύση θα έλεγα
Σπύρο χαίρομαι που σου άρεσε η άσκηση
Μία σκέψη κάτι παραπάνω από λύση θα έλεγα
Σπύρο χαίρομαι που σου άρεσε η άσκηση
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
-
k-ser
- Δημοσιεύσεις: 870
- Εγγραφή: Σάβ Δεκ 20, 2008 10:22 am
- Τοποθεσία: Μουζάκι Καρδίτσας
- Επικοινωνία:
Re: Υπάρχει;
Βασίλη, καλή άσκηση και πολύ καλή η απάντηση του Σωτήρη.
Χρειάζεται και η επιπλέον προϋπόθεση: η συνεχής.
συνεχής.
Αν δεν σου κάνει κόπο γράψε την σε latex.
Φιλικά.
Χρειάζεται και η επιπλέον προϋπόθεση: η
 συνεχής.
συνεχής.Αν δεν σου κάνει κόπο γράψε την σε latex.
Φιλικά.
Κώστας Σερίφης
Re: Υπάρχει;
Κώστα πράγματι ξέχασα την συνέχεια της παραγώγου. Χωρίς αυτήν το ολοκλήρωμα που γράφω δεν έχει λυκειακό νόημα
Δίνω την διορθωμένη εκφώνηση
Να εξετάσετε αν υπάρχει παραγωγίσιμη συνάρτηση
με συνεχή παράγωγο τέτοια ώστε
και![\displaystyle{\int\limits_0^1 {\left[ {{{\left( {f'\left( x \right)} \right)}^2} + f\left( x \right)} \right]dx} = \frac{1}{{24}}} \displaystyle{\int\limits_0^1 {\left[ {{{\left( {f'\left( x \right)} \right)}^2} + f\left( x \right)} \right]dx} = \frac{1}{{24}}}](/forum/ext/geomar/texintegr/latexrender/pictures/55875744a28c3b75774fba2fb4b0dd1c.png)
Να σημειώσω ότι έχει ενδιαφέρον η τελική απάντηση, τουλάχιστον για τους μαθητές μας
Δίνω την διορθωμένη εκφώνηση
Να εξετάσετε αν υπάρχει παραγωγίσιμη συνάρτηση

με συνεχή παράγωγο τέτοια ώστε

και
![\displaystyle{\int\limits_0^1 {\left[ {{{\left( {f'\left( x \right)} \right)}^2} + f\left( x \right)} \right]dx} = \frac{1}{{24}}} \displaystyle{\int\limits_0^1 {\left[ {{{\left( {f'\left( x \right)} \right)}^2} + f\left( x \right)} \right]dx} = \frac{1}{{24}}}](/forum/ext/geomar/texintegr/latexrender/pictures/55875744a28c3b75774fba2fb4b0dd1c.png)
Να σημειώσω ότι έχει ενδιαφέρον η τελική απάντηση, τουλάχιστον για τους μαθητές μας
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Υπάρχει;
Ας μου επιτραπεί ένα σχόλιο:
Η άσκηση αυτή κατά την άποψή μου έχει την ομορφιά να δημιουργεί ιδέες για κατασκευή και άλλων ασκήσεων (και ας αφήσουμε το σε ευχαριστώ για τα καλά σου λόγια κ.τ.λ. για να πάμε στην ουσία αφού ο ‘γάμος’ της πραγματικής αλληλοεκτίμησης είναι πλέον γεγονός) όπως το να σκεφτούμε :
Από το γεγονός (σύμφωνα με το σχολικό βιβλίο) ότι η ‘μέσα’ συνάρτηση στην περίπτωση ενός ορισμένου ολοκληρώματος είναι σ υ ν ε χ ή ς ,αυτόματα παίρνουμε ότι η
είναι συνεχής συνάρτηση καθότι θεωρούμε σε ισχύ (αληθής πρόταση) την ισότητα που στο αριστερό της μέλος υπάρχει το ορισμένο ολοκλήρωμα. Άρα το να δώσουμε την συνέχεια της παραγώγου
της f ( όσο με αφορά στην τεχνική επίλυσης που πρότεινα την έλαβα υπ’ όψη σαν δεδομένη οπότε σαν τεχνική παραμένει σε ισχύ) δημιουργείται το συγκεκριμένο πρόβλημα. Λαμβάνοντας ,όμως υπ’ όψη την συνέχεια της
για κάθε δεδομένο που οδηγεί από την συνέχεια εδώ στην συνέχεια της δημιουργούνται προϋποθέσεις κατασκευής προβλήματος.
δημιουργούνται προϋποθέσεις κατασκευής προβλήματος.
Για παράδειγμα: αν ,αντί για την συνέχεια της δινόταν ότι η f είναι γνήσια μονότονη αυτό οδηγεί ευθέως στην συνέχεια της
δινόταν ότι η f είναι γνήσια μονότονη αυτό οδηγεί ευθέως στην συνέχεια της  αφού έτσι έχουμε την διατήρηση πρόσημου κ.τ.λ..
αφού έτσι έχουμε την διατήρηση πρόσημου κ.τ.λ..
S.E.Louridas
Η άσκηση αυτή κατά την άποψή μου έχει την ομορφιά να δημιουργεί ιδέες για κατασκευή και άλλων ασκήσεων (και ας αφήσουμε το σε ευχαριστώ για τα καλά σου λόγια κ.τ.λ. για να πάμε στην ουσία αφού ο ‘γάμος’ της πραγματικής αλληλοεκτίμησης είναι πλέον γεγονός) όπως το να σκεφτούμε :
Από το γεγονός (σύμφωνα με το σχολικό βιβλίο) ότι η ‘μέσα’ συνάρτηση στην περίπτωση ενός ορισμένου ολοκληρώματος είναι σ υ ν ε χ ή ς ,αυτόματα παίρνουμε ότι η

είναι συνεχής συνάρτηση καθότι θεωρούμε σε ισχύ (αληθής πρόταση) την ισότητα που στο αριστερό της μέλος υπάρχει το ορισμένο ολοκλήρωμα. Άρα το να δώσουμε την συνέχεια της παραγώγου
της f ( όσο με αφορά στην τεχνική επίλυσης που πρότεινα την έλαβα υπ’ όψη σαν δεδομένη οπότε σαν τεχνική παραμένει σε ισχύ) δημιουργείται το συγκεκριμένο πρόβλημα. Λαμβάνοντας ,όμως υπ’ όψη την συνέχεια της

για κάθε δεδομένο που οδηγεί από την συνέχεια εδώ στην συνέχεια της
 δημιουργούνται προϋποθέσεις κατασκευής προβλήματος.
δημιουργούνται προϋποθέσεις κατασκευής προβλήματος. Για παράδειγμα: αν ,αντί για την συνέχεια της
 δινόταν ότι η f είναι γνήσια μονότονη αυτό οδηγεί ευθέως στην συνέχεια της
δινόταν ότι η f είναι γνήσια μονότονη αυτό οδηγεί ευθέως στην συνέχεια της  αφού έτσι έχουμε την διατήρηση πρόσημου κ.τ.λ..
αφού έτσι έχουμε την διατήρηση πρόσημου κ.τ.λ.. S.E.Louridas
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- Α.Κυριακόπουλος
- Δημοσιεύσεις: 988
- Εγγραφή: Κυρ Ιαν 04, 2009 9:49 am
- Τοποθεσία: ΧΟΛΑΡΓΟΣ
Re: Υπάρχει;
Αγαπητέ Σωτήρη.S.E.Louridas έγραψε:Ας μου επιτραπεί ένα σχόλιο:
Η άσκηση αυτή κατά την άποψή μου έχει την ομορφιά να δημιουργεί ιδέες για κατασκευή και άλλων ασκήσεων (και ας αφήσουμε το σε ευχαριστώ για τα καλά σου λόγια κ.τ.λ. για να πάμε στην ουσία αφού ο ‘γάμος’ της πραγματικής αλληλοεκτίμησης είναι πλέον γεγονός) όπως το να σκεφτούμε :
Από το γεγονός (σύμφωνα με το σχολικό βιβλίο) ότι η ‘μέσα’ συνάρτηση στην περίπτωση ενός ορισμένου ολοκληρώματος είναι σ υ ν ε χ ή ς ,αυτόματα παίρνουμε ότι η
είναι συνεχής συνάρτηση καθότι θεωρούμε σε ισχύ (αληθής πρόταση) την ισότητα που στο αριστερό της μέλος υπάρχει το ορισμένο ολοκλήρωμα. Άρα το να δώσουμε την συνέχεια της παραγώγου
της f ( όσο με αφορά στην τεχνική επίλυσης που πρότεινα την έλαβα υπ’ όψη σαν δεδομένη οπότε σαν τεχνική παραμένει σε ισχύ) δημιουργείται το συγκεκριμένο πρόβλημα. Λαμβάνοντας ,όμως υπ’ όψη την συνέχεια της
για κάθε δεδομένο που οδηγεί από την συνέχεια εδώ στην συνέχεια τηςδημιουργούνται προϋποθέσεις κατασκευής προβλήματος.
Για παράδειγμα: αν ,αντί για την συνέχεια τηςδινόταν ότι η f είναι γνήσια μονότονη αυτό οδηγεί ευθέως στην συνέχεια της
αφού έτσι έχουμε την διατήρηση πρόσημου κ.τ.λ..
S.E.Louridas
Δεν μπορώ να καταλάβω τι θέλεις να πεις με αυτά που γράφεις. Ο Κώστας ο Σερίφης έχει δίκιο.
Αντώνης Κυριακόπουλος
•Ο έξυπνος παραδέχεται •Ο πονηρός δικαιολογείται •Ο βλάκας επιμένει
•Ο έξυπνος παραδέχεται •Ο πονηρός δικαιολογείται •Ο βλάκας επιμένει
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Υπάρχει;
Μα προφανώς ο Κώστας Σερίφης έχει Δίκιο.
Απλά έκανα κάποιες σκέψεις ώστε να δίνεται έμμεσα η συνέχεια της παραγώγου αντί άμεσα. Εγώ ήδη στην τεχνική που ανέφερα και που οδηγεί στην επίληση της άσκησης έλαβα υπ' όψη την συνέχεια της f ' .
Θα ήθελα φίλε Αντώνη την γνώμη σου, αν και εφόσον έχεις λίγο χρόνο , γιά το πώς θα μπορούσε να δοθεί έμμεσα, διτηρώντας τα άλλα δεδομένα του προβλήματος ,η συνέχεια της f ', αυτό είναι όλο.
Σε ευχαριστώ,
S.E.Louridas
Απλά έκανα κάποιες σκέψεις ώστε να δίνεται έμμεσα η συνέχεια της παραγώγου αντί άμεσα. Εγώ ήδη στην τεχνική που ανέφερα και που οδηγεί στην επίληση της άσκησης έλαβα υπ' όψη την συνέχεια της f ' .
Θα ήθελα φίλε Αντώνη την γνώμη σου, αν και εφόσον έχεις λίγο χρόνο , γιά το πώς θα μπορούσε να δοθεί έμμεσα, διτηρώντας τα άλλα δεδομένα του προβλήματος ,η συνέχεια της f ', αυτό είναι όλο.
Σε ευχαριστώ,
S.E.Louridas
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Υπάρχει;
Καλό μεσημέρι.
Σωτήρη και κύριε Αντώνη, ο Κώστας θέλω να πιστεύω ότι επεσήμανε ,μία οφθαλμοφανή παράλειψη μου και όχι ένα λάθος το οποίο χρίζει ανάλυσης συζήτησης κτλ.
Εν ολίγοις αν κάπου, κάτι δεν έστεκε, δεν έστεκε εξαιτίας δικής μου υπαιτιότητας. Δεν είνα θέμα του ποιος έχει δίκιο ή όχι (δεν νομίζω ότι υπάρχει καμιά διαφωνία σε αυτό). Ας κρατήσουμε την ωραία λύση του Σωτήρη και ας επαναλάβω ότι καλό είναι να δώσουμε και το τελικό συμπέρασμα για την άσκηση, που ίσως είναι διδακτικό για τους μαθητές μας
Τυπικά να πω ότι η λύση μου είναι ατή του Σωτήρη.
Πράγματι η άσκηση αυτή δίνει μία "νέα" κατηγορία ασκήσεων με μεθοδολογική κάλυψη. Η άσκηση είναι δική μου, η ιδέα δεν είναι. Θεωρώ ότι η άσκηση είναι πρωτότυπη
Πιείτε καμιά παγωμένη λεμονάδα στην υγειά μου και δείτε μουντιάλ
Σωτήρη και κύριε Αντώνη, ο Κώστας θέλω να πιστεύω ότι επεσήμανε ,μία οφθαλμοφανή παράλειψη μου και όχι ένα λάθος το οποίο χρίζει ανάλυσης συζήτησης κτλ.
Εν ολίγοις αν κάπου, κάτι δεν έστεκε, δεν έστεκε εξαιτίας δικής μου υπαιτιότητας. Δεν είνα θέμα του ποιος έχει δίκιο ή όχι (δεν νομίζω ότι υπάρχει καμιά διαφωνία σε αυτό). Ας κρατήσουμε την ωραία λύση του Σωτήρη και ας επαναλάβω ότι καλό είναι να δώσουμε και το τελικό συμπέρασμα για την άσκηση, που ίσως είναι διδακτικό για τους μαθητές μας
Τυπικά να πω ότι η λύση μου είναι ατή του Σωτήρη.
Πράγματι η άσκηση αυτή δίνει μία "νέα" κατηγορία ασκήσεων με μεθοδολογική κάλυψη. Η άσκηση είναι δική μου, η ιδέα δεν είναι. Θεωρώ ότι η άσκηση είναι πρωτότυπη
Πιείτε καμιά παγωμένη λεμονάδα στην υγειά μου και δείτε μουντιάλ
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Α.Κυριακόπουλος
- Δημοσιεύσεις: 988
- Εγγραφή: Κυρ Ιαν 04, 2009 9:49 am
- Τοποθεσία: ΧΟΛΑΡΓΟΣ
Re: Υπάρχει;
Αγαπητέ Βασίλη.
Εγώ δεν είπα τη λέξη «λάθος». Απλά είπα ότι ο Κώστας έχει δίκαιο που επεσήμανε την παράλειψη. Ο Σωτήρης, όπως εξήγησε, λέει ότι αν από αυτή την άσκηση μπορούμε να βγάλουμε και κάτι άλλο. Ο Σωτήρης ,όπως πάντα, σκέπτεται δημιουργικά. Είναι ένα από τα πολλά προσόντα του.
Με εκτίμηση και αγάπη.
Εγώ δεν είπα τη λέξη «λάθος». Απλά είπα ότι ο Κώστας έχει δίκαιο που επεσήμανε την παράλειψη. Ο Σωτήρης, όπως εξήγησε, λέει ότι αν από αυτή την άσκηση μπορούμε να βγάλουμε και κάτι άλλο. Ο Σωτήρης ,όπως πάντα, σκέπτεται δημιουργικά. Είναι ένα από τα πολλά προσόντα του.
Με εκτίμηση και αγάπη.
Αντώνης Κυριακόπουλος
•Ο έξυπνος παραδέχεται •Ο πονηρός δικαιολογείται •Ο βλάκας επιμένει
•Ο έξυπνος παραδέχεται •Ο πονηρός δικαιολογείται •Ο βλάκας επιμένει
Re: Υπάρχει;
Συγγνώμη που ξεθάβω αυτό το θέμα, απλά αναρωτιέμαι αν το τελείωμα θα μπορούσε να είναι κάπως έτσι:

οπότε υπάρχει ώστε
ώστε

επομένως , άτοπο αφού
, άτοπο αφού  Μήπως υπάρχει κάτι πιο άμεσο;
Μήπως υπάρχει κάτι πιο άμεσο;

οπότε υπάρχει
 ώστε
ώστε 
επομένως
 , άτοπο αφού
, άτοπο αφού  Μήπως υπάρχει κάτι πιο άμεσο;
Μήπως υπάρχει κάτι πιο άμεσο;Κώστας
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: Υπάρχει;
styt_geia έγραψε:Συγγνώμη που ξεθάβω αυτό το θέμα, απλά αναρωτιέμαι αν το τελείωμα θα μπορούσε να είναι κάπως έτσι:
οπότε υπάρχειώστε
επομένως, άτοπο αφού
Μήπως υπάρχει κάτι πιο άμεσο;
Ο τύπος
 ισχύει για κάθε
ισχύει για κάθε ![x\in [0,1]... x\in [0,1]...](/forum/ext/geomar/texintegr/latexrender/pictures/dec71efab7bb4ae2dcfc03696096bcdd.png)
Θανάσης Κοντογεώργης
Re: Υπάρχει;
Σωστά, με παραπλάνησε το πεδίο ορισμού. Άλλη μία προσπάθεια. Είναι

οπότε

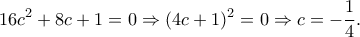
Επομένως , άτοπο.
, άτοπο.

οπότε

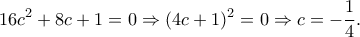
Επομένως
 , άτοπο.
, άτοπο.Κώστας
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
