Demetres έγραψε:Demetres έγραψε:Ζητήθηκαν ασκήσεις συνδυαστικής και γεωμετρίας. Ας δώσω 2 σε 1.
ΑΣΚΗΣΗ 8: Δίνονται

ευθείες στο επίπεδο οι οποίες το διαμερίζουν σε κάποια χωρία. Έστω

ο μέγιστος αριθμός από αυτά τα χωρία ώστε ανά δύο να μην είναι γειτονικά. (Επιτρέπεται να έχουν κοινή κορυφή αλλά όχι κοινό ευθύγραμμο τμήμα.) Να δειχθεί ότι

Βοήθεια: Έστω
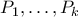
αυτά τα χωρία. Μετρήστε με δυο διαφορετικούς τρόπους τα ζεύγη

όπου η ευθεία

είναι μια από τις πλευρές του

. Είναι πιο απλό να δείξετε ότι
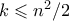
.
Λογάριαζα να ανεβάσω την λύση μου χθες, παραμονή του διαγωνισμού αλλά ξεχάστηκα.
Μετράω τα ζεύγη

όπως πιο πάνω. Αν για κάποιο

υπάρχει μόνο ένα

τότε όλες οι ευθείες είναι παράλληλες οπότε

αφού

.
Μπορώ λοιπόν να υποθέσω πως για κάθε

υπάρχουν τουλάχιστον δύο

και άρα ο αριθμός των ζευγών είναι τουλάχιστον

. Από την άλλη κάθε

διαμερίζεται σε

ευθύγραμμα τμήματα (ή ημιευθείες) από τις υπόλοιπες ευθείες. Κάθε τέτοιο τμήμα ανήκει το πολύ σε ένα

αφού τα

είναι ανά δύο μη γειτονικά. Άρα για κάθε

υπάρχουν το πολύ


και άρα ο συνολικός αριθμός ζευγών είναι το πολύ

.
Αυτό δίνει το πιο απλό
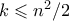
. Για το
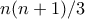
ας ονομάζουμε με

τον αριθμό των

για τα οποία υπάρχουν ακριβώς δύο

. Τότε και οι δύο πλευρές του

είναι ημιευθείες και επειδή ακριβώς
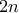
ημιευθείες υπάρχουν το πολύ

τέτοια

. Κάθε άλλο από τα

χρησιμοποιεί τουλάχιστον τρία

και άρα ο συνολικός αριθμός ζευγών είναι τουλάχιστον

. Οπότε
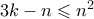
που δίνει το ζητούμενο.
είναι θετικοί πραγματικοί αριθμοί με
να αποδειχθεί ότι
.
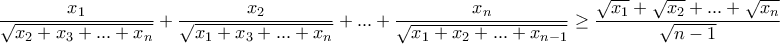
 .
. .
.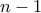 φορές και προσθέτοντας κατά μέλη έχουμε:
φορές και προσθέτοντας κατά μέλη έχουμε:






 αποδείξτε ότι
αποδείξτε ότι 

 έχουμε
έχουμε
 που ικανοποιεί την εξίσωση
που ικανοποιεί την εξίσωση 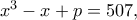 όπου
όπου  πρώτος αριθμός.
πρώτος αριθμός. των ακεραίων αριθμών που ικανοποιούν την εξίσωση:
των ακεραίων αριθμών που ικανοποιούν την εξίσωση: 
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  ως γινόμενο τριών διαδοχικών ακεραίων. Άρα
ως γινόμενο τριών διαδοχικών ακεραίων. Άρα 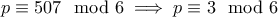 και επειδή
και επειδή  πρώτος, είναι
πρώτος, είναι  Τότε βρίσκουμε εύκολα
Τότε βρίσκουμε εύκολα 
 ώστε ο αριθμός
ώστε ο αριθμός 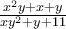 να είναι επίσης φυσικός.
να είναι επίσης φυσικός. ,
,  το οθόκεντρο και
το οθόκεντρο και  το περίκεντρό του. Αν η διχοτόμος της γωνίας
το περίκεντρό του. Αν η διχοτόμος της γωνίας  τέμνει κάθετα το τμήμα
τέμνει κάθετα το τμήμα  , να βρεθεί το μέτρο της
, να βρεθεί το μέτρο της  είναι διάφορη των
είναι διάφορη των  και να καταλήξω σε άτοπο, αλλά συζητώντας στο τηλέφωνο με τον Στάθη
και να καταλήξω σε άτοπο, αλλά συζητώντας στο τηλέφωνο με τον Στάθη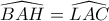 και αφού
και αφού 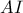 διχοτόμος άρα
διχοτόμος άρα  και συνεπώς , δεδομένου ότι
και συνεπώς , δεδομένου ότι , το τρίγωνο
, το τρίγωνο  είναι ισοσκελές και άρα το τετράπλευρο
είναι ισοσκελές και άρα το τετράπλευρο  είναι ρόμβος. Άρα
είναι ρόμβος. Άρα  , όπου
, όπου είναι η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου
είναι η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου  . Γνωρίζουμε όμως ότι
. Γνωρίζουμε όμως ότι  και άρα
και άρα είναι πλευρά ισοπλεύρου τριγώνου εγγεγραμμένου στον κύκλο
είναι πλευρά ισοπλεύρου τριγώνου εγγεγραμμένου στον κύκλο  . Συνεπώς θα είναι
. Συνεπώς θα είναι 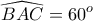 .
.  και
και  , τότε
, τότε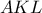 είναι ισόπλευρο.
είναι ισόπλευρο. ευθείες στο επίπεδο οι οποίες το διαμερίζουν σε κάποια χωρία. Έστω
ευθείες στο επίπεδο οι οποίες το διαμερίζουν σε κάποια χωρία. Έστω  ο μέγιστος αριθμός από αυτά τα χωρία ώστε ανά δύο να μην είναι γειτονικά. (Επιτρέπεται να έχουν κοινή κορυφή αλλά όχι κοινό ευθύγραμμο τμήμα.) Να δειχθεί ότι
ο μέγιστος αριθμός από αυτά τα χωρία ώστε ανά δύο να μην είναι γειτονικά. (Επιτρέπεται να έχουν κοινή κορυφή αλλά όχι κοινό ευθύγραμμο τμήμα.) Να δειχθεί ότι 
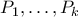 αυτά τα χωρία. Μετρήστε με δυο διαφορετικούς τρόπους τα ζεύγη
αυτά τα χωρία. Μετρήστε με δυο διαφορετικούς τρόπους τα ζεύγη  όπου η ευθεία
όπου η ευθεία  είναι μια από τις πλευρές του
είναι μια από τις πλευρές του  . Είναι πιο απλό να δείξετε ότι
. Είναι πιο απλό να δείξετε ότι 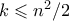 .
. .Έστω
.Έστω  τυχαίο σημείο του τόξου
τυχαίο σημείο του τόξου  και έστω
και έστω  τα ορθόκεντρα των
τα ορθόκεντρα των  αντίστοιχα.Τέλος ονομάζουμε
αντίστοιχα.Τέλος ονομάζουμε  τις προβολές του
τις προβολές του 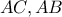 αντίστοιχα.Να αποδείξετε ότι η
αντίστοιχα.Να αποδείξετε ότι η  διχοτομεί το τμήμα
διχοτομεί το τμήμα 
 το σημείο τομής του εκ του
το σημείο τομής του εκ του  ύψους του τριγώνου
ύψους του τριγώνου  με τον περίκυκλο
με τον περίκυκλο  του τριγώνου
του τριγώνου  . Τότε με
. Τότε με 

 το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου  .
.  είναι η ευθεία
είναι η ευθεία  του
του  , με
, με  που διέρχεται από το
που διέρχεται από το  .Αν
.Αν  τα ορθόκεντρα των τριγώνων
τα ορθόκεντρα των τριγώνων 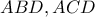 να δειχθεί ότι
να δειχθεί ότι  .
.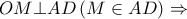
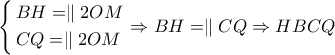 παραλληλόγραμμο οπότε
παραλληλόγραμμο οπότε  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. ως προς το μέσο της
ως προς το μέσο της  .
. αφού
αφού  . Από την άλλη κάθε
. Από την άλλη κάθε  ευθύγραμμα τμήματα (ή ημιευθείες) από τις υπόλοιπες ευθείες. Κάθε τέτοιο τμήμα ανήκει το πολύ σε ένα
ευθύγραμμα τμήματα (ή ημιευθείες) από τις υπόλοιπες ευθείες. Κάθε τέτοιο τμήμα ανήκει το πολύ σε ένα  .
.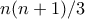 ας ονομάζουμε με
ας ονομάζουμε με  τον αριθμό των
τον αριθμό των 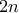 ημιευθείες υπάρχουν το πολύ
ημιευθείες υπάρχουν το πολύ  . Οπότε
. Οπότε 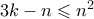 που δίνει το ζητούμενο.
που δίνει το ζητούμενο. .
. παίρνουμε
παίρνουμε 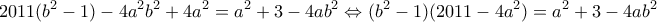 .
. και έχουμε
και έχουμε  .
.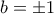 παίρνουμε τις λύσεις
παίρνουμε τις λύσεις  .
. .Ο δεύτερος παράγοντας του πρώτου μέλους είναι περιττός οπότε δεν μηδενίζεται.
.Ο δεύτερος παράγοντας του πρώτου μέλους είναι περιττός οπότε δεν μηδενίζεται.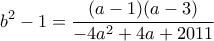 .
. θα ισχύει
θα ισχύει  .
.
 .Η μόνη τιμή που παίρνει ο
.Η μόνη τιμή που παίρνει ο  είναι
είναι  που μπορούμε εύκολα να απορρίψουμε.
που μπορούμε εύκολα να απορρίψουμε. .
. .
. περιττός είναι
περιττός είναι  .
.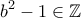 θα είναι
θα είναι  .
. .
. ή
ή  .
. που δεν δίνουν λύση.
που δεν δίνουν λύση.
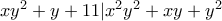 (*)
(*)  (**)
(**) και εδώ διακρίνουμε 2 περιπτώσεις
και εδώ διακρίνουμε 2 περιπτώσεις 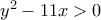 τότε
τότε  και εφόσον
και εφόσον 


 αφήνεται και αυτό για τον αναγνώστη.
αφήνεται και αυτό για τον αναγνώστη.