socrates έγραψε: ↑Πέμ Μαρ 05, 2020 1:24 am
ΘΕΜΑ 3
Έστω
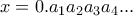
και
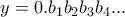
οι δεκαδικές αναπαραστάσεις των θετικών πραγματικών αριθμών

και
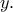
Υποθέτουμε ότι
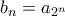
για κάθε

Να δείξετε ότι αν ο

είναι ρητός, τότε και ο

είναι ρητός.
Δύσκολο. Ας κάνω μια προσπάθεια.
Έστω
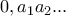
η δεκαδική αναπαράσταση των ψηφίων ενός δεκαδικού αριθμού και
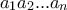
η δεκαδική αναπαράσταση ακεραίου αριθμού. Θα ασχοληθώ μόνο με κλασματικά μέρη καθώς τα ακέραια μέρη δεν επηρεάζουν τη λύση διότι αν έχω ρητό με αριθμητή μεγαλύτερο του παρονομαστή απλά εκτελώ ευκλείδια διαίρεση και συνεχίζω με το κλασματικό. Θα θεωρήσω δεκαδικούς με άπειρα ψηφία.
Ξεκινάω:
Λήμμα 1: Αν η δεκαδική αναπαράσταση δεκαδικού είναι περιοδική από ένα σημείο και πέρα, τότε αυτός είναι ρητός
Απόδειξη:
1η ειδική περίπτωση:
Θεωρώ τον:
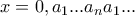
Τότε:
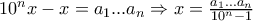
. Άρα

ρητός.
Γενικεύοντας για να αποδείξω το λήμμα:
Θεωρώ τον
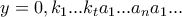
Τότε:
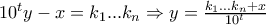
άρα

ρητός και το λήμμα απεδείχθη.
Λήμμα 2: Η δεκαδική αναπαράσταση κάθε ρητού είναι περιοδική από ένα σημείο και πέρα (άσκηση στις σημειώσεις του κ.Κοντοκώστα Δημήτρη-αν δεν κάμω λάθος-):
Απόδειξη (edit: αχρείαστη όπως επισημαίνει ο κ.Σταύρος παρακάτω):
Θεωρώ:
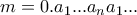
,
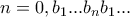
ώστε:

. Σκεπτόμενος όπως στο Λήμμα 1
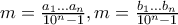
.
Τότε η διαφορά

ορίζει ρητό της μορφής
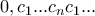
.
Έστω τώρα ρητός

με
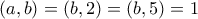
και
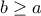
. Σκοπός μου είναι να αποδείξω ότι γίνεται
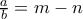
. Πράγματι:
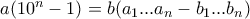
καθώς μπορώ να πάρω

ώστε
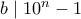
(πχ
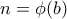
) και η διαφορά
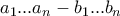
παίρνει κάθε αριθμό από 1 εώς και
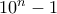
.
Ολοκληρώνω το λήμμα θεωρώντας ρητό
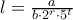
με τους ίδους περιορισμούς στον ΜΚΔ με πριν. WLOG
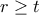
. Τότε
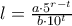
. Το
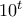
ως δεν επηρεάζει τη δεκαδική αναπαράσταση. Άρα αν εξαιρέσω τα μηδενικά, ο

έχει ίδια δεκαδική αναπαράσταση με τον
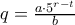
. Άγοντας τον

σε μικρότερο της μονάδας καταλήγω στην αρχή του λήμματος 2 και το ζητούμενο έπεται.
Προχωράω στη λύση.
Το ότι το

είναι ρητός μου δίνει από το Λήμμα 2 ότι από κάποιο σημείο και πέρα τα ψηφία του ορίζουν περιοδική ακολουθία. Αν αποδείξω το ίδιο για τον

, από Λήμμα 1 έχω το ζητούμενο.
Έστω

ο όρος που με εισάγει στην περιοδική ακολουθία (πχ στον
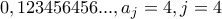
).
Ας είναι
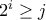
με τον ελάχιστο

.
Εφόσον η ακολουθία των ψηφίων του

είναι περιοδική και άπειρη, μπορώ να αναθεωρήσω ως αρχή της τον
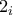
.
Ας είναι

η περίοδος της ακολουθίας, δηλαδή
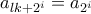
.
Ορίζω
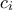
εκείνη την ακολουθία για την οποία
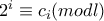
.
Αν αποδείξω ότι
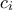
περιοδική τελείωσα.
Αν

περιττός, τότε άμεσο από την τάξη του
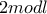
.
Αν

άρτιος:
Θα δείξω την περίπτωση που
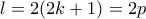
.
Τα άλλα ομοίως.
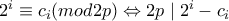
Άρα
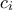
άρτιος και έστω
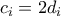
.
Τότε
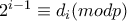
το οποίο με άγει στην πρώτη περίπτωση. Άρα

περιοδική οπότε
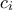
περιοδική και το ζητούμενο έπεται.
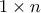 αποτελείται από
αποτελείται από  μοναδιαία τετράγωνα
μοναδιαία τετράγωνα 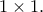 Βάφουμε καθένα από τα μοναδιαία τετράγωνα είτε κόκκινο, είτε μπλε, είτε πράσινο. Έστω
Βάφουμε καθένα από τα μοναδιαία τετράγωνα είτε κόκκινο, είτε μπλε, είτε πράσινο. Έστω  το πλήθος των χρωματισμών της λωρίδας στους οποίους υπάρχει περιττός αριθμός κόκκινων τετραγώνων. Να προσδιορίσετε τη μεγαλύτερη δύναμη του 2 που διαιρεί τον αριθμό
το πλήθος των χρωματισμών της λωρίδας στους οποίους υπάρχει περιττός αριθμός κόκκινων τετραγώνων. Να προσδιορίσετε τη μεγαλύτερη δύναμη του 2 που διαιρεί τον αριθμό 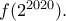
 τέτοιες ώστε
τέτοιες ώστε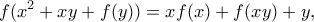 για κάθε
για κάθε 
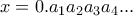 και
και 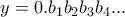 οι δεκαδικές αναπαραστάσεις των θετικών πραγματικών αριθμών
οι δεκαδικές αναπαραστάσεις των θετικών πραγματικών αριθμών  και
και 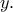
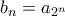 για κάθε
για κάθε  Να δείξετε ότι αν ο
Να δείξετε ότι αν ο  είναι ρητός, τότε και ο
είναι ρητός, τότε και ο  είναι ρητός.
είναι ρητός.  εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  και
και  το έγκεντρό του. Έστω
το έγκεντρό του. Έστω  και
και  τα σημεία τομής των
τα σημεία τομής των  και
και  με τον
με τον 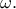 H
H  τέμνει τις πλευρές
τέμνει τις πλευρές  και
και  στα
στα  και
και  αντίστοιχα. Έστω
αντίστοιχα. Έστω 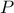 σημείο τέτοιο ώστε
σημείο τέτοιο ώστε 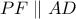 και
και 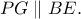
 στα
στα  και
και  τέμνονται στο
τέμνονται στο  Να αποδείξετε ότι οι ευθείες
Να αποδείξετε ότι οι ευθείες 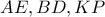 είναι είτε παράλληλες είτε συντρέχουσες.
είναι είτε παράλληλες είτε συντρέχουσες.
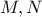 οι τομές των
οι τομές των 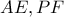 και
και 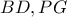 αντίστοιχα. Κατασκευάζουμε τα παραλληλόγραμμα
αντίστοιχα. Κατασκευάζουμε τα παραλληλόγραμμα 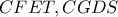 .
.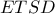 είναι εγγράψιμο ως ισοσκελές τραπέζιο αφού
είναι εγγράψιμο ως ισοσκελές τραπέζιο αφού 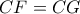 (απλό).
(απλό).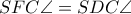 (
(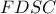 ισοσκελές τραπέζιο)
ισοσκελές τραπέζιο)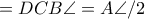 ,δηλαδή
,δηλαδή 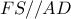 ,δηλαδή
,δηλαδή 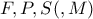 συνευθειακά.Ομοίως,
συνευθειακά.Ομοίως,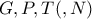 συνευθειακά.
συνευθειακά.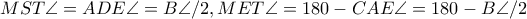 .Συνεπώς
.Συνεπώς 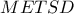 εγγράψιμο και όμοια
εγγράψιμο και όμοια 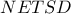 εγγράψιμο,δηλαδή
εγγράψιμο,δηλαδή 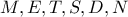 ομοκυκλικά.
ομοκυκλικά. είναι
είναι 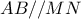 .
.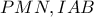 ,η τομή των
,η τομή των 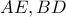 έστω
έστω  ανήκει στην
ανήκει στην 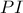 .Τέλος από
.Τέλος από  στο
στο 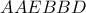 παίρνουμε πως
παίρνουμε πως 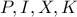 συνευθειακά κλπ.
συνευθειακά κλπ.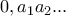 η δεκαδική αναπαράσταση των ψηφίων ενός δεκαδικού αριθμού και
η δεκαδική αναπαράσταση των ψηφίων ενός δεκαδικού αριθμού και 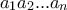 η δεκαδική αναπαράσταση ακεραίου αριθμού. Θα ασχοληθώ μόνο με κλασματικά μέρη καθώς τα ακέραια μέρη δεν επηρεάζουν τη λύση διότι αν έχω ρητό με αριθμητή μεγαλύτερο του παρονομαστή απλά εκτελώ ευκλείδια διαίρεση και συνεχίζω με το κλασματικό. Θα θεωρήσω δεκαδικούς με άπειρα ψηφία.
η δεκαδική αναπαράσταση ακεραίου αριθμού. Θα ασχοληθώ μόνο με κλασματικά μέρη καθώς τα ακέραια μέρη δεν επηρεάζουν τη λύση διότι αν έχω ρητό με αριθμητή μεγαλύτερο του παρονομαστή απλά εκτελώ ευκλείδια διαίρεση και συνεχίζω με το κλασματικό. Θα θεωρήσω δεκαδικούς με άπειρα ψηφία.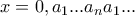
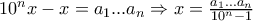 . Άρα
. Άρα 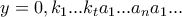
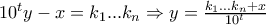 άρα
άρα 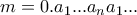 ,
, 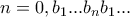
 . Σκεπτόμενος όπως στο Λήμμα 1
. Σκεπτόμενος όπως στο Λήμμα 1 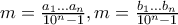 .
. ορίζει ρητό της μορφής
ορίζει ρητό της μορφής 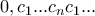 .
.  με
με 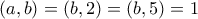 και
και 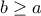 . Σκοπός μου είναι να αποδείξω ότι γίνεται
. Σκοπός μου είναι να αποδείξω ότι γίνεται 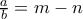 . Πράγματι:
. Πράγματι: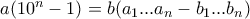 καθώς μπορώ να πάρω
καθώς μπορώ να πάρω 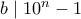 (πχ
(πχ 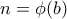 ) και η διαφορά
) και η διαφορά 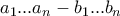 παίρνει κάθε αριθμό από 1 εώς και
παίρνει κάθε αριθμό από 1 εώς και 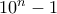 .
. 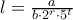 με τους ίδους περιορισμούς στον ΜΚΔ με πριν. WLOG
με τους ίδους περιορισμούς στον ΜΚΔ με πριν. WLOG 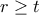 . Τότε
. Τότε 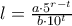 . Το
. Το 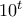 ως δεν επηρεάζει τη δεκαδική αναπαράσταση. Άρα αν εξαιρέσω τα μηδενικά, ο
ως δεν επηρεάζει τη δεκαδική αναπαράσταση. Άρα αν εξαιρέσω τα μηδενικά, ο  έχει ίδια δεκαδική αναπαράσταση με τον
έχει ίδια δεκαδική αναπαράσταση με τον 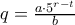 . Άγοντας τον
. Άγοντας τον  σε μικρότερο της μονάδας καταλήγω στην αρχή του λήμματος 2 και το ζητούμενο έπεται.
σε μικρότερο της μονάδας καταλήγω στην αρχή του λήμματος 2 και το ζητούμενο έπεται. ο όρος που με εισάγει στην περιοδική ακολουθία (πχ στον
ο όρος που με εισάγει στην περιοδική ακολουθία (πχ στον 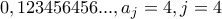 ).
).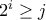 με τον ελάχιστο
με τον ελάχιστο  .
.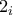 .
.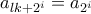 .
. 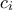 εκείνη την ακολουθία για την οποία
εκείνη την ακολουθία για την οποία 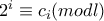 .
.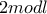 .
.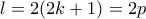 .
.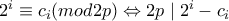
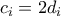 .
.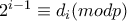 το οποίο με άγει στην πρώτη περίπτωση. Άρα
το οποίο με άγει στην πρώτη περίπτωση. Άρα  περιοδική οπότε
περιοδική οπότε 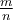 ο θετικός ρητός.
ο θετικός ρητός.
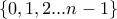
 .
. η δοσμένη συναρτησιακή σχέση.
η δοσμένη συναρτησιακή σχέση.
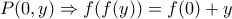 , οπότε η
, οπότε η  είναι 1-1. Για
είναι 1-1. Για  η προηγούμενη δίνει
η προηγούμενη δίνει 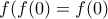 , άρα
, άρα  . Οπότε είναι
. Οπότε είναι 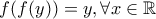 .
.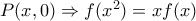 . Συνεπώς,
. Συνεπώς, 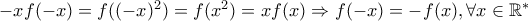 , και αφού
, και αφού 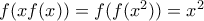 , και άρα
, και άρα 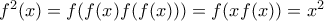 , συνεπώς
, συνεπώς  ή
ή  , για κάθε
, για κάθε  .
. . Διακρίνω 2 περιπτώσεις:
. Διακρίνω 2 περιπτώσεις: .
. 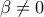 , ώστε
, ώστε 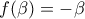 , τότε
, τότε 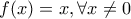 , οπότε
, οπότε 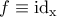 .
. . WLOG
. WLOG 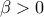 (αν
(αν 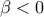 τότε απλά επιλέγω αντί του
τότε απλά επιλέγω αντί του 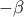 , αφού
, αφού 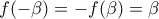 ).
). 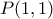 δίνει άμεσα
δίνει άμεσα 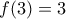 .
.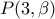 δίνει τώρα
δίνει τώρα 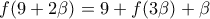 .
. Αν
Αν 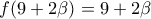 , τότε
, τότε  , οπότε
, οπότε 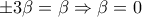 , άτοπο.
, άτοπο.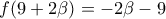 , τότε
, τότε 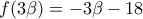 , οπότε
, οπότε 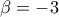 , άτοπο.
, άτοπο.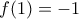 .
.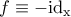 .
.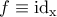 και
και 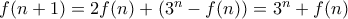 αφού έχουμε
αφού έχουμε 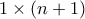 λωρίδας που μας ενδιαφέρουν με το τελευταίο τετράγωνο πράσινο,
λωρίδας που μας ενδιαφέρουν με το τελευταίο τετράγωνο πράσινο, 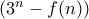 με το τελευταίο τετράγωνο κόκκινο.
με το τελευταίο τετράγωνο κόκκινο. , παίρνουμε
, παίρνουμε 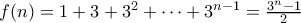 .
.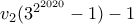 . Από Lifting the Exponent έχουμε
. Από Lifting the Exponent έχουμε 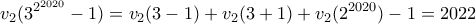
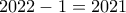 .
. είναι εν τέλει περιοδική. Έστω θετικοί ακέραιοι
είναι εν τέλει περιοδική. Έστω θετικοί ακέραιοι 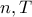 με
με 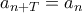 για κάθε
για κάθε  . Γράφουμε
. Γράφουμε 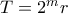 με
με  περιττό. Ισχυρίζομαι ότι
περιττό. Ισχυρίζομαι ότι 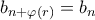 για κάθε
για κάθε 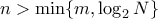 . Πράγματι τότε
. Πράγματι τότε 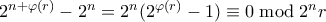 από Euler. Άρα και
από Euler. Άρα και 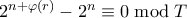 . Επειδή επιπλέον
. Επειδή επιπλέον 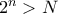 , τότε
, τότε 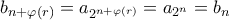 . Άρα και η ακολουθία
. Άρα και η ακολουθία  είναι εν τέλει περιοδική οπότε και ο
είναι εν τέλει περιοδική οπότε και ο  έχουμε
έχουμε 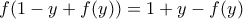 οπότε
οπότε