α) Αν
 να αποδείξετε ότι
να αποδείξετε ότι 
β) Αν
 και
και  να αποδείξετε ότι
να αποδείξετε ότι  .
.Θέμα 2ο
α) Να προσδιορίσετε πολυώνυμο
 2ου βαθμού που έχει τις ιδιότητες:
2ου βαθμού που έχει τις ιδιότητες:i) Διαιρούμενο με
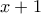 δίνει υπόλοιπο 32.
δίνει υπόλοιπο 32.ii) Το άθροισμα των συντελεστών του είναι 12 και ο σταθερός όρος 10.
β) Να προσδιορίσετε πολυώνυμο
 4ου βαθμού ώστε:
4ου βαθμού ώστε:
γ) Να υπολογίσετε το
 όπου
όπου  .
.Θέμα 3ο
α) Να αποδείξετε ότι ο αριθμός
 (
( ) είναι άθροισμα δύο τετραγώνων.
) είναι άθροισμα δύο τετραγώνων.β) Στο σύστημα αρίθμησης με βάση τον αριθμό
 (
( ) ισχύει:
) ισχύει:i) Ο αριθμός
 είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.ii) Ο αριθμός
 είναι τέλειος κύβος.
είναι τέλειος κύβος.iii) Ο αριθμός
 είναι τέλεια τέταρτη δύναμη.
είναι τέλεια τέταρτη δύναμη.Θέμα 4ο
α) Πόσοι αριθμοί μεγαλύτεροι του 2000 κατασκευάζονται από τα ψηφία 0,1,3,5,7 ;
β) Πόσοι αριθμοί με διαφορετικά ψηφία μεγαλύτεροι από το 2000 κατασκευάζονται από τα ψηφία 0,1,3,5,7;
Αλέξανδρος

 .Αν
.Αν  .Αρκεί λοιπόν να αποδείξουμε (αντικαθιστώντας τις μεταβλητές με αριθμούς) οτι
.Αρκεί λοιπόν να αποδείξουμε (αντικαθιστώντας τις μεταβλητές με αριθμούς) οτι  .
. και
και  .Καταλήγουμε στη σχέση:
.Καταλήγουμε στη σχέση:  (αποδείχτηκε).
(αποδείχτηκε). άρια,άπειρα
άρια,άπειρα  ,άπειρα
,άπειρα  ,άπειρα
,άπειρα  άρια και
άρια και  άρια).
άρια).
 από την
από την 

 .Κάνοντας Ευκλείδια Διαίρεση του
.Κάνοντας Ευκλείδια Διαίρεση του  είναι ο τύπος,με
είναι ο τύπος,με  ) βρίσκουμε:
) βρίσκουμε:  .
.
 είναι περιττός τότε έχουμε
είναι περιττός τότε έχουμε  . Αν
. Αν 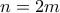 άρτιος τότε έχουμε
άρτιος τότε έχουμε  . Αν απαγορεύεται να χρησιμοποιήσουμε το
. Αν απαγορεύεται να χρησιμοποιήσουμε το  .
. . Ομοίως
. Ομοίως  και
και  .
. πενταψήφιους αριθμούς με την ζητούμενη ιδιότητα. Αν είναι τετραψήφιος τότε για το πρώτο ψηφίο έχουμε 3 επιλογές (τα 0,1 απαγορεύονται) για το δεύτερο 4 κ.τ.λ. Συνολικά έχουμε
πενταψήφιους αριθμούς με την ζητούμενη ιδιότητα. Αν είναι τετραψήφιος τότε για το πρώτο ψηφίο έχουμε 3 επιλογές (τα 0,1 απαγορεύονται) για το δεύτερο 4 κ.τ.λ. Συνολικά έχουμε  επιλογές. Άρα τελικά υπάρχουν
επιλογές. Άρα τελικά υπάρχουν  τέτοιοι αριθμοί.
τέτοιοι αριθμοί. . Τότε
. Τότε  οπότε με εξίσωση των συντελεστών βγάζουμε ότι
οπότε με εξίσωση των συντελεστών βγάζουμε ότι  οπότε το ζητούμενο πολυώνυμο είναι το
οπότε το ζητούμενο πολυώνυμο είναι το  με
με  αυθαίρετα.
αυθαίρετα. .
.