Ακόμη μια παρατήρηση για την πρώτη άσκηση
Θεώρημα: Έστω ένα παιγνίδι με δύο παίκτες οι οποίοι κινούνται εναλλάξ. Έστω ότι όπως και να παίξουν, το παιγνίδι ολοκληρώνεται σε πεπερασμένο αριθμό κινήσεων με κάποιον να είναι νικητής (δεν υπάρχει ισοπαλία). Έστω επίσης ότι κάθε παίκτης, σε κάθε του κίνηση, έχει πεπερασμένο αριθμό επιλογών όπου οι επιλογές του εξαρτώνται μόνο από τις προηγούμενες κινήσεις των δύο παικτών. Τότε ένας από τους δύο παίκτες έχει στρατηγική νίκης.
Είναι άμεσο ότι το παιγνίδι της άσκησης 1 ικανοποιεί τα κριτήρια του θεωρήματος και άρα μας λέει ότι κάποιος από τους δύο παίκτες έχει στρατηγική νίκης. (Δεν μας λέει ποιος αλλά η άσκηση δεν το ζητάει.)
Θα δώσω μια απόδειξη του θεωρήματος στην περίπτωση που υπάρχει ένας αριθμός

ώστε το παιγνίδι σίγουρα να τελειώνει μετά από

κινήσεις. Αυτό αν και δεν είναι προφανές (πείστε τον εαυτό σας ότι πράγματι δεν είναι προφανές) έπεται από τις συνθήκες του θεωρήματος. Δεν θα δώσω απόδειξη για αυτό. Για την άσκηση 1 βέβαια είναι άμεσο ότι είμαστε σε αυτήν την περίπτωση.
Θα ονομάζουμε θέση του παιγνιδιού μια ακολουθία

κινήσεων, όπου το
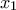
είναι μια κίνηση του πρώτου παίκτη,

είναι μια κίνηση του δεύτερου παίκτη η οποία επιτρέπεται να γίνει αν ο πρώτος παίκτης έκανε την κίνηση
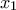
κ.τ.λ. Θα ονομάζουμε επίσης μια θέση

τελική αν μετά την κίνηση

δεν επιτρέπεται να γίνουν άλλες κινήσεις. Παρατηρούμε ότι από τις συνθήκες του θεωρήματος υπάρχει πεπερασμένος αριθμός θέσεων και επιπλέον κάθε θέση έχει το πολύ

κινήσεις. Σκοπός μας είναι να δώσουμε τιμές 1 ή 2 σε όλες τις θέσεις έτσι ώστε αν το παιγνίδι αρχίσει από την συγκεκριμένη θέση (φυσικά αν η συγκεκριμένη θέση προκύψει μετά από περιττό αριθμό κινήσεων τότε στο παιγνίδι που ξεκινάει από αυτήν την θέση παίζει πρώτος ο δεύτερος παίκτης) τότε αν η τιμή είναι 1 θα έχει στρατηγική νίκης ο πρώτος παίκτης ενώ αν είναι 2 ο δεύτερος.
Θα προχωρήσουμε επαγωγικά αλλά ανάποδα. Κοιτάζουμε πρώτα όλες τις θέσεις με

κινήσεις. Από τις συνθήκες είναι όλες του τελικές και σε κάθε μία από αυτή δίνουμε την τιμή 1 ή 2 ανάλογα αν σε αυτήν την τελική θέση νικητής είναι ο πρώτος παίκτης ή ο δεύτερος. Έστω ότι έχουμε δώσει τιμές 1,2 σε όλες τις θέσεις με περισσότερες από

κινήσεις ώστε να ικανοποιούνται οι συνθήκες. Θα δείξουμε τώρα πως θα δώσουμε τιμές για τις θέσεις με

κινήσεις. Ας πάρουμε πρώτα την περίπτωση ο

να είναι άρτιος. Δηλαδή από όλες αυτές συνεχίζει ο πρώτος παίκτης. Τότε για την θέση

(α) Αν η θέση είναι τελική, τότε της δίνουμε την τιμή αυτού που κέρδισε.
(β) Αν δεν είναι τελική και υπάρχει

ώστε η θέση
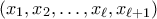
να έχει την τιμή 1, τότε της δίνουμε την τιμή 1.
(γ) Αλλιώς τις δίνουμε την τιμή 2.
Αν έχουμε δώσει στην θέση την τιμή 1 τότε είτε έχει ήδη κερδίσει ο πρώτος παίκτης (περίπτωση (α)) είτε είμαστε στην περίπτωση (β) οπότε ο πρώτος παίκτης μπορεί να κερδίσει παίζοντας την κίνηση

. Αν της δώσαμε την τιμή 2, τότε είτε έχει ήδη κερδίσει ο πρώτος παίκτης, είτε είμαστε στην περίπτωση (γ) οπότε όπως και να παίξει ο πρώτος παίκτης θα καταλήξει σε μια θέση με

κινήσεις που θα έχει την τιμή 2 οπότε ο δεύτερος παίκτης έχει στρατηγική νίκης.
Ομοίως εργαζόμαστε αν ο

είναι περιττός οπότε η απόδειξη του θεωρήματος έχει ολοκληρωθεί.
Αυτή η μέθοδος μπορεί να χρησιμοποιηθεί για να βρεθεί μια στρατηγική νίκης. Μόνο που δεν είναι
καθόλου πρακτική. Ήδη για την πρώτη κίνηση του πρώτου παίκτη έχουμε

διαφορετικές επιλογές/θέσεις. Για κάθε μία από αυτές θα πρέπει να βρούμε την τιμή της και για να το κάνουμε αυτό πρέπει πρώτα να βρούμε τις τιμές όλων των θέσεων που την ακολουθούν κ.τ.λ.
 είναι εγγεγραμμένο σε ένα τετράγωνο
είναι εγγεγραμμένο σε ένα τετράγωνο 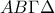 ώστε οι κορυφές του
ώστε οι κορυφές του  να βρίσκονται πάνω στις πλευρές
να βρίσκονται πάνω στις πλευρές  ,
,  ,
, 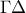 , και
, και  αντίστοιχα. Αν ο λόγος του εμβαδού του
αντίστοιχα. Αν ο λόγος του εμβαδού του  προς το εμβαδόν του
προς το εμβαδόν του  είναι
είναι  , να βρείτε το λόγο των μηκών των τμημάτων στα οποία διαιρούνται οι πλευρές του τετραγώνου
, να βρείτε το λόγο των μηκών των τμημάτων στα οποία διαιρούνται οι πλευρές του τετραγώνου  από τις κορυφές του άλλου τετραγώνου.
από τις κορυφές του άλλου τετραγώνου.  ,
,  να αποδείξετε ότι
να αποδείξετε ότι  .
.


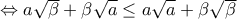
 \displaystyle{(\beta -a)}
\displaystyle{(\beta -a)}
 (1)
(1) αφού
αφού  , όμοια
, όμοια 



 η (1) ισχύει ως ισότητα.
η (1) ισχύει ως ισότητα.

 τα μήκη των πλευρών του. Επειδή οι
τα μήκη των πλευρών του. Επειδή οι  , πρέπει οι και οι τρεις να είναι περιττοί, ή μόνο ο ένας να είναι περιττός. Από των τύπο του Ήρωνα το εμβαδόν του τριγώνου ισούται με
, πρέπει οι και οι τρεις να είναι περιττοί, ή μόνο ο ένας να είναι περιττός. Από των τύπο του Ήρωνα το εμβαδόν του τριγώνου ισούται με  και από την προηγούμενη παρατήρηση βλέπουμε ότι οι
και από την προηγούμενη παρατήρηση βλέπουμε ότι οι  είναι όλοι περιττοί και άρα
είναι όλοι περιττοί και άρα  για κάποιο περιττό ακέραιο
για κάποιο περιττό ακέραιο  . Αν όμως π.χ. το ύψος
. Αν όμως π.χ. το ύψος  είναι ακέραιος τότε έχουμε επίσης ότι
είναι ακέραιος τότε έχουμε επίσης ότι  για κάποιο ακέραιο
για κάποιο ακέραιο  . Αλλά τότε παίρνουμε
. Αλλά τότε παίρνουμε  και άρα
και άρα  , δηλαδή ο
, δηλαδή ο 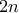 άρα υπάρχουν δύο κορυφές
άρα υπάρχουν δύο κορυφές  ώστε η
ώστε η  να αφήνει τα
να αφήνει τα  σημεία στο ένα ημιεπίπεδο και τα υπόλοιπα
σημεία στο ένα ημιεπίπεδο και τα υπόλοιπα  , η
, η  γράφεται:
γράφεται: δηλαδή
δηλαδή που ισχύει.
που ισχύει. και
και  κορυφές αντίστοιχα ώστε
κορυφές αντίστοιχα ώστε  . Μετά λοιπόν από την πρώτη κίνηση του πρώτου παίκτη έχουμε δυο κυρτά πολύγωνα με άθροισμα κορυφών
. Μετά λοιπόν από την πρώτη κίνηση του πρώτου παίκτη έχουμε δυο κυρτά πολύγωνα με άθροισμα κορυφών  . Μετά την πρώτη κίνηση του δεύτερου παίκτη θα έχουμε τρία κυρτά πολύγωνα με άθροισμα κορυφών
. Μετά την πρώτη κίνηση του δεύτερου παίκτη θα έχουμε τρία κυρτά πολύγωνα με άθροισμα κορυφών  και γενικά αν το παιγνίδι ολοκληρωθεί μετά από
και γενικά αν το παιγνίδι ολοκληρωθεί μετά από  κινήσεις, θα έχουμε
κινήσεις, θα έχουμε  κυρτά πολύγωνα με άθροισμα κορυφών
κυρτά πολύγωνα με άθροισμα κορυφών  . Όμως το παιγνίδι θα ολοκληρωθεί μόνο όταν όλα τα πολύγωνα γίνουν τρίγωνα. Τότε όμως θα έχουν άθροισμα κορυφών
. Όμως το παιγνίδι θα ολοκληρωθεί μόνο όταν όλα τα πολύγωνα γίνουν τρίγωνα. Τότε όμως θα έχουν άθροισμα κορυφών  και επομένως θα έχουμε
και επομένως θα έχουμε  και άρα
και άρα  . Δηλαδή όπως και να παίξουν το παιγνίδι θα ολοκληρωθεί μετά από
. Δηλαδή όπως και να παίξουν το παιγνίδι θα ολοκληρωθεί μετά από 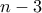 κινήσεις.
κινήσεις. κινήσεων, όπου το
κινήσεων, όπου το 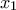 είναι μια κίνηση του πρώτου παίκτη,
είναι μια κίνηση του πρώτου παίκτη,  είναι μια κίνηση του δεύτερου παίκτη η οποία επιτρέπεται να γίνει αν ο πρώτος παίκτης έκανε την κίνηση
είναι μια κίνηση του δεύτερου παίκτη η οποία επιτρέπεται να γίνει αν ο πρώτος παίκτης έκανε την κίνηση  δεν επιτρέπεται να γίνουν άλλες κινήσεις. Παρατηρούμε ότι από τις συνθήκες του θεωρήματος υπάρχει πεπερασμένος αριθμός θέσεων και επιπλέον κάθε θέση έχει το πολύ
δεν επιτρέπεται να γίνουν άλλες κινήσεις. Παρατηρούμε ότι από τις συνθήκες του θεωρήματος υπάρχει πεπερασμένος αριθμός θέσεων και επιπλέον κάθε θέση έχει το πολύ  κινήσεις ώστε να ικανοποιούνται οι συνθήκες. Θα δείξουμε τώρα πως θα δώσουμε τιμές για τις θέσεις με
κινήσεις ώστε να ικανοποιούνται οι συνθήκες. Θα δείξουμε τώρα πως θα δώσουμε τιμές για τις θέσεις με 
 ώστε η θέση
ώστε η θέση 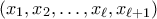 να έχει την τιμή 1, τότε της δίνουμε την τιμή 1.
να έχει την τιμή 1, τότε της δίνουμε την τιμή 1. κινήσεις που θα έχει την τιμή 2 οπότε ο δεύτερος παίκτης έχει στρατηγική νίκης.
κινήσεις που θα έχει την τιμή 2 οπότε ο δεύτερος παίκτης έχει στρατηγική νίκης. διαφορετικές επιλογές/θέσεις. Για κάθε μία από αυτές θα πρέπει να βρούμε την τιμή της και για να το κάνουμε αυτό πρέπει πρώτα να βρούμε τις τιμές όλων των θέσεων που την ακολουθούν κ.τ.λ.
διαφορετικές επιλογές/θέσεις. Για κάθε μία από αυτές θα πρέπει να βρούμε την τιμή της και για να το κάνουμε αυτό πρέπει πρώτα να βρούμε τις τιμές όλων των θέσεων που την ακολουθούν κ.τ.λ. να βρίσκονται πάνω στις πλευρές
να βρίσκονται πάνω στις πλευρές  η πλευρά του
η πλευρά του  η πλευρά του
η πλευρά του  . Τότε
. Τότε  .
. όπου
όπου  . Από το Πυθαγόρειο θεώρημα π.χ. στο
. Από το Πυθαγόρειο θεώρημα π.χ. στο  παίρνουμε
παίρνουμε  .
. και διαιρώντας την τελευταία με τη
και διαιρώντας την τελευταία με τη  κατά μέλη παίρνουμε:
κατά μέλη παίρνουμε: δηλαδή
δηλαδή 
 τότε η παραπάνω γίνεται:
τότε η παραπάνω γίνεται: και η δευτεροβάθμια ως προς
και η δευτεροβάθμια ως προς  που προκύπτει δίνει θετική λύση
που προκύπτει δίνει θετική λύση 

