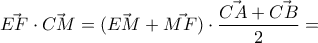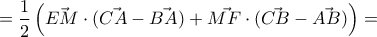Demetres έγραψε:Δίνεται ένας

πίνακας αποτελούμενος από

μοναδιαία τετράγωνα, ένας θετικός ακέραιος

και απεριόριστος αριθμός

-σχημάτων οποιουδήποτε τύπου. Δυο παίκτες, ο

και ο

παίζουν το ακόλουθο παιγνίδι:
Ξεκινώντας με τον

, σημειώνουν εναλλάξ σε κάθε κίνησή τους ένα τετράγωνο που δεν είναι ήδη σημειωμένο, μέχρι να σημειώσουν συνολικά

μοναδιαία τετράγωνα. Μια τοποθέτηση

-σχημάτων λέγεται «καλή» αν τα

-σχήματα δεν επικαλύπτονται και καθένα από αυτά καλύπτει ακριβώς τρία μοναδιαία τετράγωνα του πίνακα που δεν είναι σημειωμένα. Ο

κερδίζει αν μετά από οποιαδήποτε καλή τοποθέτηση

-σχημάτων μένουν ακάλυπτα τουλάχιστον τρία μοναδιαία τετράγωνα που δεν είναι σημειωμένα.
Προσδιορίστε την ελάχιστη τιμή του

για την οποία ο

έχει στρατηγική νίκης.
Κατ' αρχάς συγχαρητήρια σε όλα τα παιδιά από την Ελλάδα που συμμετείχαν στο διαγωνισμό!Είχαμε για άλλη μια χρονιά πολύ καλή εμφάνιση!
Θα προσπαθήσω να προσεγγίσω και το τελευταίο πρόβλημα.
Θα ήθελα να δω και τη λύση που έχει υπ' όψιν του και ο Δημήτρης που το πρότεινε (μπράβο,και επί τη ευκαιρία,για το πρόβλημα!).

- Συνδυαστική JBMO 2015.PNG (232.54 KiB) Προβλήθηκε 3821 φορές
Θα δείξουμε αρχικά πως για

ο

έχει στρατηγική νίκης.

Αν ο

σημειώσει στην πρώτη κίνηση κάποιο από τα τετράγωνα από τα οποία περνά κάποια κόκκινη γραμμή,τότε ο

παίζει έτσι ώστε στο τέλος των

κινήσεων να υπάρχει κάποια γραμμή ή στήλη από αυτές που αντιστοιχούν σε κόκκινες γραμμές,στην οποία να υπάρχουν

σημειωμένα τετράγωνα.Για παράδειγμα αν ο

σημειώσει το
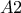
τότε ο

θέλει στο τέλος των κινήσεων να είναι σημειωμένα τα

.Αυτό προφανώς μπορεί να γίνει αφού ο

έχει δύο κινήσεις.
Στην περίπτωση αυτή,είναι εμφανές ότι τα

δεν μπορούν να καλυφθούν σε κάποια καλή τοποθέτηση.Ακόμη κι αν ο

στην δεύτερη κίνησή του καλύψει ένα από αυτά,τότε μένει ένα ακάλυπτο.Δεδομένου ότι σε κάθε καλή τοποθέτηση το πλήθος των καλυμμένων τετραγώνων είναι πολλαπλάσιο του

,και πως μετά τις

κινήσεις μένουν

μη σημειωμένα τετράγωνα,τότε αφού

από αυτά θα μείνει οπωσδήποτε ακάλυπτο,θα καλυφθούν το πολύ

τετράγωνα και ο

θα κερδίσει (ομοίως,αν π.χ. ο

σημειώσει το

τότε ο

φροντίζει ώστε να σημειωθούν τα

ή τα

και τότε θα έχει κερδίσει όπως περιγράψαμε παραπάνω).

Αν ο

σημειώσει στην αρχή ένα γωνιακό τετράγωνο τότε ο

σημειώνει το τετράγωνο που μοιράζεται μόνο μία κορυφή με αυτό που σημείωσε ο

(αν π.χ. ο

σημειώσει το

τότε ο

σημειώνει το

).Όποια και να είναι η επόμενη κίνηση του

ο

μπορεί να "εγκλωβίσει" ένα από τα γειτονικά τετράγωνα του γωνιακού (στο προηγούμενο παράδειγμα δηλαδή,ένα εκ των

).Αυτό μπορεί να το κάνει ως εξής:αν ο

στη δεύτερη κίνηση δε σημειώσει το

τότε ο

σημειώνει το

κι έτσι "εγκλωβίζει" το

,αλλιώς σημειώνει το

και "εγκλωβίζει" το
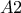
.Λόγω του επιχειρήματος με τα πολλαπλάσια του

θα κερδίσει και πάλι.

Αν ο

σημειώσει στην αρχή κάποιο εκ των

τότε ο

μπορεί να φροντίσει ώστε να σημειωθούν αντίστοιχα τα ζεύγη

και τότε θα έχουν "εγκλωβιστεί" σε κάθε περίπτωση δύο τετράγωνα που βρίσκονται στην περιφέρεια του πίνακα.Ακόμη κι αν ο

σημειώσει στη δεύτερη κίνηση κάποιο από αυτά,τότε μένει ένα που δεν μπορεί να καλυφθεί από καλή τοποθέτηση,και με βάση το επιχείρημα με τα πολλαπλάσια του

ο

κερδίζει και πάλι.

Αν ο

σημειώσει στην πρώτη κίνηση το

,τότε ο

σημειώνει το

.Αν ο

δε σημειώσει στη δεύτερη κίνησή του το

τότε ο

σημειώνει το
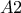
και το

"εγκλωβίζεται" όποτε ο

κερδίζει όπως και στις προηγούμενες περιπτώσεις.Έστω ότι ο

σημειώνει και το

.Ο

μετά μπορεί να σημειώσει το

.Μετά,υπάρχουν

τρόποι να καλυφθεί το
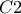
σε μια καλή τοποθέτηση.Ο πρώτος είναι με το

που καλύπτει τα

.Τότε το

δεν μπορεί να καλυφθεί και ο

κερδίζει.Ο άλλος τρόπος είναι να χρησιμοποιηθεί το

που καλύπτει τα

.Τότε αναγκαστικά θα χρησιμοποιηθεί και το

που καλύπτει τα

.Τώρα πια για να καλυφθεί το

πρέπει να χρησιμοποιηθεί το

που καλύπτει τα

.Όμως τότε το

δεν μπορεί να καλυφθεί άρα ο

κερδίζει.Τέλος,μπορεί να χρησιμοποιηθεί το

που καλύπτει τα

.Τότε όμως δεν μπορεί να καλυφθεί το
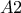
οπότε ο

και πάλι κερδίζει.
Επομένως σε κάθε περίπτωση ο

μπορεί να κερδίσει αν

.
Μένει να δείξουμε πως ο

δεν έχει την τύχη στα χέρια του αν

.Για
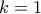
αυτό είναι προφανές.Θα εξετάσουμε τώρα την περίπτωση

.Υποθέτουμε ότι αρχικά ο

σημειώνει το κεντρικό τετράγωνο.Λόγω συμμετρίας υπάρχουν

περιπτώσεις:
1. Ο

επιλέγει ένα εκ των

.
2. Ο

επιλέγει το

.
3. Ο

επιλέγει ένα εκ των

.
Όλες οι άλλες περιπτώσεις ανάγονται σε αυτές τις

.Για κάθε μια εύκολα βλέπουμε πως υπάρχει καλή τοποθέτηση ώστε να κερδίζει ο

(για να μην εξετάζετε πολλές περιπτώσεις ψάξτε π.χ. για καλή τοποθέτηση που αφήνει ακάλυπτα τα

μαζί ώστε να καλύψετε μαζί τις περιπτώσεις όπου ο

επιλέγει κάποιο από αυτά).
Η περίπτωση

απορρίπτεται εύκολα.Στην προηγούμενη περίπτωση ο,τι και να επιλέξει ο

υπάρχει καλή τοποθέτηση ώστε να κερδίζει ο

.Όμως σε κάθε τέτοια καλή τοποθέτηση μένουν

τετράγωνα κενά.Ο

λοιπόν μετά την κίνηση του

έχει δύο (τουλάχιστον) πιθανές επιλογές ώστε να κερδίσει.
 και όλους τους θετικούς ακεραίους
και όλους τους θετικούς ακεραίους  που ικανοποιούν την εξίσωση
που ικανοποιούν την εξίσωση 
 που είναι τέτοιοι ώστε
που είναι τέτοιοι ώστε  . Βρείτε την ελάχιστη τιμή της παράστασης
. Βρείτε την ελάχιστη τιμή της παράστασης
 . Οι ευθείες
. Οι ευθείες  και
και  είναι κάθετες στην
είναι κάθετες στην  στα σημεία
στα σημεία  και
και  αντίστοιχα. Οι κάθετες ευθείες από το μέσον
αντίστοιχα. Οι κάθετες ευθείες από το μέσον  του
του  προς τις πλευρές
προς τις πλευρές  και
και  του τριγώνου τέμνουν τις ευθείες
του τριγώνου τέμνουν τις ευθείες  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Αν
αντίστοιχα. Αν  είναι το σημείο τομής των ευθειών
είναι το σημείο τομής των ευθειών  και
και 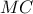 , να αποδείξετε ότι
, να αποδείξετε ότι 
 -σχήμα.
-σχήμα. πίνακας αποτελούμενος από
πίνακας αποτελούμενος από  μοναδιαία τετράγωνα, ένας θετικός ακέραιος
μοναδιαία τετράγωνα, ένας θετικός ακέραιος  και απεριόριστος αριθμός
και απεριόριστος αριθμός  -σχημάτων οποιουδήποτε τύπου. Δυο παίκτες, ο
-σχημάτων οποιουδήποτε τύπου. Δυο παίκτες, ο  και ο
και ο  παίζουν το ακόλουθο παιγνίδι:
παίζουν το ακόλουθο παιγνίδι: , σημειώνουν εναλλάξ σε κάθε κίνησή τους ένα τετράγωνο που δεν είναι ήδη σημειωμένο, μέχρι να σημειώσουν συνολικά
, σημειώνουν εναλλάξ σε κάθε κίνησή τους ένα τετράγωνο που δεν είναι ήδη σημειωμένο, μέχρι να σημειώσουν συνολικά  μοναδιαία τετράγωνα. Μια τοποθέτηση
μοναδιαία τετράγωνα. Μια τοποθέτηση  -σχημάτων λέγεται «καλή» αν τα
-σχημάτων λέγεται «καλή» αν τα  -σχήματα δεν επικαλύπτονται και καθένα από αυτά καλύπτει ακριβώς τρία μοναδιαία τετράγωνα του πίνακα που δεν είναι σημειωμένα. Ο
-σχήματα δεν επικαλύπτονται και καθένα από αυτά καλύπτει ακριβώς τρία μοναδιαία τετράγωνα του πίνακα που δεν είναι σημειωμένα. Ο  κερδίζει αν μετά από οποιαδήποτε καλή τοποθέτηση
κερδίζει αν μετά από οποιαδήποτε καλή τοποθέτηση  -σχημάτων μένουν ακάλυπτα τουλάχιστον τρία μοναδιαία τετράγωνα που δεν είναι σημειωμένα.
-σχημάτων μένουν ακάλυπτα τουλάχιστον τρία μοναδιαία τετράγωνα που δεν είναι σημειωμένα.  για την οποία ο
για την οποία ο  έχει στρατηγική νίκης.
έχει στρατηγική νίκης.
 με ισότητα αν-ν
με ισότητα αν-ν 
 και κάνοντας πράξεις φτάνουμε στην
και κάνοντας πράξεις φτάνουμε στην 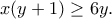
 και
και  οπότε
οπότε 
 .Δεδομένου ότι
.Δεδομένου ότι  ,ακριβώς δύο από τους
,ακριβώς δύο από τους  θα διαιρούνται με το
θα διαιρούνται με το  .
. στην αρχική εξίσωση,μπορούμε να θεωρήσουμε
στην αρχική εξίσωση,μπορούμε να θεωρήσουμε  περιπτώσεις.
περιπτώσεις. Έστω ότι
Έστω ότι  .Λόγω του ότι το
.Λόγω του ότι το  .
.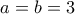 .Επομένως η αρχική γράφεται
.Επομένως η αρχική γράφεται  .
. .Επίσης ισχύει
.Επίσης ισχύει 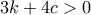 άρα αναγκαστικά
άρα αναγκαστικά 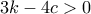 .
. και
και  .Το σύστημα αυτό έχει λύση την
.Το σύστημα αυτό έχει λύση την  που είναι δεκτή.
που είναι δεκτή. .
. .Τότε ισχύει
.Τότε ισχύει  κι επειδή οι
κι επειδή οι  είναι πρώτοι συμπεραίνουμε ότι
είναι πρώτοι συμπεραίνουμε ότι 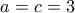 .
. .
. κι επειδή οι δύο αυτοί όροι είναι αναγκαστικά και οι δύο άρτιοι,υπάρχουν οι εξής περιπτώσεις:
κι επειδή οι δύο αυτοί όροι είναι αναγκαστικά και οι δύο άρτιοι,υπάρχουν οι εξής περιπτώσεις: που είναι δεκτή.
που είναι δεκτή. που είναι επίσης δεκτή.
που είναι επίσης δεκτή. .
.
 έχουν την ίδια αρτιοπεριττότητα.Είναι αδύνατο να είναι κι οι δύο περιττοί άρα είναι κι οι δύο άρτιοι.
έχουν την ίδια αρτιοπεριττότητα.Είναι αδύνατο να είναι κι οι δύο περιττοί άρα είναι κι οι δύο άρτιοι.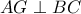 και
και  με
με  και
και  .
. .Θα χρησιμοποιήσουμε διανύσματα.Ως γνωστόν
.Θα χρησιμοποιήσουμε διανύσματα.Ως γνωστόν  .
. .Συνεπώς
.Συνεπώς  .
. λόγω των καθετοτήτων.Άρα
λόγω των καθετοτήτων.Άρα  .
. θα ισχύει
θα ισχύει 

 και τέλος.
και τέλος. άρα το
άρα το 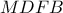 είναι εγγράψιμο.
είναι εγγράψιμο. άρα και το
άρα και το  είναι εγγράψιμο.
είναι εγγράψιμο. και
και  άρα
άρα  και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε. είναι το σημείο τομής των
είναι το σημείο τομής των  και
και  το κοινό σημείο των
το κοινό σημείο των  έχουμε
έχουμε  δηλαδή το
δηλαδή το  είναι εγγράψιμο. Άρα χρησιμοποιώντας και το εγγράψιμο
είναι εγγράψιμο. Άρα χρησιμοποιώντας και το εγγράψιμο  είναι:
είναι:  άρα το
άρα το  είναι επίσης εγγράψιμο, οπότε η γωνία
είναι επίσης εγγράψιμο, οπότε η γωνία  , από το οποίο έπεται εύκολα το ζητούμενο όπως στη λύση παραπάνω του gavrilos.
, από το οποίο έπεται εύκολα το ζητούμενο όπως στη λύση παραπάνω του gavrilos. ο
ο  έχει στρατηγική νίκης.
έχει στρατηγική νίκης. σημειώσει στην πρώτη κίνηση κάποιο από τα τετράγωνα από τα οποία περνά κάποια κόκκινη γραμμή,τότε ο
σημειώσει στην πρώτη κίνηση κάποιο από τα τετράγωνα από τα οποία περνά κάποια κόκκινη γραμμή,τότε ο  κινήσεων να υπάρχει κάποια γραμμή ή στήλη από αυτές που αντιστοιχούν σε κόκκινες γραμμές,στην οποία να υπάρχουν
κινήσεων να υπάρχει κάποια γραμμή ή στήλη από αυτές που αντιστοιχούν σε κόκκινες γραμμές,στην οποία να υπάρχουν  τότε ο
τότε ο  .Αυτό προφανώς μπορεί να γίνει αφού ο
.Αυτό προφανώς μπορεί να γίνει αφού ο  δεν μπορούν να καλυφθούν σε κάποια καλή τοποθέτηση.Ακόμη κι αν ο
δεν μπορούν να καλυφθούν σε κάποια καλή τοποθέτηση.Ακόμη κι αν ο  μη σημειωμένα τετράγωνα,τότε αφού
μη σημειωμένα τετράγωνα,τότε αφού  από αυτά θα μείνει οπωσδήποτε ακάλυπτο,θα καλυφθούν το πολύ
από αυτά θα μείνει οπωσδήποτε ακάλυπτο,θα καλυφθούν το πολύ  τετράγωνα και ο
τετράγωνα και ο  τότε ο
τότε ο  ή τα
ή τα  και τότε θα έχει κερδίσει όπως περιγράψαμε παραπάνω).
και τότε θα έχει κερδίσει όπως περιγράψαμε παραπάνω). τότε ο
τότε ο  ).Όποια και να είναι η επόμενη κίνηση του
).Όποια και να είναι η επόμενη κίνηση του  ).Αυτό μπορεί να το κάνει ως εξής:αν ο
).Αυτό μπορεί να το κάνει ως εξής:αν ο  τότε ο
τότε ο  κι έτσι "εγκλωβίζει" το
κι έτσι "εγκλωβίζει" το  και "εγκλωβίζει" το
και "εγκλωβίζει" το  τότε ο
τότε ο  και τότε θα έχουν "εγκλωβιστεί" σε κάθε περίπτωση δύο τετράγωνα που βρίσκονται στην περιφέρεια του πίνακα.Ακόμη κι αν ο
και τότε θα έχουν "εγκλωβιστεί" σε κάθε περίπτωση δύο τετράγωνα που βρίσκονται στην περιφέρεια του πίνακα.Ακόμη κι αν ο  ,τότε ο
,τότε ο  σε μια καλή τοποθέτηση.Ο πρώτος είναι με το
σε μια καλή τοποθέτηση.Ο πρώτος είναι με το  που καλύπτει τα
που καλύπτει τα  .Τότε το
.Τότε το  δεν μπορεί να καλυφθεί και ο
δεν μπορεί να καλυφθεί και ο  .Τότε αναγκαστικά θα χρησιμοποιηθεί και το
.Τότε αναγκαστικά θα χρησιμοποιηθεί και το  .Τώρα πια για να καλυφθεί το
.Τώρα πια για να καλυφθεί το  πρέπει να χρησιμοποιηθεί το
πρέπει να χρησιμοποιηθεί το  .Όμως τότε το
.Όμως τότε το  δεν μπορεί να καλυφθεί άρα ο
δεν μπορεί να καλυφθεί άρα ο  .Τότε όμως δεν μπορεί να καλυφθεί το
.Τότε όμως δεν μπορεί να καλυφθεί το  .Για
.Για 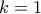 αυτό είναι προφανές.Θα εξετάσουμε τώρα την περίπτωση
αυτό είναι προφανές.Θα εξετάσουμε τώρα την περίπτωση  .Υποθέτουμε ότι αρχικά ο
.Υποθέτουμε ότι αρχικά ο  .
. .
. απορρίπτεται εύκολα.Στην προηγούμενη περίπτωση ο,τι και να επιλέξει ο
απορρίπτεται εύκολα.Στην προηγούμενη περίπτωση ο,τι και να επιλέξει ο  , ο
, ο  , ο
, ο  ο
ο  κερδίζει ο
κερδίζει ο  ασημείωτα τετράγωνα, ο
ασημείωτα τετράγωνα, ο  της πιο κάτω εικόνας.
της πιο κάτω εικόνας.  and
and  ο
ο  . Τότε ο
. Τότε ο  μένει ασημείωτο και δεν μπορεί να καλυφθεί με
μένει ασημείωτο και δεν μπορεί να καλυφθεί με  . Τότε ο
. Τότε ο  ασημείωτα μαύρα τετράγωνα. Κάθε
ασημείωτα μαύρα τετράγωνα. Κάθε 
 τότε ο
τότε ο  και το
και το  και μπλοκάρει το
και μπλοκάρει το  άρα κερδίζει.
άρα κερδίζει. η στην γραμμή
η στην γραμμή  o
o  .Αν το τετραγωνακι είναι στην στήλη
.Αν το τετραγωνακι είναι στην στήλη  ο
ο 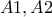 και κερδίζει
και κερδίζει  .O
.O  μπλοκάρεται το
μπλοκάρεται το  και κερδίζει. Αν ο
και κερδίζει. Αν ο  και μπλοκάρεται το
και μπλοκάρεται το  άρα παλι κερδιζει
άρα παλι κερδιζει


 σημαίνει ότι το
σημαίνει ότι το  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  αλλά
αλλά 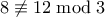 .
. οπότε το
οπότε το 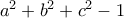 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  μπορώ να αφαιρέσω κάποιο πολλαπλάσιο του
μπορώ να αφαιρέσω κάποιο πολλαπλάσιο του  . Π.χ. αφαιρώντας
. Π.χ. αφαιρώντας  από το αριστερό και
από το αριστερό και  από το δεξί μπορώ να γράψω απευθείας
από το δεξί μπορώ να γράψω απευθείας  .
. ή
ή 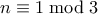 οτιδήποτε και αν είναι το
οτιδήποτε και αν είναι το  .
. ,
,  ,
,  ,
,  .
. ,
,  .
.  ,
,  είναι ίση με αυτή των διανυσμάτων
είναι ίση με αυτή των διανυσμάτων  ,
,  .
. κέντρου
κέντρου 
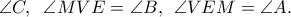 Τότε η ευθεία της διαμέσου
Τότε η ευθεία της διαμέσου  που διέρχεται από το μέσο
που διέρχεται από το μέσο  της
της  θα είναι κάθετη στη διάμεσο
θα είναι κάθετη στη διάμεσο  Οπότε παίρνουμε
Οπότε παίρνουμε  Έτσι οδηγούμαστε στην εγγραψιμμότητα των τετραπλεύρων
Έτσι οδηγούμαστε στην εγγραψιμμότητα των τετραπλεύρων 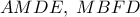 που δίνει αυτόματα την ζητούμενη ισότητα.
που δίνει αυτόματα την ζητούμενη ισότητα. και
και  .
. θα ισχύει ότι:
θα ισχύει ότι:  (1)
(1) θα ισχύει ότι:
θα ισχύει ότι:  (2)
(2)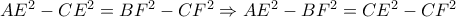 (3)
(3)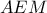 προκύπτει:
προκύπτει:  (4)
(4) προκύπτει:
προκύπτει: 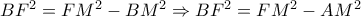 (5)
(5) (6)
(6)
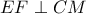 , με διανύσματα :
, με διανύσματα :