1. Το δευτεροβάθμιο τριώνυμο
 είναι τέτοιο, ώστε το πολυώνυμο
είναι τέτοιο, ώστε το πολυώνυμο 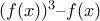 να έχει ακριβώς τρεις πραγματικές ρίζες. Να βρείτε την τεταγμένη της κορυφής του δευτεροβάθμιου τριωνύμου.
να έχει ακριβώς τρεις πραγματικές ρίζες. Να βρείτε την τεταγμένη της κορυφής του δευτεροβάθμιου τριωνύμου.2. Να αποδείξετε ότι μπορεί να βρεθεί φυσικός αριθμός
 , τέτοιος ώστε το γινόμενο κάποιων
, τέτοιος ώστε το γινόμενο κάποιων  διαδοχικών φυσικών αριθμών να είναι ίσο με το γινόμενο κάποιων
διαδοχικών φυσικών αριθμών να είναι ίσο με το γινόμενο κάποιων  διαδοχικών φυσικών αριθμών.
διαδοχικών φυσικών αριθμών.3. Ο Κώστας είχε δυο συλλογές των 17 νομισμάτων η κάθε μία. Στην μία συλλογή όλα τα νομίσματα είναι γνήσια στην άλλη ακριβώς πέντε είναι κάλπικα ( όλα τα νομίσματα οπτικά φαίνονται το ίδιο, όλα τα γνήσια νομίσματα ζυγίζουν το ίδιο, όλα τα κάλπικα νομίσματα ζυγίζουν και αυτά το ίδιο αλλά δεν γνωρίζουμε αν είναι ελαφρύτερα ή βαρύτερα των γνησίων). Μια από τις συλλογές ο Κώστας την έδωσε σε φίλο του, αλλά στη συνέχεια ξέχασε, ποια ακριβώς συλλογή του έμεινε. Μπορεί ο Κώστας με δυο ζυγίσεις σε ζυγό χωρίς σταθμά να αποφανθεί για το ποια συλλογή έδωσε;
4. Οι κύκλοι
 και
και  εφάπτονται εξωτερικά στο σημείο
εφάπτονται εξωτερικά στο σημείο  . Τα σημεία
. Τα σημεία  και
και  του
του  και τα σημεία
και τα σημεία  και
και  του
του  είναι τέτοια, ώστε οι
είναι τέτοια, ώστε οι  και
και  να είναι εξωτερικές εφαπτομένες αυτών. Η ευθεία
να είναι εξωτερικές εφαπτομένες αυτών. Η ευθεία  τέμενει το τμήμα
τέμενει το τμήμα  στο
στο  , και η ευθεία
, και η ευθεία  τέμνει εκ νέου τον
τέμνει εκ νέου τον  στο
στο  . Να δείξετε, ότι τα σημεία
. Να δείξετε, ότι τα σημεία  και
και  είναι συνευθειακά.
είναι συνευθειακά. Δεύτερη Μέρα
5. Ο φυσικός αριθμός
 είναι τέτοιος, ώστε το άθροισμα των ψηφίων στη δεκαδική μορφή του αριθμού
είναι τέτοιος, ώστε το άθροισμα των ψηφίων στη δεκαδική μορφή του αριθμού  να είναι ίσο με
να είναι ίσο με  . Μπορεί σε μία τέτοια περίπτωση το τελευταίο ψηφίο του
. Μπορεί σε μία τέτοια περίπτωση το τελευταίο ψηφίο του  να είναι ίσο με
να είναι ίσο με  ;
;6. Ο εγγεγραμμένος κύκλος
 του τριγώνου
του τριγώνου  εφάπτεται των πλευρών
εφάπτεται των πλευρών  στα σημεία
στα σημεία  και
και  αντίστοιχα. Στην ευθεία
αντίστοιχα. Στην ευθεία  προς το μέρος του
προς το μέρος του  διαλέγουμε σημείο
διαλέγουμε σημείο  τέτοιο ώστε
τέτοιο ώστε 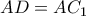 . Οι ευθείες
. Οι ευθείες  και
και 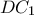 τέμνουν εκ νέου τον
τέμνουν εκ νέου τον  στα σημεία
στα σημεία  και
και  . Να αποδείξετε ότι το
. Να αποδείξετε ότι το  είναι διάμετρος του
είναι διάμετρος του  .
.7. Οι θετικοί αριθμοί
 ικανοποιούν τις εξισώσεις
ικανοποιούν τις εξισώσεις 

Να δείξετε ότι οι αριθμοί
 είναι ίσοι μεταξύ τους.
είναι ίσοι μεταξύ τους.8. Σε ένα πάρτι μία ομάδα των 20 ατόμων ζητείται να καθίσει σε 4 τραπέζια. Ένας τρόπος καθίσματος ονομάζεται επιτυχής, αν οποιαδήποτε δύο άτομα που θα καθίσουν στο ίδιο τραπέζι, είναι φίλοι. Αποφάνθηκε ότι επιτυχείς τρόποι καθίσματος υπάρχουν, και μάλιστα σε κάθε επιτυχή τρόπο καθίσματος σε κάθε τραπέζι κάθονται ακριβώς 5 άτομα. Ποιος είναι ο μέγιστος αριθμός από ζεύγη φίλων σε αυτή την ομάδα.

 των
των 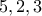 και
και  νομισμάτων αντίστοιχα.
νομισμάτων αντίστοιχα.  . Αν δεν ισορροπούν τότε έχουμε τα κάλπικα.
. Αν δεν ισορροπούν τότε έχουμε τα κάλπικα.  έχουν από
έχουν από  ή
ή  ή
ή  κάλπικα.
κάλπικα. και στον άλλο τα
και στον άλλο τα  κάλπικα στον πρώτο ζυγό και
κάλπικα στον πρώτο ζυγό και  στον δεύτερο οπότε δεν θα έχουμε ισορροπία.
στον δεύτερο οπότε δεν θα έχουμε ισορροπία. κάλπικα στον πρώτο ζυγό και
κάλπικα στον πρώτο ζυγό και  στον δεύτερο οπότε δεν θα έχουμε ισορροπία.
στον δεύτερο οπότε δεν θα έχουμε ισορροπία. στον δεύτερο οπότε πάλι δεν θα έχουμε ισορροπία.
στον δεύτερο οπότε πάλι δεν θα έχουμε ισορροπία.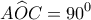 και επειδή
και επειδή  , η
, η  , οπότε
, οπότε  .
. , οπότε η
, οπότε η  είναι διάμετρος του κύκλου
είναι διάμετρος του κύκλου  και κατά συνέπεια
και κατά συνέπεια  . Αλλά,
. Αλλά,  , άρα
, άρα  .
. το σημείο τομής των
το σημείο τομής των  . Είναι:
. Είναι:  και
και  . Άρα τα τρίγωνα
. Άρα τα τρίγωνα  είναι ισογώνια,
είναι ισογώνια,  . Ομοίως είναι
. Ομοίως είναι 
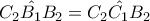 , ως εγγεγραμμένες στο ίδιο τόξο, άρα
, ως εγγεγραμμένες στο ίδιο τόξο, άρα  και το ζητούμενο έπεται άμεσα.
και το ζητούμενο έπεται άμεσα. . Τότε όμως
. Τότε όμως  και άρα το άθροισμα των ψηφίων του
και άρα το άθροισμα των ψηφίων του  είναι ισότιμο με
είναι ισότιμο με  . Άρα το άθροισμα των ψηφίων δεν μπορεί να είναι
. Άρα το άθροισμα των ψηφίων δεν μπορεί να είναι 

 η διακρίνουσα του
η διακρίνουσα του ,
, η διακρίνουσα του
η διακρίνουσα του  ,
, η διακρίνουσα του
η διακρίνουσα του 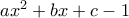

 τότε
τότε 
 έχει το πολύ 2 ρίζες που είναι του πολ/μου
έχει το πολύ 2 ρίζες που είναι του πολ/μου τότε
τότε 
 ρίζα του πρώτου θα είναι
ρίζα του πρώτου θα είναι  )
) τότε
τότε  και
και 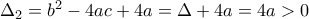

 ζεύγη αν τους χωρίσουμε σε πέντε ομάδες
ζεύγη αν τους χωρίσουμε σε πέντε ομάδες  των τεσσάρων ατόμων η κάθε μία, με δύο άτομα να είναι φίλοι αν και μόνο αν ανήκουν σε διαφορετικές ομάδες: Συνολικά έχουμε
των τεσσάρων ατόμων η κάθε μία, με δύο άτομα να είναι φίλοι αν και μόνο αν ανήκουν σε διαφορετικές ομάδες: Συνολικά έχουμε  ζεύγη φίλων. Μπορούμε εύκολα να τους καθίσουμε επιτυχώς αν σε κάθε τραπέζι βάλουμε ένα άτομο από κάθε ομάδα. Σε κάθε επιτυχή τρόπο καθίσματος έχουμε όντως 5 άτομα σε κάθε τραπέζι αφού αλλιώτικα θα υπήρχε τραπέζι στο οποίο θα κάθονταν τουλάχιστον 6 άτομα, κάτι που οδηγεί σε άτοπο αφού τότε δυο άτομα θα ήταν από την ίδια ομάδα.
ζεύγη φίλων. Μπορούμε εύκολα να τους καθίσουμε επιτυχώς αν σε κάθε τραπέζι βάλουμε ένα άτομο από κάθε ομάδα. Σε κάθε επιτυχή τρόπο καθίσματος έχουμε όντως 5 άτομα σε κάθε τραπέζι αφού αλλιώτικα θα υπήρχε τραπέζι στο οποίο θα κάθονταν τουλάχιστον 6 άτομα, κάτι που οδηγεί σε άτοπο αφού τότε δυο άτομα θα ήταν από την ίδια ομάδα. τα σύνολα των ατόμων που κάθονται στα τέσσερα τραπέζια. Αν σηκώσω κάποιο άτομο από ένα τραπέζι και τον κάτσω σε άλλο τραπέζι, τότε δεν θα έχω επιτυχή τρόπο καθίσματος. Για να συμβαίνει αυτό πρέπει αυτό το άτομο να έχει τουλάχιστον ένα μη φίλο στο άλλο τραπέζι.
τα σύνολα των ατόμων που κάθονται στα τέσσερα τραπέζια. Αν σηκώσω κάποιο άτομο από ένα τραπέζι και τον κάτσω σε άλλο τραπέζι, τότε δεν θα έχω επιτυχή τρόπο καθίσματος. Για να συμβαίνει αυτό πρέπει αυτό το άτομο να έχει τουλάχιστον ένα μη φίλο στο άλλο τραπέζι.  και κάθε τραπέζι στο οποίο δεν κάθεται ο
και κάθε τραπέζι στο οποίο δεν κάθεται ο  ώστε οι
ώστε οι  ζεύγη μη φίλων. (Διαιρούμε με το δύο για την διπλομέτρηση.) Αν όμως υπάρχουν τουλάχιστον
ζεύγη μη φίλων. (Διαιρούμε με το δύο για την διπλομέτρηση.) Αν όμως υπάρχουν τουλάχιστον  ζεύγη μη φίλων τότε υπάρχουν το πολύ
ζεύγη μη φίλων τότε υπάρχουν το πολύ  ζεύγη φίλων.
ζεύγη φίλων. δίνει
δίνει 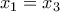 ή
ή  . Ομοίως παίρνουμε
. Ομοίως παίρνουμε  ή
ή  για κάθε
για κάθε 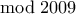 .)
.)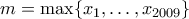 και έστω
και έστω  .
. ώστε
ώστε  . Αφού
. Αφού 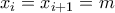 και
και  τότε δεν μπορούμε να έχουμε
τότε δεν μπορούμε να έχουμε  . Άρα πρέπει
. Άρα πρέπει  και άρα
και άρα  . Επαγωγικά
. Επαγωγικά 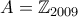 και άρα όλοι οι αριθμοί είναι ίσοι.
και άρα όλοι οι αριθμοί είναι ίσοι.  , αν
, αν 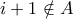 . Έστω
. Έστω  . Τότε
. Τότε 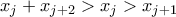 . Δεν μπορούμε λοιπόν να έχουμε
. Δεν μπορούμε λοιπόν να έχουμε  και άρα έχουμε
και άρα έχουμε  . Οπότε
. Οπότε  . Τότε
. Τότε  και επαγωγικά
και επαγωγικά 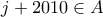 όμως
όμως  . Δηλαδή
. Δηλαδή  , άτοπο.
, άτοπο.
 αρκεί να δείξουμε ότι υπάρχει
αρκεί να δείξουμε ότι υπάρχει 
 .
.