1. Εννιά σκιέρ ξεκίνησαν από την αφετηρία με την σειρά και διήλθαν μια απόσταση ο καθένας με την δική του σταθερή ταχύτητα. Είναι δυνατόν κάθε σκιέρ να συμμετείχε σε ακριβώς τέσσερεις προσπεράσεις; (Σε κάθε προσπέραση συμμετέχουν ακριβώς δυο σκιέρ, αυτός που προσπερνάει και αυτός που προσπεράστηκε.)
2. Είναι δυνατόν για κάποιο φυσικό αριθμό k να χωρίσουμε όλους τους φυσικούς αριθμούς από το 1 έως k σε δυο ομάδες και να γράψουμε τους αριθμούς κάθε ομάδας στη σειρά (κολλητά) με κάποια διάταξη ώστε, να προκύψουν δυο ίσοι αριθμοί;
3. Στο τρίγωνο
 φέρουμε τις διχοτόμους
φέρουμε τις διχοτόμους  και
και  , που τέμνονται στο σημείο
, που τέμνονται στο σημείο  . Η μεσοκάθετος του ευθύγραμμου τμήματος
. Η μεσοκάθετος του ευθύγραμμου τμήματος  τέμνει τις ευθείες
τέμνει τις ευθείες  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Να αποδείξετε, ότι τα σημεία
αντίστοιχα. Να αποδείξετε, ότι τα σημεία  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά. 4. Τον φυσικό αριθμό
 τον ονομάζουμε «επιτυχημένο», αν για κάθε φυσικό
τον ονομάζουμε «επιτυχημένο», αν για κάθε φυσικό  τέτοιο ώστε, αν ο
τέτοιο ώστε, αν ο 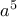 διαιρείτε με τον
διαιρείτε με τον  τότε και ο
τότε και ο  διαιρείτε με τον
διαιρείτε με τον  . Να βρείτε το πλήθος των επιτυχημένων φυσικών αριθμών μικρότερων του 2010.
. Να βρείτε το πλήθος των επιτυχημένων φυσικών αριθμών μικρότερων του 2010.Δεύτερη μέρα
5. Οι μη μηδενικοί αριθμοί
 είναι τέτοιοι ώστε
είναι τέτοιοι ώστε  για κάθε
για κάθε  . Να αποδείξετε ότι
. Να αποδείξετε ότι  για κάθε
για κάθε  .
.6. Ευθείες, εφαπτόμενες κύκλου
 στα σημεία
στα σημεία  και
και  , τέμνονται στο σημείο
, τέμνονται στο σημείο  . Ευθεία διερχόμενη από το
. Ευθεία διερχόμενη από το  τέμνει τον κύκλο στα σημεία
τέμνει τον κύκλο στα σημεία  και
και  . Από τυχόν σημείο της χορδής
. Από τυχόν σημείο της χορδής  φέρουμε ευθεία παράλληλη προς την
φέρουμε ευθεία παράλληλη προς την  . Να αποδείξετε ότι αυτή χωρίζει το μήκος των τεθλασμένων
. Να αποδείξετε ότι αυτή χωρίζει το μήκος των τεθλασμένων  και
και  σε ίσους λόγους.
σε ίσους λόγους.7. Υπάρχουν άραγε τρεις διαφορετικοί μη μηδενικοί ακέραιοι αριθμοί, το άθροισμα των οποίων ισούται με μηδέν και το άθροισμα των δέκατο τρίτων δυνάμεών τους να είναι τετράγωνο κάποιου φυσικού αριθμού;
8. Ονομάζουμε σκάλα ύψους
 το σχήμα που προκύπτει από τα κελιά ενός τετραγωνικού πλέγματος
το σχήμα που προκύπτει από τα κελιά ενός τετραγωνικού πλέγματος  που δε βρίσκονται πάνω από την διαγώνιο (στο σχήμα απεικονίζεται σκάλα ύψους 4). Με πόσους διαφορετικούς τρόπους μπορούμε να διαμερίσουμε σκάλα ύψους
που δε βρίσκονται πάνω από την διαγώνιο (στο σχήμα απεικονίζεται σκάλα ύψους 4). Με πόσους διαφορετικούς τρόπους μπορούμε να διαμερίσουμε σκάλα ύψους  σε ορθογώνια διαφορετικού μεταξύ τους εμβαδού, οι πλευρές των οποίων βρίσκονται πάνω στις ευθείες του πλέγματος;
σε ορθογώνια διαφορετικού μεταξύ τους εμβαδού, οι πλευρές των οποίων βρίσκονται πάνω στις ευθείες του πλέγματος;
 προσπεράσεις και επειδή οι σκιέρ κινούνται με σταθερή ταχύτητα, τότε σίγουρα τον πρώτο σκιέρ θα τον περάσουν
προσπεράσεις και επειδή οι σκιέρ κινούνται με σταθερή ταχύτητα, τότε σίγουρα τον πρώτο σκιέρ θα τον περάσουν  , για κάθε
, για κάθε  , άρα:
, άρα:  και
και  και αφού οι
και αφού οι  είναι μη μηδενικοί, θα είναι και
είναι μη μηδενικοί, θα είναι και 

 , για κάθε
, για κάθε  ος και ο
ος και ο  ος να τερμάτισαν ταυτόχρονα στην
ος να τερμάτισαν ταυτόχρονα στην  η θέση, γιατί να την αποκλείσουμε; (Δεν λέει στην εκφώνηση ότι τερμάτισαν με διαφορετική σειρά. Με τον ταυτόχρονο τερματισμό αυτών των δύο σκιέρ δεν έχουμε, νομίζω, προσπέραση και οι σταθερές ταχύτητες των
η θέση, γιατί να την αποκλείσουμε; (Δεν λέει στην εκφώνηση ότι τερμάτισαν με διαφορετική σειρά. Με τον ταυτόχρονο τερματισμό αυτών των δύο σκιέρ δεν έχουμε, νομίζω, προσπέραση και οι σταθερές ταχύτητες των  υπάρχει τουλάχιστον ένας ο οποίος και προσπέρασε τον 1 αλλά και προσπεράστηκε από τον 9. Αυτό είναι άτοπο αφού πρέπει και να τερμάτισε ψηλότερα από την πέμπτη θέση, αλλά και χαμηλότερα από την πέμπτη θέση.
υπάρχει τουλάχιστον ένας ο οποίος και προσπέρασε τον 1 αλλά και προσπεράστηκε από τον 9. Αυτό είναι άτοπο αφού πρέπει και να τερμάτισε ψηλότερα από την πέμπτη θέση, αλλά και χαμηλότερα από την πέμπτη θέση.
 μη μηδενικές τιμές
μη μηδενικές τιμές  διαφορετικές.
διαφορετικές. και την βρίσκω ίση με τον αριθμό
και την βρίσκω ίση με τον αριθμό  συνεπώς
συνεπώς άρα
άρα 
 αφού τότε
αφού τότε
 τέλειο τετράγωνο!
τέλειο τετράγωνο! , δείτε
, δείτε  ( λόγω μεσοκαθέτου )
( λόγω μεσοκαθέτου ) ( συμπληρωματικές της
( συμπληρωματικές της  ) , άρα ...
) , άρα ...
 και προκύπτει ότι ισχύει η ζητούμενη για κάθε
και προκύπτει ότι ισχύει η ζητούμενη για κάθε 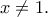
 δηλαδή ότι
δηλαδή ότι  Αυτό όμως προκύπτει από την αρχική, αφού
Αυτό όμως προκύπτει από την αρχική, αφού για κάθε
για κάθε 
 ως γινόμενο (διακεκριμένων) πρώτων παραγόντων. Τότε ο
ως γινόμενο (διακεκριμένων) πρώτων παραγόντων. Τότε ο  και για κάθε φυσικό
και για κάθε φυσικό  αν
αν  τότε
τότε  .
.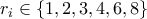 . [Είναι εύκολο να ελεγχθεί ότι αυτά τα
. [Είναι εύκολο να ελεγχθεί ότι αυτά τα  είναι δεκτά. Π.χ. αν
είναι δεκτά. Π.χ. αν  και
και  τότε
τότε 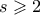 και άρα
και άρα  . Τα υπόλοιπα
. Τα υπόλοιπα  με
με  έχουμε αντιπαράδειγμα για
έχουμε αντιπαράδειγμα για  . Αν
. Αν  με
με  έχουμε αντιπαράδειγμα για
έχουμε αντιπαράδειγμα για  .]
.] . (Αφού
. (Αφού  .)
.) .
.  πολλαπλάσια του
πολλαπλάσια του  τα οποία είναι μικρότερα ή ίσα του
τα οποία είναι μικρότερα ή ίσα του  . Από αυτά τα
. Από αυτά τα  είναι πολλαπλάσια του
είναι πολλαπλάσια του  και
και  είναι πολλαπλάσια του
είναι πολλαπλάσια του 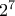 . Συνολικά λοιπόν υπάρχουν ακριβώς
. Συνολικά λοιπόν υπάρχουν ακριβώς 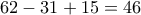 αριθμοί μικρότεροι ή ίσοι του
αριθμοί μικρότεροι ή ίσοι του  αριθμοί μικρότεροι ή ίσοι του
αριθμοί μικρότεροι ή ίσοι του  δεν διπλομετρήσαμε κάποιον αριθμό. Συνολικά λοιπόν έχουμε
δεν διπλομετρήσαμε κάποιον αριθμό. Συνολικά λοιπόν έχουμε  αποτυχημένους αριθμούς και άρα
αποτυχημένους αριθμούς και άρα  επιτυχημένοι αριθμοί.
επιτυχημένοι αριθμοί. που δεν είναι πολλαπλάσια του
που δεν είναι πολλαπλάσια του  . Έχουμε
. Έχουμε  . Έχουμε
. Έχουμε  .
. . Αφού τα εμβαδά είναι διαφορετικοί φυσικοί πρέπει
. Αφού τα εμβαδά είναι διαφορετικοί φυσικοί πρέπει  για κάθε
για κάθε  . Όμως το συνολικό εμβαδόν τον τετραγώνων ισούται με
. Όμως το συνολικό εμβαδόν τον τετραγώνων ισούται με  οπότε
οπότε  για κάθε
για κάθε  . Είναι τώρα απλό επαγωγικά να δούμε ότι υπάρχουν
. Είναι τώρα απλό επαγωγικά να δούμε ότι υπάρχουν  τρόποι να διαμερίσουμε την σκάλα.
τρόποι να διαμερίσουμε την σκάλα.