Al.Koutsouridis έγραψε: ↑Σάβ Απρ 16, 2016 3:14 pm
LXXIX Μαθηματική Ολυμπιάδα Μόσχας
Πρόβλημα 6. Στη χώρα των γλωσσολόγων υπάρχουν

γλώσσες. Στην οποία κατοικούν

άτομα, ο καθένας από τους οποίους γνωρίζει ακριβώς 3 γλώσσες και για διαφορετικά άτομα αυτή η τριάδα γλωσσών είναι διαφορετική. Είναι γνωστό ότι ο μέγιστος αριθμός ατόμων, οποιοιδήποτε δυο από τους οποίους μπορούν να συνομιλήσουν χωρίς μεταφραστή, ισούται με

. Προέκυψε ότι

. Να αποδείξετε ότι στη χώρα αυτή θα βρεθούν τουλάχιστον
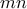
ζεύγη κατοίκων, οι οποίοι δε θα μπορέσουν να συνομιλήσουν χωρίς μεταφραστή.
Μεταφέρω την επίσημη λύση και το σχόλιο που συνοδεύει αυτό το πρόβλημα. Για την ιστόρία δυσκόλεψε πιρισσότερο από όλα τους συμμετέχοντες της 9ης τάξης, καθώς το έλυσαν 2 (+) σε σύνολο 890 μαθητών.
Λύση. Θα συμβολίσουμε με

το σύνολο

ατόμων, οι οποίοι μπορούν να συνομιλήσουν χωρίς μεταφραστές. Εξετάζουμε ένα τυχαία άτομο (τον κύριο

), που δεν εμπίπτει στο σύνολο

. Για αυτόν υπάρχει ένα τέτοιο άτομο του συνόλου

(ο κύριος

), ώστε η ένωση των γλωσσών τους να είναι κενό σύνολο. Θα εκτιμήσουμε το πλήθος εκείνων των ατόμων του συνόλου

, τα οποία μπορούν να συνομιλήσουν με τον κύριο

. Τέτοια άτομα έχουν τουλάχιστον μια κοινή γλώσσα και με τον κύριο

και με τον κύριο

(καθώς εμπίπτουν στο σύνολο

), άρα δεν είναι παραπάνω από

. Με αυτό το τρόπο, για κάθε άτομο, που δεν εμπίπτει στο σύνολο

, βρήκαμε τουλάχιστον

αντιπροσώπους του συνόλου

, οι οποίοι δεν μπορούν να συνομιλήσουν μαζί τους χωρίς μεταφραστή. Οπότε στο σύνολο τέτοια ζεύγη θα είναι

.
Σχόλιο. Το πρόβλημα σχετίζεται με ένα καθόλα γνωστό και σημαντικό τομέα της σύγχρονης θεωρίας γράφων. Και συγκεκριμένα, ένας γράφος ονομάζεται
γράφος Κνέσερ( Kneser), αν οι κορυφές του είναι όλα τα δυνατά υποσύνολα δύναμης

του συνόλου

και ακμές του, ζεύγη μη τεμνόμενων υποσυνόλων. Για τους γράφους Κνέσερ υπάρχει «δημοφιλής» (εκλαϊκευμένη) βιβλιογραφία: Βλ. [1], [2]. Στο πρόβλημα 6 έχουμε να κάνουμε με ένα γράφο Κνέσερ, στον οποίο

. Κάθε κορυφή του είναι μια τριάδα γλωσσών (ή αν θέλετε, γλωσσολόγος, που ξέρει αυτές τις τρεις γλώσσες). Δυο κορυφές ενώνονται με ακμή, αν οι αντίστοιχοι γλωσσολόγοι δεν μπορούν συνομιλήσουν χωρίς μεταφραστή. Θυμίζουμε, ότι ένα σύνολο κορυφών ενός γράφου ονομάζεται
ανεξάρτητο, αν οποιεσδήποτε δυο κορυφές σε αυτό δεν ενώνονται με ακμή. Η δύναμη του μεγαλύτερου ανεξάρτητου υποσυνόλου κορυφών ενός γράφου

ονομάζεται αριθμός ανεξαρτησίας και συμβολίζεται με

. Με αυτούς τους όρους το πρόβλημα 6 διατυπώνεται ως:
«έστω ότι δίνεται ένας υπογράφος  ενός γράφου Κνέσερ με
ενός γράφου Κνέσερ με  και
και  κορυφές, εξάλλου
κορυφές, εξάλλου  και
και 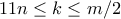 . Να αποδείξετε τότε, ότι ο αριθμός ακμών του γράφου
. Να αποδείξετε τότε, ότι ο αριθμός ακμών του γράφου  είναι τουλάχιστον
είναι τουλάχιστον 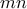 »
».
Το πρόβλημα σε τέτοια διατύπωση μη τετριμμένα χρησιμοποιεί ακριβώς την δομή ενός γράφου Κνέσερ. Το γεγονός είναι ότι υπάρχει το κλασικό
θεώρημα του Τουράν: αν γράφος με

κορυφές έχει βαθμό ανεξαρτησίας

, τότε έχει «περίπου»

ακμές ή περισσότερες. Στην περίπτωσή μας αυτή η εκτίμηση έχει το μέγεθος της τάξης του

, καθόλα διαφορετικό του
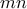
και αυτό είναι πολύ σημαντικό.
Να σημειώσουμε ότι ο αριθμός ανεξαρτησίας όλου του γράφου Κνέσερ είναι ίσος με

, αν
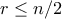
. Αυτό είναι το γνωστό
θεώρημα Έρντος-Κο-Ραντό, την απόδειξη του οποίου για παράδειγμα μπορείτε να διαβάσετε στο [3]. Το πρόβλημα 6 προέκυψε κατά την στιγμή, που ο θεματοδότης και οι μαθητές του μπόρεσαν να δείξουν ότι σε τυχαίο υπογράφο ενός γράφου Κνέσερ ο αριθμός ανεξαρτησίας, αντίθετα με την διαίσθηση, σχεδόν δεν αλλάζει (βλ. [4]). Τώρα από αυτό έχει προκύψει σημαντικό επιστημονικό έργο, που επιτρέπει με νέα ματιά να κοιτάξουμε σε κλασικά αποτελέσματα της συνδυαστικής ακροτάτων (
extremal combinatorics) βλ. [5].
Να σημειώσουμε επίσης ότι η εκτίμηση στο πρόβλημα 6 μακράν δεν είναι η βέλτιστη. Μπορεί να βελτιωθεί, αποδεικνύοντας το ακόλουθο αποτέλεσμα:
«Στις συνθήκες του προβλήματος 6 τα μέγιστα ανεξάρτητα σύνολα αναγκαστικά θα αποτελούνται από κορυφές, οι οποίες όλες θα περιέχουν το ίδιο κοινό στοιχείο του συνόλου  .»
.» Προσπαθήστε να το αποδείξετε! Σε ποιο γενική μορφή ονομάζεται
θεώρημα Χίλτον-Μίλνερ (βλ. [3]).
[1] А. М. Райгородский. Гипотеза Кнезера и топологические методы в комбинаторике // «Квант», №1 (2011), 7—16. (Υπόθεση Κνέσερ και τοπολογικές μέθοδου στην συνδυαστική, κβαντ ν1, 2011)
[2] А. М. Райгородский. Гипотеза Кнезера и топологический метод в комбинаторике. М: МЦНМО, 2011.(Υπόθεση Κνέσερ και τοπολογικές μέθοδου στην συνδυαστική)
[3] А. М. Райгородский. Вероятность и алгебра в комбинаторике. М: МЦНМО, 2015. (Πιθανότητες και άλγεβρα στην συνδυαστική)
[4] Л. И. Боголюбский, А. С. Гусев, М. М. Пядёркин, А. М. Райгородский. Числа независимости и хроматические числа случайных подграфов некоторых дистанционных графов. Математический сборник, 206 (2015), №10, 3—36. (αριθμοί ανεξαρτησίας και χρωματικοί αριθμοί τυχαίων υπογράφων μερικών γράφων αποστάσεων)
[5] B. Bollobas, B. P. Narayanan, A. M. Raigorodskii. On the stability of the Erdos—Ko—Rado theorem // J. Comb. Th. Ser. A, 137 (2016), 64—78
Υγ. Διάφοροι σύνδεσμοι στο κείμενο τοποθετήθηκαν από μένα.
Πηγή και στην προέκταση της διαμέσου
και στην προέκταση της διαμέσου 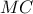 , προς το
, προς το  , θεωρούμε σημείο
, θεωρούμε σημείο  τέτοιο, ώστε
τέτοιο, ώστε 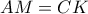 . Αν η γωνία
. Αν η γωνία  είναι ίση με
είναι ίση με  να δείξετε, ότι
να δείξετε, ότι  .
. , όπου
, όπου 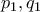 ακέραιοι αριθμοί. Βρίσκοντας τις ρίζες της
ακέραιοι αριθμοί. Βρίσκοντας τις ρίζες της  έγραψε μια νέα εξίσωση, την
έγραψε μια νέα εξίσωση, την  . Επανέλαβε αυτήν την διαδικασία άλλες τρεις φορές. Παρατήρησε ότι έλυσε τέσσερεις δευτεροβάθμιες εξισώσεις και καθεμιά τους είχε δυο διαφορετικές ακέραιες ρίζες (αν από τις δυο δυνατές εξισώσεις δυο διαφορετικές ρίζες έχει ακριβώς η μία, τότε πάντα διαλέγει αυτή, αν και οι δύο τότε οποιαδήποτε). Παρόλο που προσπάθησε πολύ ( ο Βασίλης είναι άριστος μαθητής), δεν μπόρεσε να γράψει πέμπτη εξίσωση, έτσι ώστε να έχει δυο διαφορετικές πραγματικές ρίζες. Ποια η εξίσωση που δόθηκε στον Βασίλη ως άσκηση;
. Επανέλαβε αυτήν την διαδικασία άλλες τρεις φορές. Παρατήρησε ότι έλυσε τέσσερεις δευτεροβάθμιες εξισώσεις και καθεμιά τους είχε δυο διαφορετικές ακέραιες ρίζες (αν από τις δυο δυνατές εξισώσεις δυο διαφορετικές ρίζες έχει ακριβώς η μία, τότε πάντα διαλέγει αυτή, αν και οι δύο τότε οποιαδήποτε). Παρόλο που προσπάθησε πολύ ( ο Βασίλης είναι άριστος μαθητής), δεν μπόρεσε να γράψει πέμπτη εξίσωση, έτσι ώστε να έχει δυο διαφορετικές πραγματικές ρίζες. Ποια η εξίσωση που δόθηκε στον Βασίλη ως άσκηση; και το κέντρο
και το κέντρο  του περιγεγραμμένου κύκλου του. Ευθεία κάθετη στην πλευρά
του περιγεγραμμένου κύκλου του. Ευθεία κάθετη στην πλευρά  , τέμνει την πλευρά
, τέμνει την πλευρά  και την ευθεία
και την ευθεία  στα σημεία
στα σημεία  και
και  αντίστοιχα. Να αποδείξετε ότι τα σημεία
αντίστοιχα. Να αποδείξετε ότι τα σημεία 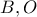 και τα μέσα των τμημάτων
και τα μέσα των τμημάτων  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά. γλώσσες. Στην οποία κατοικούν
γλώσσες. Στην οποία κατοικούν  άτομα, ο καθένας από τους οποίους γνωρίζει ακριβώς 3 γλώσσες και για διαφορετικά άτομα αυτή η τριάδα γλωσσών είναι διαφορετική. Είναι γνωστό ότι ο μέγιστος αριθμός ατόμων, οποιοιδήποτε δυο από τους οποίους μπορούν να συνομιλήσουν χωρίς μεταφραστή, ισούται με
άτομα, ο καθένας από τους οποίους γνωρίζει ακριβώς 3 γλώσσες και για διαφορετικά άτομα αυτή η τριάδα γλωσσών είναι διαφορετική. Είναι γνωστό ότι ο μέγιστος αριθμός ατόμων, οποιοιδήποτε δυο από τους οποίους μπορούν να συνομιλήσουν χωρίς μεταφραστή, ισούται με  . Προέκυψε ότι
. Προέκυψε ότι  . Να αποδείξετε ότι στη χώρα αυτή θα βρεθούν τουλάχιστον
. Να αποδείξετε ότι στη χώρα αυτή θα βρεθούν τουλάχιστον 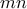 ζεύγη κατοίκων, οι οποίοι δε θα μπορέσουν να συνομιλήσουν χωρίς μεταφραστή.
ζεύγη κατοίκων, οι οποίοι δε θα μπορέσουν να συνομιλήσουν χωρίς μεταφραστή.
 φέρνω παράλληλη στην
φέρνω παράλληλη στην  που τέμνει την από το
που τέμνει την από το  κάθετη στην
κάθετη στην  .
.  και ότι
και ότι 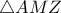 ισόπλευρο
ισόπλευρο  και επειδή
και επειδή  παραλληλόγραμμο
παραλληλόγραμμο 
 και
και  :
:  που είναι το ζητούμενο.
που είναι το ζητούμενο. , ώστε
, ώστε  , οπότε το τρίγωνο
, οπότε το τρίγωνο  είναι ισόπλευρο. Τα τρίγωνα
είναι ισόπλευρο. Τα τρίγωνα  είναι ίσα
είναι ίσα  και
και  . Άρα
. Άρα 
 -ψήφιο αριθμό αντιστοιχούμε το διάνυσμα
-ψήφιο αριθμό αντιστοιχούμε το διάνυσμα  όπου ο
όπου ο  ισούται με το πλήθος των ψηφίων του αριθμού που ισούνται με
ισούται με το πλήθος των ψηφίων του αριθμού που ισούνται με  .
.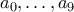 είναι μη αρνητικοί ακέραιοι με
είναι μη αρνητικοί ακέραιοι με 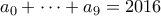 , υπάρχουν
, υπάρχουν 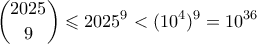

 τέλεια τετράγωνα στα οποία αντιστοιχεί το ίδιο διάνυσμα. Όλα αυτά τα τέλεια τετράγωνα είναι ασφαλώς περισσότερα από
τέλεια τετράγωνα στα οποία αντιστοιχεί το ίδιο διάνυσμα. Όλα αυτά τα τέλεια τετράγωνα είναι ασφαλώς περισσότερα από  ......(1) και
......(1) και  ......(2).
......(2).  και από την (1) έχουμε
και από την (1) έχουμε  και συνεπώς
και συνεπώς  άτοπο
άτοπο ......(3) και
......(3) και  .
.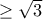 δεν βελτιώνεται σε
δεν βελτιώνεται σε  όπως βλέπουμε από το παράδειγμα
όπως βλέπουμε από το παράδειγμα 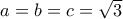 )
) Σίγουρα υπάρχει μία γωνία μεγαλύτερη ή ίση από
Σίγουρα υπάρχει μία γωνία μεγαλύτερη ή ίση από  και επειδή το τρίγωνο είναι οξυγώνιο, η δεύτερη μεγαλύτερη είναι σίγουρα τουλάχιστον
και επειδή το τρίγωνο είναι οξυγώνιο, η δεύτερη μεγαλύτερη είναι σίγουρα τουλάχιστον 
![xyz = x+y+z \geqslant 3\sqrt[3]{xyz} xyz = x+y+z \geqslant 3\sqrt[3]{xyz}](/forum/ext/geomar/texintegr/latexrender/pictures/d1fffbc2ba11ff14bd905fa7509caf5a.png) . Οπότε παίρνουμε
. Οπότε παίρνουμε  . Άρα κάποιο από τα
. Άρα κάποιο από τα  είναι μεγαλύτερο ή ίσο του
είναι μεγαλύτερο ή ίσο του  αφού σε αντίθετη περίπτωση θα είχαμε
αφού σε αντίθετη περίπτωση θα είχαμε  .
.  , έστω τους
, έστω τους  και
και  , τότε είναι
, τότε είναι  , άτοπο.
, άτοπο. οι δύο μεγαλύτεροι, τότε για τον τρίτο είναι υποχρεωτικά
οι δύο μεγαλύτεροι, τότε για τον τρίτο είναι υποχρεωτικά  .
.  τότε
τότε  , οπότε
, οπότε  , άτοπο.
, άτοπο. και
και  τα μέσα των τμημάτων
τα μέσα των τμημάτων  και
και  αντίστοιχα. Ζητείται να αποδειχθεί ότι το τετράπλευρο
αντίστοιχα. Ζητείται να αποδειχθεί ότι το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο.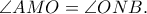
 και
και  τα μέσα των τμημάτων
τα μέσα των τμημάτων  και
και  αντίστοιχα. Αρκεί να αποδείξουμε ότι τα (ορθογώνια) τρίγωνα
αντίστοιχα. Αρκεί να αποδείξουμε ότι τα (ορθογώνια) τρίγωνα  και
και 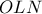 είναι όμοια. Εμομένως, αρκεί να αποδείξουμε ότι
είναι όμοια. Εμομένως, αρκεί να αποδείξουμε ότι 



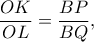 δηλαδή αρκεί να δείξουμε ότι τα τρίγωνα
δηλαδή αρκεί να δείξουμε ότι τα τρίγωνα  και
και  είναι όμοια. Αυτό, όμως, προκύπτει από τις ισότητες γωνιών
είναι όμοια. Αυτό, όμως, προκύπτει από τις ισότητες γωνιών



 οι (διαφορετικές μεταξύ τους) ακέραιες ρίζες της τέταρτης εξίσωσης.
οι (διαφορετικές μεταξύ τους) ακέραιες ρίζες της τέταρτης εξίσωσης.

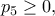


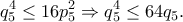
 τότε
τότε  πράγμα άτοπο. Επομένως, είναι
πράγμα άτοπο. Επομένως, είναι  και
και  οπότε
οπότε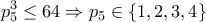

 που ικανοποιούν τις σχέσεις
που ικανοποιούν τις σχέσεις  είναι τα
είναι τα  και
και 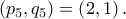
 η τρίτη είναι η
η τρίτη είναι η  η δεύτερη είναι η
η δεύτερη είναι η  και η πρώτη είναι η
και η πρώτη είναι η  .
. ), που δεν εμπίπτει στο σύνολο
), που δεν εμπίπτει στο σύνολο  ), ώστε η ένωση των γλωσσών τους να είναι κενό σύνολο. Θα εκτιμήσουμε το πλήθος εκείνων των ατόμων του συνόλου
), ώστε η ένωση των γλωσσών τους να είναι κενό σύνολο. Θα εκτιμήσουμε το πλήθος εκείνων των ατόμων του συνόλου  (καθώς εμπίπτουν στο σύνολο
(καθώς εμπίπτουν στο σύνολο  . Με αυτό το τρόπο, για κάθε άτομο, που δεν εμπίπτει στο σύνολο
. Με αυτό το τρόπο, για κάθε άτομο, που δεν εμπίπτει στο σύνολο  αντιπροσώπους του συνόλου
αντιπροσώπους του συνόλου  .
. του συνόλου
του συνόλου  και ακμές του, ζεύγη μη τεμνόμενων υποσυνόλων. Για τους γράφους Κνέσερ υπάρχει «δημοφιλής» (εκλαϊκευμένη) βιβλιογραφία: Βλ. [1], [2]. Στο πρόβλημα 6 έχουμε να κάνουμε με ένα γράφο Κνέσερ, στον οποίο
και ακμές του, ζεύγη μη τεμνόμενων υποσυνόλων. Για τους γράφους Κνέσερ υπάρχει «δημοφιλής» (εκλαϊκευμένη) βιβλιογραφία: Βλ. [1], [2]. Στο πρόβλημα 6 έχουμε να κάνουμε με ένα γράφο Κνέσερ, στον οποίο  . Κάθε κορυφή του είναι μια τριάδα γλωσσών (ή αν θέλετε, γλωσσολόγος, που ξέρει αυτές τις τρεις γλώσσες). Δυο κορυφές ενώνονται με ακμή, αν οι αντίστοιχοι γλωσσολόγοι δεν μπορούν συνομιλήσουν χωρίς μεταφραστή. Θυμίζουμε, ότι ένα σύνολο κορυφών ενός γράφου ονομάζεται
. Κάθε κορυφή του είναι μια τριάδα γλωσσών (ή αν θέλετε, γλωσσολόγος, που ξέρει αυτές τις τρεις γλώσσες). Δυο κορυφές ενώνονται με ακμή, αν οι αντίστοιχοι γλωσσολόγοι δεν μπορούν συνομιλήσουν χωρίς μεταφραστή. Θυμίζουμε, ότι ένα σύνολο κορυφών ενός γράφου ονομάζεται  ονομάζεται αριθμός ανεξαρτησίας και συμβολίζεται με
ονομάζεται αριθμός ανεξαρτησίας και συμβολίζεται με  . Με αυτούς τους όρους το πρόβλημα 6 διατυπώνεται ως: «έστω ότι δίνεται ένας υπογράφος
. Με αυτούς τους όρους το πρόβλημα 6 διατυπώνεται ως: «έστω ότι δίνεται ένας υπογράφος  και
και 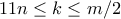 . Να αποδείξετε τότε, ότι ο αριθμός ακμών του γράφου
. Να αποδείξετε τότε, ότι ο αριθμός ακμών του γράφου  ακμές ή περισσότερες. Στην περίπτωσή μας αυτή η εκτίμηση έχει το μέγεθος της τάξης του
ακμές ή περισσότερες. Στην περίπτωσή μας αυτή η εκτίμηση έχει το μέγεθος της τάξης του  , αν
, αν 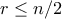 . Αυτό είναι το γνωστό
. Αυτό είναι το γνωστό  .» Προσπαθήστε να το αποδείξετε! Σε ποιο γενική μορφή ονομάζεται
.» Προσπαθήστε να το αποδείξετε! Σε ποιο γενική μορφή ονομάζεται