Έστω
 πραγματικοί αριθμοί που ικανοποιούν
πραγματικοί αριθμοί που ικανοποιούν 
 ,
,  και
και  . Να βρεθεί η μέγιστη τιμή του γινομένου
. Να βρεθεί η μέγιστη τιμή του γινομένου  .
.Α2 (Αλβανία)
Αν
 τότε να βρείτε την τιμή της παράστασης
τότε να βρείτε την τιμή της παράστασης  .
.A3 (Mαυροβούνιο)
Έστω
 θετικοί πραγματικοί αριθμοί. Να δείξετε ότι
θετικοί πραγματικοί αριθμοί. Να δείξετε ότι ![\displaystyle\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt[3]{\frac{c}{a}}>2. \displaystyle\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt[3]{\frac{c}{a}}>2.](/forum/ext/geomar/texintegr/latexrender/pictures/67d3ed5017d3158aae9111a8aa4ed2e9.png)
Α4 (Ελλάδα, Σ.Μ.)
Οι θετικοί πραγματικοί
 είναι τέτοιοι ώστε
είναι τέτοιοι ώστε  . Να βρείτε την ελάχιστη τιμή της παράστασης
. Να βρείτε την ελάχιστη τιμή της παράστασης .
. A5 (FYROM)
Οι θετικοί πραγματικοί
 είναι τέτοιοι ώστε
είναι τέτοιοι ώστε  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.Το πρόβλημα Α4 τέθηκε στον διαγωνισμό σαν πρόβλημα 2.
Το πρόβλημα Α2 αποκλείστηκε από τη λίστα.

 και τότε είναι προφανές ότι
και τότε είναι προφανές ότι  . Η ανισότητα είναι ισοδύναμη με
. Η ανισότητα είναι ισοδύναμη με  που είναι ισοδύναμη με
που είναι ισοδύναμη με  . Όμως από την ανισότητα C-S παίρνουμε ότι
. Όμως από την ανισότητα C-S παίρνουμε ότι  όπου χρησιμοποιήθηκε η (1) στο τελευταίο βήμα.
όπου χρησιμοποιήθηκε η (1) στο τελευταίο βήμα.![\displaystyle{\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt[3]{\frac{c}{a}}=\frac{a}{b}+\frac{1}{2}\sqrt{\frac{b}{c}}+\frac{1}{2}\sqrt{\frac{b}{c}}+\frac{1}{3}\sqrt[3]{\frac{c}{a}}+\frac{1}{3}\sqrt[3]{\frac{c}{a}}+\frac{1}{3}\sqrt[3]{\frac{c}{a}}\geq} \displaystyle{\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt[3]{\frac{c}{a}}=\frac{a}{b}+\frac{1}{2}\sqrt{\frac{b}{c}}+\frac{1}{2}\sqrt{\frac{b}{c}}+\frac{1}{3}\sqrt[3]{\frac{c}{a}}+\frac{1}{3}\sqrt[3]{\frac{c}{a}}+\frac{1}{3}\sqrt[3]{\frac{c}{a}}\geq}](/forum/ext/geomar/texintegr/latexrender/pictures/84e448ac42fb92e200f3f98c5588ca80.png)
![\displaystyle{\geq 6\sqrt[6]{\frac{a}{b}\frac{b}{4c}\frac{c}{27a}}=\frac{6}{\sqrt[6]{4\cdot 27}}.} \displaystyle{\geq 6\sqrt[6]{\frac{a}{b}\frac{b}{4c}\frac{c}{27a}}=\frac{6}{\sqrt[6]{4\cdot 27}}.}](/forum/ext/geomar/texintegr/latexrender/pictures/e3973453a1812970ab4d08076411710d.png)
![\displaystyle{3>\sqrt[6]{4\cdot 27}} \displaystyle{3>\sqrt[6]{4\cdot 27}}](/forum/ext/geomar/texintegr/latexrender/pictures/6d891cba73e9ca46ddfe2e0cf99330f0.png) δηλαδή
δηλαδή  η οποία ισχύει.
η οποία ισχύει. ...
... Αν
Αν  , να αποδειχθεί ότι:
, να αποδειχθεί ότι: ![\displaystyle{\dfrac{x}{y}+\sqrt{\dfrac{y}{z}}+\sqrt[3]{\dfrac{z}{x}}>\dfrac{3}{2}} \displaystyle{\dfrac{x}{y}+\sqrt{\dfrac{y}{z}}+\sqrt[3]{\dfrac{z}{x}}>\dfrac{3}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/5783a6930df7ab9bf3ecf9321d6146cf.png)
 .
.  γράφεται
γράφεται 
 και επιτυγχάνεται για
και επιτυγχάνεται για  .
. . Τότε είναι
. Τότε είναι  και η ισότητα ισχύει όταν
και η ισότητα ισχύει όταν 
 διαδοχικούς ακεραίους. Ποιο είναι το μέγιστο δυνατό (σε πληθάριθμο) υποσύνολό του ώστε να μην υπάρχουν δύο στοιχεία του υποσυνόλου που το άθροισμά τους να διαιρείται από τη διαφορά τους.
διαδοχικούς ακεραίους. Ποιο είναι το μέγιστο δυνατό (σε πληθάριθμο) υποσύνολό του ώστε να μην υπάρχουν δύο στοιχεία του υποσυνόλου που το άθροισμά τους να διαιρείται από τη διαφορά τους. διαιρείται με το
διαιρείται με το  αν και μόνο αν το
αν και μόνο αν το  διαιρείται με το
διαιρείται με το  τέτοιος ώστε ο
τέτοιος ώστε ο  αν και μόνο αν ο
αν και μόνο αν ο  θετικοί ακέραιοι. Να αποδείξετε ότι το γινόμενο όλων των διαφορών από τα όλα τα πιθανά ζεύγη, διαιρείται από το
θετικοί ακέραιοι. Να αποδείξετε ότι το γινόμενο όλων των διαφορών από τα όλα τα πιθανά ζεύγη, διαιρείται από το 

 και πρώτος αριθμός
και πρώτος αριθμός  ώστε
ώστε  .
.  καταλήγουμε στην
καταλήγουμε στην 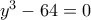 που δίνει
που δίνει  και άρα
και άρα  .
. αλλά παρατηρούμε ότι
αλλά παρατηρούμε ότι  και
και  οπότε
οπότε  .
.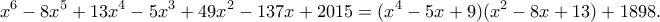

 θετικός ακέραιος, κάτι που εσύ πρότεινες να μπει για να λιγοστέψουν οι περιπτώσεις.
θετικός ακέραιος, κάτι που εσύ πρότεινες να μπει για να λιγοστέψουν οι περιπτώσεις. τον αριθμό
τον αριθμό  .
. .
.  , τότε
, τότε 
 , πολ.
, πολ. τότε
τότε  όπου ο αριθμός
όπου ο αριθμός  έχει
έχει  άσσους άρα από το α) γράφεται
άσσους άρα από το α) γράφεται  ( όπου
( όπου 
 δεν διαιρείται με το
δεν διαιρείται με το  δεν διαιρείται με το
δεν διαιρείται με το  τότε
τότε  που ούτε αυτός διαιρείται με το
που ούτε αυτός διαιρείται με το  δεν διαιρείται με το
δεν διαιρείται με το  διαιρείται από τον
διαιρείται από τον  και ο αριθμός
και ο αριθμός  γράφεται:
γράφεται:  , άρα πολλαπλάσιο του
, άρα πολλαπλάσιο του  που διαιρείται με το
που διαιρείται με το 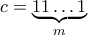 διαιρείται από to
διαιρείται από to  . τότε, και ο αριθμός
. τότε, και ο αριθμός  θα διαιρείται με το 41, άτοπο, γιατί ο αριθμός που προκύπτει έχει λιγότερες μονάδες από
θα διαιρείται με το 41, άτοπο, γιατί ο αριθμός που προκύπτει έχει λιγότερες μονάδες από  !!!.
!!!. , π.χ.
, π.χ.  και
και  ;
; όχι απαραίτητα για το
όχι απαραίτητα για το  με
με  . Αυτό θα απαντήσει ουσιαστικά και στο ερώτημα του Κυπριανού-Ιάσονα. (Ποιο απ' τα δύο ονόματα προτιμάς να χρησιμοποιούμε; Η μήπως και τα δύο μαζί;)
. Αυτό θα απαντήσει ουσιαστικά και στο ερώτημα του Κυπριανού-Ιάσονα. (Ποιο απ' τα δύο ονόματα προτιμάς να χρησιμοποιούμε; Η μήπως και τα δύο μαζί;) . Προφανώς,
. Προφανώς,  .
.![4p^2=(a-b)(a^2-ab+b^2)=(a-b)((a-b)^2+ab)>(a-b)^3 \Rightarrow a-b <\sqrt[3]{4p^2} 4p^2=(a-b)(a^2-ab+b^2)=(a-b)((a-b)^2+ab)>(a-b)^3 \Rightarrow a-b <\sqrt[3]{4p^2}](/forum/ext/geomar/texintegr/latexrender/pictures/155801efbc24be6aed4a2f6b7633817c.png) (1).
(1). ή
ή  .
. . Τότε,
. Τότε,  και από (1)
και από (1) ![a-b<\sqrt[3]{16} \Rightarrow a-b<2 \Rightarrow a-b=1 a-b<\sqrt[3]{16} \Rightarrow a-b<2 \Rightarrow a-b=1](/forum/ext/geomar/texintegr/latexrender/pictures/cb83a4c615bd07c9926119b6140ed819.png) , αφού
, αφού  και
και  . Λύνοντας το σύστημα δεν προκύπτει λύση.
. Λύνοντας το σύστημα δεν προκύπτει λύση. . Εφαρμόζοντας την παραπάνω διαδικασία, δεν προκύπτει πάλι λύση.
. Εφαρμόζοντας την παραπάνω διαδικασία, δεν προκύπτει πάλι λύση.![a-b<\sqrt[3]{4p^2} \leqslant p \Rightarrow a-b<p a-b<\sqrt[3]{4p^2} \leqslant p \Rightarrow a-b<p](/forum/ext/geomar/texintegr/latexrender/pictures/a5c8348da5d705ae34c7bba97bbbfa6d.png) και αφού
και αφού  , έπεται ότι
, έπεται ότι  ή
ή  .
. , άρα
, άρα  , καθώς
, καθώς  άρτιος, ως γινόμενο διαδοχικών φυσικών.
άρτιος, ως γινόμενο διαδοχικών φυσικών. είναι άρτιος.
είναι άρτιος. , άρα
, άρα 
 , άτοπο, γιατί τα τετραγωνικά υπόλοιπα
, άτοπο, γιατί τα τετραγωνικά υπόλοιπα  είναι
είναι  .
. και
και  .
. (αν
(αν  , τότε
, τότε  , άτοπο).
, άτοπο). ή
ή  .
. , άτοπο, καθώς το
, άτοπο, καθώς το  .
.