G.1
Έστω
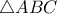 οξυγώνιο τρίγωνο με ορθόκεντρο
οξυγώνιο τρίγωνο με ορθόκεντρο 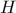 .Θεωρούμε σημείο
.Θεωρούμε σημείο 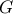 έτσι ώστε το τετράπλευρο
έτσι ώστε το τετράπλευρο 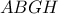 να είναι παραλληλόγραμμο και σημείο
να είναι παραλληλόγραμμο και σημείο  της ευθείας
της ευθείας 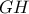 έτσι ώστε η
έτσι ώστε η  να διχοτομεί την
να διχοτομεί την 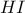 .Ο περιγεγραμμένος κύκλος του τριγώνου
.Ο περιγεγραμμένος κύκλος του τριγώνου 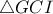 τέμνει την
τέμνει την  στο
στο 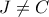 .Να δειχθεί ότι
.Να δειχθεί ότι 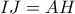 .
.G.2
Έστω τρίγωνο
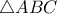 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  με κέντρο
με κέντρο  .Κύκλος
.Κύκλος  με κέντρο
με κέντρο  τέμνει την
τέμνει την  στα
στα 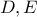 ώστε το
ώστε το  να βρίσκεται μεταξύ των
να βρίσκεται μεταξύ των 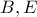 .Έστω
.Έστω  τα κοινά σημεία των
τα κοινά σημεία των 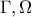 .Έστω ότι το
.Έστω ότι το  ανήκει στο τόξο
ανήκει στο τόξο 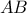 του
του  που δεν περιέχει το
που δεν περιέχει το  και το
και το 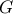 ανήκει στο τόξο
ανήκει στο τόξο  του
του  που δεν περιέχει το
που δεν περιέχει το  .Οι περιγεγραμμένοι κύκλοι των τριγώνων
.Οι περιγεγραμμένοι κύκλοι των τριγώνων 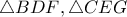 τέμνουν τις πλευρές
τέμνουν τις πλευρές  στα
στα 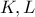 αντίστοιχα.Οι ευθείες
αντίστοιχα.Οι ευθείες 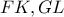 τέμνονται στο
τέμνονται στο  .Να δειχθεί ότι τα σημεία
.Να δειχθεί ότι τα σημεία 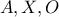 είναι συνευθειακά.
είναι συνευθειακά.G.3
Έστω τρίγωνο
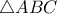 τέτοιο ώστε
τέτοιο ώστε 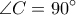 και έστω
και έστω 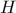 το ίχνος του ύψους από το
το ίχνος του ύψους από το  .Σημείο
.Σημείο  επιλέγεται στο εσωτερικό του τριγώνου
επιλέγεται στο εσωτερικό του τριγώνου 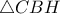 έτσι ώστε η
έτσι ώστε η  να διχοτομεί την
να διχοτομεί την  .Έστω
.Έστω  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 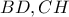 και
και  το ημικύκλιο διαμέτρου
το ημικύκλιο διαμέτρου 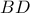 το οποίο τέμνει το τμήμα
το οποίο τέμνει το τμήμα  σε εσωτερικό σημείο.Ευθεία διερχομένη από το
σε εσωτερικό σημείο.Ευθεία διερχομένη από το  εφάπτεται του
εφάπτεται του  στο
στο  .Να δειχθεί ότι οι ευθείες
.Να δειχθεί ότι οι ευθείες 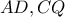 τέμνονται επί του
τέμνονται επί του  .
.G.4
Έστω οξυγώνιο τρίγωνο
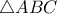 και
και  το μέσο του τμήματος
το μέσο του τμήματος  .Κύκλος
.Κύκλος  διερχόμενος από τα
διερχόμενος από τα 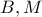 τέμνει ξανά τις
τέμνει ξανά τις 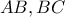 στα
στα  αντίστοιχα.Θεωρούμε σημείο
αντίστοιχα.Θεωρούμε σημείο  τέτοιο ώστε το τετράπλευρο
τέτοιο ώστε το τετράπλευρο 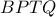 να είναι παραλληλόγραμμο.Αν το
να είναι παραλληλόγραμμο.Αν το  ανήκει στον περιγεγραμμένο κύκλο του
ανήκει στον περιγεγραμμένο κύκλο του 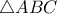 ,να βρεθούν όλες οι δυνατές τιμές του λόγου
,να βρεθούν όλες οι δυνατές τιμές του λόγου 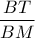 .
.G.5
Έστω τρίγωνο
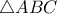 με
με 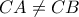 κι έστω
κι έστω 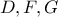 τα μέσα των τμημάτων
τα μέσα των τμημάτων 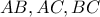 αντίστοιχα.Κύκλος
αντίστοιχα.Κύκλος  που διέρχεται από το
που διέρχεται από το  κι εφάπτεται της
κι εφάπτεται της  στο
στο  ,τέμνει τα τμήματα
,τέμνει τα τμήματα 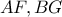 στα σημεία
στα σημεία 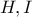 αντίστοιχα.Έστω
αντίστοιχα.Έστω 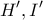 τα συμμετρικά των
τα συμμετρικά των 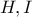 αντίστοιχα,ως προς τα
αντίστοιχα,ως προς τα  αντίστοιχα.Η ευθεία
αντίστοιχα.Η ευθεία 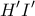 τέμνει τις
τέμνει τις 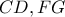 στα
στα 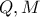 αντίστοιχα.Η ευθεία
αντίστοιχα.Η ευθεία 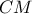 τέμνει ξανά τον
τέμνει ξανά τον  στο σημείο
στο σημείο  .Να δειχθεί ότι
.Να δειχθεί ότι 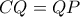 .
.G.6
Έστω
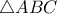 οξυγώνιο τρίγωνο με
οξυγώνιο τρίγωνο με 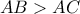 κι έστω
κι έστω  ο περιγεγραμμένος κύκλος του.Έστω
ο περιγεγραμμένος κύκλος του.Έστω 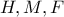 το ορθόκεντρο του
το ορθόκεντρο του 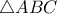 ,το μέσο του τμήματος
,το μέσο του τμήματος  και το ίχνος του ύψους από το
και το ίχνος του ύψους από το  αντίστοιχα.Έστω
αντίστοιχα.Έστω 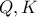 σημεία στον
σημεία στον  τέτοια ώστε
τέτοια ώστε 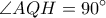 και
και 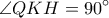 .Να δειχθεί ότι οι περιγεγραμμένοι κύκλοι των τριγώνων
.Να δειχθεί ότι οι περιγεγραμμένοι κύκλοι των τριγώνων 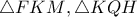 εφαπτονται μεταξύ τους.
εφαπτονται μεταξύ τους.G.7
Έστω
 κυρτό τετράπλευρο και
κυρτό τετράπλευρο και 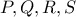 σημεία των τμημάτων
σημεία των τμημάτων 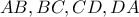 αντίστοιχα.Τα τμήματα
αντίστοιχα.Τα τμήματα 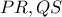 τέμνονται στο
τέμνονται στο  .Αν τα τετράπλευρα
.Αν τα τετράπλευρα 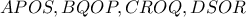 είναι όλα περιγράψιμα,να δειχθεί ότι οι ευθείες
είναι όλα περιγράψιμα,να δειχθεί ότι οι ευθείες 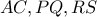 συντρέχουν.
συντρέχουν.G.8
Ονομάζουμε τριγωνοποίηση ενός κυρτού πολυγώνου
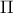 μια διαμέρισή του σε τρίγωνα,χρησιμοποιώντας διαγωνίους οι οποίες δεν έχουν κοινά σημεία πέραν των κορυφών του
μια διαμέρισή του σε τρίγωνα,χρησιμοποιώντας διαγωνίους οι οποίες δεν έχουν κοινά σημεία πέραν των κορυφών του 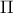 .Λέμε ότι μια τριγωνοποίηση είναι Ταϊλανδοποίηση αν όλα τα τρίγωνα που την αποτελούν έχουν το ίδιο εμβαδόν.Να αποδειχθεί ότι κάθε δύο Ταϊλανδοποιήσεις διαφέρουν σε ακριβώς δύο τρίγωνα (Με άλλα λόγια,να αποδειχθεί ότι,για κάθε δύο Ταϊλανδοποιήσεις,είναι δυνατόν να αντικαταστήσουμε ένα ζεύγος τριγώνων της μιας με ένα άλλο ζεύγος,και να καταλήξουμε στην άλλη).
.Λέμε ότι μια τριγωνοποίηση είναι Ταϊλανδοποίηση αν όλα τα τρίγωνα που την αποτελούν έχουν το ίδιο εμβαδόν.Να αποδειχθεί ότι κάθε δύο Ταϊλανδοποιήσεις διαφέρουν σε ακριβώς δύο τρίγωνα (Με άλλα λόγια,να αποδειχθεί ότι,για κάθε δύο Ταϊλανδοποιήσεις,είναι δυνατόν να αντικαταστήσουμε ένα ζεύγος τριγώνων της μιας με ένα άλλο ζεύγος,και να καταλήξουμε στην άλλη).
Τα προβλήματα G.2,G.6 είναι τα προβλήματα 4,3 της περσινής ολυμπιάδας.Μπορείτε να τα δείτε,μαζί με τις λύσεις τους,σε αυτό το θέμα.
Το G.1 χρησιμοποιήθηκε στο διαγωνισμό επιλογής των Σκοπίων (όπως και το Ν.3,το οποίο δημοσίευσε ο Σιλουανός εδώ),το G.3 στο διαγωνισμό επιλογής του Ιράν,και τα G.5,G.7 στο διαγωνισμό επιλογής της Ρουμανίας.

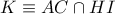 . Από το εγγράψιμο
. Από το εγγράψιμο 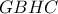 έχουμε
έχουμε 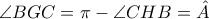 . Άρα
. Άρα 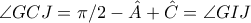 και αφού
και αφού 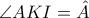 παίρνουμε
παίρνουμε 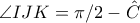 .
. 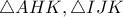 έχουν
έχουν 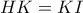 και
και 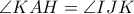 , οπότε
, οπότε 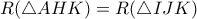 . Άρα οι πλευρές απέναντι από τις παραπληρωματικές
. Άρα οι πλευρές απέναντι από τις παραπληρωματικές 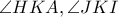 θα είναι ίσες και έτσι
θα είναι ίσες και έτσι 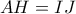 .
.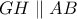 θα είναι
θα είναι 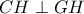 άρα το τετράπλευρο
άρα το τετράπλευρο 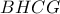 είναι εγγράψιμο οπότε με κυνήγι γωνιών έχουμε:
είναι εγγράψιμο οπότε με κυνήγι γωνιών έχουμε: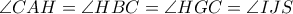 .
. του
του  ως προς το
ως προς το  .Επειδή οι διαγώνιοί του διχοτομούνται, το τετράπλευρο
.Επειδή οι διαγώνιοί του διχοτομούνται, το τετράπλευρο 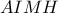 είναι παραλληλόγραμμο.Άρα
είναι παραλληλόγραμμο.Άρα 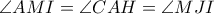 οπότε
οπότε 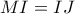
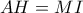 άρα
άρα 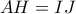 , το ζητούμενο.
, το ζητούμενο. ως διάκεντρος των κύκλων
ως διάκεντρος των κύκλων 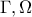 είναι μεσοκάθετος της κοινής χορδής τους
είναι μεσοκάθετος της κοινής χορδής τους  αρκεί να αποδείξουμε ότι το
αρκεί να αποδείξουμε ότι το  ανήκει στη μεσοκάθετο αυτή ή
ανήκει στη μεσοκάθετο αυτή ή 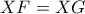 .
. οι τομές των
οι τομές των 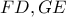 με τον κύκλο
με τον κύκλο  αντίστοιχα.Τότε χρησιμοποιώντας και το εγγεγραμμένο
αντίστοιχα.Τότε χρησιμοποιώντας και το εγγεγραμμένο 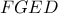 έχουμε ότι
έχουμε ότι 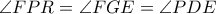 δηλαδή
δηλαδή 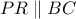
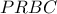 που είναι εγγεγραμμένο σε κύκλο είναι ισοσκελές, άρα
που είναι εγγεγραμμένο σε κύκλο είναι ισοσκελές, άρα 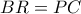 οπότε
οπότε 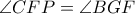 (εγγεγραμμένες που βαίνουν σε ίσα τόξα) (1).
(εγγεγραμμένες που βαίνουν σε ίσα τόξα) (1).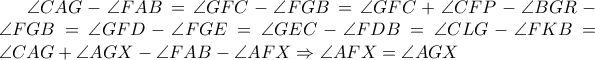 (2) όπου μετά τη δεύτερη ισότητα χρησιμοποιήσαμε την (1) και πριν την συνεπαγωγή το ότι οι γωνίες
(2) όπου μετά τη δεύτερη ισότητα χρησιμοποιήσαμε την (1) και πριν την συνεπαγωγή το ότι οι γωνίες 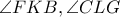 είναι εξωτερικές των τριγώνων
είναι εξωτερικές των τριγώνων 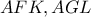 αντίστοιχα.
αντίστοιχα.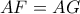 ως ακτίνες του
ως ακτίνες του  άρα
άρα 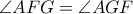 οπότε χρησιμοποιώντας και την (2) είναι
οπότε χρησιμοποιώντας και την (2) είναι 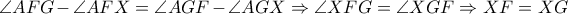 , που όπως εξηγήσαμε, δίνει το ζητούμενο.
, που όπως εξηγήσαμε, δίνει το ζητούμενο.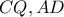 τέμνονται στο
τέμνονται στο 
 τυχαίο σημείο εκτός κύκλου,
τυχαίο σημείο εκτός κύκλου, μια εφαπτομένη του και
μια εφαπτομένη του και 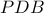 μια τυχαία του τέμνουσα.Τότε ισχύει ότι
μια τυχαία του τέμνουσα.Τότε ισχύει ότι 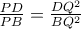 .
.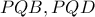 έχουμε
έχουμε 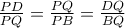
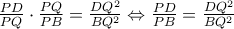 , το ζητούμενο
, το ζητούμενο ορθογώνιο και
ορθογώνιο και  το ύψος προς την υποτείνουσα θα ισχύει ότι
το ύψος προς την υποτείνουσα θα ισχύει ότι 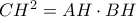 .
. με τέμνουσα την ευθεία
με τέμνουσα την ευθεία 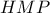 (
( που από υπόθεση βρίσκεται στην
που από υπόθεση βρίσκεται στην 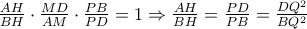 από το λήμμα,οπότε είναι
από το λήμμα,οπότε είναι 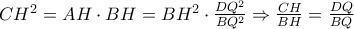 και επειδή
και επειδή 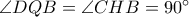 τα τρίγωνα
τα τρίγωνα 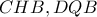 είναι όμοια και άρα κατ επέκταση όμοια είναι και τα τρίγωνα
είναι όμοια και άρα κατ επέκταση όμοια είναι και τα τρίγωνα 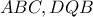 .
.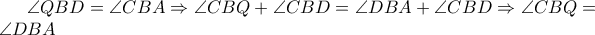 .(1)
.(1)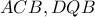 έχουμε
έχουμε 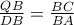 που μαζί με την (1) σημαίνει ότι και τα τρίγωνα
που μαζί με την (1) σημαίνει ότι και τα τρίγωνα 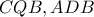 είναι όμοια.
είναι όμοια.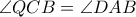 οπότε το τετράπλευρο
οπότε το τετράπλευρο 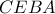 είναι εγγράψιμο.
είναι εγγράψιμο.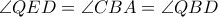 οπότε το τετράπλευρο
οπότε το τετράπλευρο 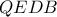 είναι εγγράψιμο,που δίνει το ζητούμενο.
είναι εγγράψιμο,που δίνει το ζητούμενο.