IMO 2016
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
IMO 2016
Ας δούμε εδώ τα θέματα σχετικά με την IMO 2016,τον κορυφαίο διαγωνισμό των μαθηματικών.
Καλή επιτυχία σε όλα τα παιδιά της ελληνικής αποστολής!
Καλή επιτυχία σε όλα τα παιδιά της ελληνικής αποστολής!
Σημαντήρης Γιάννης
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: IMO 2016
Δίνω τα θέματα της πρώτης μέρας του διαγωνισμού. Ευχαριστώ το Ραφαήλ Τσιάμη που μου τα έστειλε.
Πρόβλημα 1
Έστω τρίγωνο ορθογώνιο στο B. Επιλέγουμε σημείο
ορθογώνιο στο B. Επιλέγουμε σημείο  της ευθείας
της ευθείας  ώστε να ισχύει
ώστε να ισχύει  και το
και το  να βρίσκεται στο εσωτερικό του ευθύγραμμου τμήματος
να βρίσκεται στο εσωτερικό του ευθύγραμμου τμήματος  . Επίσης, θεωρούμε σημείο D ώστε
. Επίσης, θεωρούμε σημείο D ώστε  και η
και η  να είναι διχοτόμος της γωνίας
να είναι διχοτόμος της γωνίας  . Επίσης, διαλέγουμε σημείο
. Επίσης, διαλέγουμε σημείο  ώστε
ώστε  και η AD να είναι διχοτόμος της
και η AD να είναι διχοτόμος της  . Αν
. Αν  είναι το μέσον της υποτείνουσας του τριγώνου
είναι το μέσον της υποτείνουσας του τριγώνου  , και
, και  σημείο τέτοιο ώστε το τετράπλευρο
σημείο τέτοιο ώστε το τετράπλευρο  να είναι παραλληλόγραμμο με
να είναι παραλληλόγραμμο με  , να αποδειχτεί ότι οι ευθείες
, να αποδειχτεί ότι οι ευθείες  συντρέχουν.
συντρέχουν.
Πρόβλημα 2
Να βρεθούν όλοι οι θετικοί ακέραιοι , που είναι τέτοιοι ώστε να μπορούν να τοποθετηθούν τα γράμματα Ι,Μ,Ο στον
, που είναι τέτοιοι ώστε να μπορούν να τοποθετηθούν τα γράμματα Ι,Μ,Ο στον  πίνακα (ένα γράμμα σε κάθε κελί), ώστε να ισχύουν οι συνθήκες:
πίνακα (ένα γράμμα σε κάθε κελί), ώστε να ισχύουν οι συνθήκες:
1) Σε κάθε γραμμή και στήλη του πίνακα να υπάρχει ίσος αριθμός από Ι,Μ,Ο.
2) Αν ο αριθμός των κελιών σε μία διαγώνιο είναι πολλαπλάσιο του 3, τότε έχουμε ίσο αριθμό από Ι,Μ,Ο.
Σημείωση: Οι γραμμές και οι στήλες του πίνακα αριθμούνται με αριθμούς από το 1 ως το κατά τη φυσική τους σειρά. Όταν
κατά τη φυσική τους σειρά. Όταν  , ο πίνακας αυτός έχει συνολικά
, ο πίνακας αυτός έχει συνολικά  διαγωνίους, οι οποίες είναι δύο τύπων. Μια διαγώνιος του πρώτου τύπου αποτελείται από κελιά
διαγωνίους, οι οποίες είναι δύο τύπων. Μια διαγώνιος του πρώτου τύπου αποτελείται από κελιά  για τα οποία το άθροισμα
για τα οποία το άθροισμα  είναι σταθερό, ενώ μια διαγώνιος του δεύτερου τύπου αποτελείται από κελιά
είναι σταθερό, ενώ μια διαγώνιος του δεύτερου τύπου αποτελείται από κελιά  για τα οποία η διαφορά
για τα οποία η διαφορά  είναι σταθερή.
είναι σταθερή.
Πρόβλημα 3
'Εστω ένα κυρτό πολύγωνο, του οποίου οι κορυφές βρίσκονται σε κύκλο και έχουν ακέραιες συντεταγμένες. Έστω
ένα κυρτό πολύγωνο, του οποίου οι κορυφές βρίσκονται σε κύκλο και έχουν ακέραιες συντεταγμένες. Έστω  ένας περιττός θετικός ακέραιος, ο οποίος δίνεται ότι διαιρεί τα τετράγωνα των μηκών των πλευρών του πολυγώνου. Να αποδειχτεί ότι το διπλάσιο του εμβαδού του πολυγώνου είναι θετικός ακέραιος, και ότι διαιρείται από το
ένας περιττός θετικός ακέραιος, ο οποίος δίνεται ότι διαιρεί τα τετράγωνα των μηκών των πλευρών του πολυγώνου. Να αποδειχτεί ότι το διπλάσιο του εμβαδού του πολυγώνου είναι θετικός ακέραιος, και ότι διαιρείται από το  .
.
Edit: Διόρθωση λαθών σε εκφωνήσεις.
Καλή επιτυχία στις ομάδες Ελλάδας και Κύπρου!
Πρόβλημα 1
Έστω τρίγωνο
 ορθογώνιο στο B. Επιλέγουμε σημείο
ορθογώνιο στο B. Επιλέγουμε σημείο  της ευθείας
της ευθείας  ώστε να ισχύει
ώστε να ισχύει  και το
και το  να βρίσκεται στο εσωτερικό του ευθύγραμμου τμήματος
να βρίσκεται στο εσωτερικό του ευθύγραμμου τμήματος  . Επίσης, θεωρούμε σημείο D ώστε
. Επίσης, θεωρούμε σημείο D ώστε  και η
και η  να είναι διχοτόμος της γωνίας
να είναι διχοτόμος της γωνίας  . Επίσης, διαλέγουμε σημείο
. Επίσης, διαλέγουμε σημείο  ώστε
ώστε  και η AD να είναι διχοτόμος της
και η AD να είναι διχοτόμος της  . Αν
. Αν  είναι το μέσον της υποτείνουσας του τριγώνου
είναι το μέσον της υποτείνουσας του τριγώνου  , και
, και  σημείο τέτοιο ώστε το τετράπλευρο
σημείο τέτοιο ώστε το τετράπλευρο  να είναι παραλληλόγραμμο με
να είναι παραλληλόγραμμο με  , να αποδειχτεί ότι οι ευθείες
, να αποδειχτεί ότι οι ευθείες  συντρέχουν.
συντρέχουν.Πρόβλημα 2
Να βρεθούν όλοι οι θετικοί ακέραιοι
 , που είναι τέτοιοι ώστε να μπορούν να τοποθετηθούν τα γράμματα Ι,Μ,Ο στον
, που είναι τέτοιοι ώστε να μπορούν να τοποθετηθούν τα γράμματα Ι,Μ,Ο στον  πίνακα (ένα γράμμα σε κάθε κελί), ώστε να ισχύουν οι συνθήκες:
πίνακα (ένα γράμμα σε κάθε κελί), ώστε να ισχύουν οι συνθήκες:1) Σε κάθε γραμμή και στήλη του πίνακα να υπάρχει ίσος αριθμός από Ι,Μ,Ο.
2) Αν ο αριθμός των κελιών σε μία διαγώνιο είναι πολλαπλάσιο του 3, τότε έχουμε ίσο αριθμό από Ι,Μ,Ο.
Σημείωση: Οι γραμμές και οι στήλες του πίνακα αριθμούνται με αριθμούς από το 1 ως το
 κατά τη φυσική τους σειρά. Όταν
κατά τη φυσική τους σειρά. Όταν  , ο πίνακας αυτός έχει συνολικά
, ο πίνακας αυτός έχει συνολικά  διαγωνίους, οι οποίες είναι δύο τύπων. Μια διαγώνιος του πρώτου τύπου αποτελείται από κελιά
διαγωνίους, οι οποίες είναι δύο τύπων. Μια διαγώνιος του πρώτου τύπου αποτελείται από κελιά  για τα οποία το άθροισμα
για τα οποία το άθροισμα  είναι σταθερό, ενώ μια διαγώνιος του δεύτερου τύπου αποτελείται από κελιά
είναι σταθερό, ενώ μια διαγώνιος του δεύτερου τύπου αποτελείται από κελιά  για τα οποία η διαφορά
για τα οποία η διαφορά  είναι σταθερή.
είναι σταθερή.Πρόβλημα 3
'Εστω
 ένα κυρτό πολύγωνο, του οποίου οι κορυφές βρίσκονται σε κύκλο και έχουν ακέραιες συντεταγμένες. Έστω
ένα κυρτό πολύγωνο, του οποίου οι κορυφές βρίσκονται σε κύκλο και έχουν ακέραιες συντεταγμένες. Έστω  ένας περιττός θετικός ακέραιος, ο οποίος δίνεται ότι διαιρεί τα τετράγωνα των μηκών των πλευρών του πολυγώνου. Να αποδειχτεί ότι το διπλάσιο του εμβαδού του πολυγώνου είναι θετικός ακέραιος, και ότι διαιρείται από το
ένας περιττός θετικός ακέραιος, ο οποίος δίνεται ότι διαιρεί τα τετράγωνα των μηκών των πλευρών του πολυγώνου. Να αποδειχτεί ότι το διπλάσιο του εμβαδού του πολυγώνου είναι θετικός ακέραιος, και ότι διαιρείται από το  .
.Edit: Διόρθωση λαθών σε εκφωνήσεις.
Καλή επιτυχία στις ομάδες Ελλάδας και Κύπρου!
τελευταία επεξεργασία από jason.prod σε Δευ Ιούλ 11, 2016 5:02 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Προδρομίδης Κυπριανός-Ιάσων
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: IMO 2016
Καλό! Η απάντηση είναι όλα τα πολλαπλάσια τουjasonmaths4ever έγραψε: Πρόβλημα 2
Να βρεθούν όλοι οι θετικοί ακέραιοι, που είναι τέτοιοι ώστε να μπορούν να τοποθετηθούν τα γράμματα Ι,Μ,Ο στον
πίνακα (ένα γράμμα σε κάθε κελί), ώστε να ισχύουν οι συνθήκες:
1) Σε κάθε γραμμή και στήλη του πίνακα να υπάρχει ίσος αριθμός από Ι,Μ,Ο.
2) Αν ο αριθμός των κελιών σε μία διαγώνιο είναι πολλαπλάσιο του 3, τότε έχουμε ίσο αριθμό από Ι,Μ,Ο.
Σημείωση: Οι γραμμές και οι στήλες του πίνακα αριθμούνται με αριθμούς από το 1 ως τοκατά τη φυσική τους σειρά. Όταν
, ο πίνακας αυτός έχει συνολικά
διαγωνίους, οι οποίες είναι δύο τύπων. Μια διαγώνιος του πρώτου τύπου αποτελείται από κελιά
για τα οποία το άθροισμα
είναι σταθερό, ενώ μια διαγώνιος του δεύτερου τύπου αποτελείται από κελιά
για τα οποία η διαφορά
είναι σταθερή.
 .
. Είναι προφανές ότι
 . Μετράμε με πολλαπλότητα όλα τα κελιά που βρίσκονται στις σειρές της μορφής
. Μετράμε με πολλαπλότητα όλα τα κελιά που βρίσκονται στις σειρές της μορφής  , τις στήλες της μορφής
, τις στήλες της μορφής  , όλες τις διαγωνίους με πλήθος κελιών πολλαπλάσιο του
, όλες τις διαγωνίους με πλήθος κελιών πολλαπλάσιο του  , και αφαιρούμε τα κελιά που βρίσκονται στις στήλες/σειρές της μορφής
, και αφαιρούμε τα κελιά που βρίσκονται στις στήλες/σειρές της μορφής  .
.Παρατηρούμε ότι μετρήσαμε όλα τα κελιά της μορφής
 με
με  και
και  από τρεις φορές το κάθε ένα. (Δεν μετρήθηκε κανένα άλλο κελί.) Άρα το πλήθος αυτών των κελιών (με πολλαπλότητα) είναι
από τρεις φορές το κάθε ένα. (Δεν μετρήθηκε κανένα άλλο κελί.) Άρα το πλήθος αυτών των κελιών (με πολλαπλότητα) είναι  . Σε αυτά τα κελιά υπάρχει ίσως αριθμός από
. Σε αυτά τα κελιά υπάρχει ίσως αριθμός από  οπότε σε αυτά τα κελία υπάρχουν
οπότε σε αυτά τα κελία υπάρχουν  από κάθε ένα από τα
από κάθε ένα από τα  . Όμως κάθε ένα από αυτά είναι πολλαπλάσιο του
. Όμως κάθε ένα από αυτά είναι πολλαπλάσιο του  αφού κάθε κελί μετρήθηκε τρεις φορές (ή μηδέν). Άρα έχουμε
αφού κάθε κελί μετρήθηκε τρεις φορές (ή μηδέν). Άρα έχουμε  και άρα
και άρα  .
.Μένει τώρα να κάνουμε την κατασκευή. Για
 παίρνω την πιο κάτω κατασκευή:
παίρνω την πιο κάτω κατασκευή:
Για
 ξεκινώ από ένα
ξεκινώ από ένα 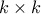 πίνακα και σε κάθε κελί του τοποθετώ την πιο πάνω κατασκευή. Δεν είναι δύσκολο να δούμε ότι δουλεύει. (Επειδή κάθε διαγώνιος με πλήθος κελιών πολλαπλάσιου του
πίνακα και σε κάθε κελί του τοποθετώ την πιο πάνω κατασκευή. Δεν είναι δύσκολο να δούμε ότι δουλεύει. (Επειδή κάθε διαγώνιος με πλήθος κελιών πολλαπλάσιου του  σπάζει σε κομμάτια από τις
σπάζει σε κομμάτια από τις  κατασκευές με κάθε ένα εκ των οποίων να έχει πλήθος κελιών πολλαπλάσιο του
κατασκευές με κάθε ένα εκ των οποίων να έχει πλήθος κελιών πολλαπλάσιο του  και άρα ίσο πλήθος από
και άρα ίσο πλήθος από  .)
.)-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
Re: IMO 2016
Πρόβλημα 1
Ωραίο πρόβλημα με πολλές ιδιότητες, το θέμα είναι να του τις "πάρεις".Ελπίζω η λύση που έκανα να είναι πλήρης
Το νομίζω πρέπει να είναι στην προέκταση της
νομίζω πρέπει να είναι στην προέκταση της  .
.
Είναι προφανές ότι (από ισοσκελή τρίγωνα και διχοτόμους)
Επειδή και
και  άρα τα
άρα τα  συνευθειακά.
συνευθειακά.
Προφανώς τα ισοσκελή με ίσες γωνίες βάσης τρίγωνα είναι όμοια άρα
είναι όμοια άρα  και επειδή
και επειδή  τα τρίγωνα
τα τρίγωνα  είναι επίσης όμοια άρα
είναι επίσης όμοια άρα  .Όμως
.Όμως  και
και  άρα
άρα  οπότε
οπότε  εγγράψιμο άρα
εγγράψιμο άρα  άρα
άρα  διχοτόμος της
διχοτόμος της  άρα
άρα  έγκεντρο τριγώνου
έγκεντρο τριγώνου  .
.
Επιπλέον (αφού μέσο υποτείνουσας ορθογωνίου
μέσο υποτείνουσας ορθογωνίου  ) εύκολα
) εύκολα  άρα και το
άρα και το  εγγράψιμο οπότε
εγγράψιμο οπότε  άρα είναι
άρα είναι  και
και  οπότε τα τρίγωνα
οπότε τα τρίγωνα  όμοια.(1)
όμοια.(1)
Προφανώς τα ισοσκελή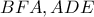 όμοια άρα
όμοια άρα  οπότε εύκολα τα
οπότε εύκολα τα  όμοια άρα από (1) τα
όμοια άρα από (1) τα  όμοια άρα
όμοια άρα  άρα τα
άρα τα 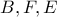 συνευθειακά.
συνευθειακά.
Τώρα εύκολα προκύπτει η ισότητα των πάνω τριγώνων άρα άρα τα
άρα τα  και
και  παραλληλόγραμμα (γιατί?)
παραλληλόγραμμα (γιατί?)
Εύκολα με κυνήγι γωνιών τώρα άρα το
άρα το  προκύπτει ισοσκελές τραπέζιο.
προκύπτει ισοσκελές τραπέζιο.
Έστω τώρα ότι οι τέμνονται στο
τέμνονται στο  .Τότε
.Τότε 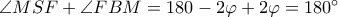 άρα το
άρα το  εγγράψιμο.Τότε όμως αφού
εγγράψιμο.Τότε όμως αφού 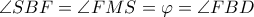 τα
τα  συνευθειακά και η απόδειξη ολοκληρώνεται.
συνευθειακά και η απόδειξη ολοκληρώνεται.
Σημ.Στο κυνηγι των γωνιών μπορεί να βοηθήσει και το εγγράψιμο που προκύπτει από το θεώρημα του Νοτόυ Πόλου στο τρίγωνο
που προκύπτει από το θεώρημα του Νοτόυ Πόλου στο τρίγωνο  .
.
έντιτ:προσθήκη σχήματος
Ωραίο πρόβλημα με πολλές ιδιότητες, το θέμα είναι να του τις "πάρεις".Ελπίζω η λύση που έκανα να είναι πλήρης
Το
 νομίζω πρέπει να είναι στην προέκταση της
νομίζω πρέπει να είναι στην προέκταση της  .
.Είναι προφανές ότι (από ισοσκελή τρίγωνα και διχοτόμους)

Επειδή
 και
και  άρα τα
άρα τα  συνευθειακά.
συνευθειακά.Προφανώς τα ισοσκελή με ίσες γωνίες βάσης τρίγωνα
 είναι όμοια άρα
είναι όμοια άρα  και επειδή
και επειδή  τα τρίγωνα
τα τρίγωνα  είναι επίσης όμοια άρα
είναι επίσης όμοια άρα  .Όμως
.Όμως  και
και  άρα
άρα  οπότε
οπότε  εγγράψιμο άρα
εγγράψιμο άρα  άρα
άρα  διχοτόμος της
διχοτόμος της  άρα
άρα  έγκεντρο τριγώνου
έγκεντρο τριγώνου  .
.Επιπλέον (αφού
 μέσο υποτείνουσας ορθογωνίου
μέσο υποτείνουσας ορθογωνίου  ) εύκολα
) εύκολα  άρα και το
άρα και το  εγγράψιμο οπότε
εγγράψιμο οπότε  άρα είναι
άρα είναι  και
και  οπότε τα τρίγωνα
οπότε τα τρίγωνα  όμοια.(1)
όμοια.(1)Προφανώς τα ισοσκελή
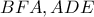 όμοια άρα
όμοια άρα  οπότε εύκολα τα
οπότε εύκολα τα  όμοια άρα από (1) τα
όμοια άρα από (1) τα  όμοια άρα
όμοια άρα  άρα τα
άρα τα 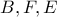 συνευθειακά.
συνευθειακά.Τώρα εύκολα προκύπτει η ισότητα των πάνω τριγώνων άρα
 άρα τα
άρα τα  και
και  παραλληλόγραμμα (γιατί?)
παραλληλόγραμμα (γιατί?)Εύκολα με κυνήγι γωνιών τώρα
 άρα το
άρα το  προκύπτει ισοσκελές τραπέζιο.
προκύπτει ισοσκελές τραπέζιο.Έστω τώρα ότι οι
 τέμνονται στο
τέμνονται στο  .Τότε
.Τότε 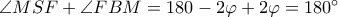 άρα το
άρα το  εγγράψιμο.Τότε όμως αφού
εγγράψιμο.Τότε όμως αφού 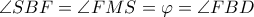 τα
τα  συνευθειακά και η απόδειξη ολοκληρώνεται.
συνευθειακά και η απόδειξη ολοκληρώνεται.Σημ.Στο κυνηγι των γωνιών μπορεί να βοηθήσει και το εγγράψιμο
 που προκύπτει από το θεώρημα του Νοτόυ Πόλου στο τρίγωνο
που προκύπτει από το θεώρημα του Νοτόυ Πόλου στο τρίγωνο  .
.έντιτ:προσθήκη σχήματος
τελευταία επεξεργασία από simantiris j. σε Δευ Ιούλ 11, 2016 8:25 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Σημαντήρης Γιάννης
Re: IMO 2016
Εδώ υποθέτω λείπει η πληροφορία ότι το κέντρο του κύκλου είναι τοjasonmaths4ever έγραψε: Πρόβλημα 3
'Εστωένα κυρτό πολύγωνο, του οποίου οι κορυφές βρίσκονται σε κύκλο και έχουν ακέραιες συντεταγμένες. Έστω
ένας περιττός θετικός ακέραιος, ο οποίος δίνεται ότι διαιρεί τα τετράγωνα των μηκών των πλευρών του πολυγώνου. Να αποδειχτεί ότι το εμβαδόν του πολυγώνου είναι θετικός ακέραιος, και ότι το διπλάσιό του (αριθμητικά) διαιρείται από το
.
 . Φυσικά δεν έχουν όλα τα τρίγωνα με ακέραιες συντεταγμένες κορυφών ακέραιο εμβαδόν (μπορεί να θεωρηθεί
. Φυσικά δεν έχουν όλα τα τρίγωνα με ακέραιες συντεταγμένες κορυφών ακέραιο εμβαδόν (μπορεί να θεωρηθεί  ).
).Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: IMO 2016
Καλά αποτελέσματα στην ομάδα της Ελλάδας και των Αδελφών Κυπρίων. Καλή επάνοδο με μετάλλια και προοπτική.
Επιτρέψτε μου ένα σχόλιο: δύο περιπτώσεις, γιατί μιλάει για ευθεία
δύο περιπτώσεις, γιατί μιλάει για ευθεία  και όχι πλευρά
και όχι πλευρά  .
.
Επιτρέψτε μου ένα σχόλιο:
Το πρόβλημα αυτό ήθελε πάνω από όλα μεγάλη οπτική ικανότητα με τις τόσες πολλές γραμμές που έχει άμα τη εμφανίσει στην εκφώνηση (θεωρούμε και ξαναθεωρούμε και πάλι θεωρούμε, μάλλον ο κατασκευαστής εκμεταλεύτηκε full τις δυνατότητες του geogebra). Κατά τα άλλα είναι σίγουρα ένα καλό γεωμετρικό πρόβλημα εκκίνησης. Βέβαια αν είδα καλά και σύμφωνα με την παραπάνω μετάφραση θα πρέπει να διακριθούν για τη θέση τουjasonmaths4ever έγραψε: Πρόβλημα 1
Έστω τρίγωνοορθογώνιο στο B. Επιλέγουμε σημείο
της ευθείας
ώστε να ισχύει
. Επίσης, θεωρούμε σημείο D ώστε
και η
να είναι διχοτόμος της γωνίας
. Επίσης, διαλέγουμε σημείο
ώστε
και η AD να είναι διχοτόμος της
. Αν
είναι το μέσον της υποτείνουσας του τριγώνου
, και
σημείο τέτοιο ώστε το τετράπλευρο
να είναι παραλληλόγραμμο με
, να αποδειχτεί ότι οι ευθείες
συντρέχουν.
 δύο περιπτώσεις, γιατί μιλάει για ευθεία
δύο περιπτώσεις, γιατί μιλάει για ευθεία  και όχι πλευρά
και όχι πλευρά  .
.
τελευταία επεξεργασία από S.E.Louridas σε Δευ Ιούλ 11, 2016 4:21 pm, έχει επεξεργασθεί 5 φορές συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: IMO 2016
ΠΡΟΒΛΗΜΑ 1
Αρκεί να δείξουμε τα εξής:
(a) Τα σημεία ανήκουν σε κύκλο
ανήκουν σε κύκλο  κέντρου
κέντρου 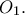
(β) Τα σημεία ανήκουν σε κύκλο
ανήκουν σε κύκλο  κέντρου
κέντρου 
(γ) Τα σημεία ανήκουν σε κύκλο
ανήκουν σε κύκλο  με κέντρο όχι στην
με κέντρο όχι στην  .
.
Τότε οι χορδές και
και  του
του  θα τέμνονται στην κοινή χορδή
θα τέμνονται στην κοινή χορδή  των κύκλων
των κύκλων  και
και 
(Δείτε, π.χ., Evan Chen, Euclidean Geometry in Mathematical Olympiads, pp. 26-28, MAA 2016.)
Πράγματι:
(γ) Παρατηρούμε ότι αν είναι το σημείο τομής της μεσοκαθέτου του
είναι το σημείο τομής της μεσοκαθέτου του  με την
με την  , τότε
, τότε  είναι ρόμβος. Επιπλέον,
είναι ρόμβος. Επιπλέον,  , κι άρα
, κι άρα  ομοκυκλικά. Ανήκουν λοιπόν στον κύκλο κέντρου
ομοκυκλικά. Ανήκουν λοιπόν στον κύκλο κέντρου  , και διαμέτρου
, και διαμέτρου  ( aφού
( aφού  ). Άρα
). Άρα 
Αφού μεσοκάθετος του
μεσοκάθετος του  έπεται
έπεται  , κι άρα το
, κι άρα το  ανήκει στον ίδιο κύκλο.
ανήκει στον ίδιο κύκλο.
Συγκρίνοντας τα ισοσκελή τρίγωνα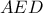 και
και  βλέπουμε ότι είναι ίσα (αφού
βλέπουμε ότι είναι ίσα (αφού  και
και  ) Συνεπώς,
) Συνεπώς,  , κι άρα το
, κι άρα το  ανήκει στον ίδιο κύκλο.
ανήκει στον ίδιο κύκλο.
(β) Το είναι ρόμβος (από την κατασκευή) .Άρα
είναι ρόμβος (από την κατασκευή) .Άρα  . Συνεπώς,
. Συνεπώς,  συνευθειακά και
συνευθειακά και  . Άρα το ισοσκελές τραπέζιο
. Άρα το ισοσκελές τραπέζιο  είναι εγγράψιμο σε κύκλο
είναι εγγράψιμο σε κύκλο  κέντρου
κέντρου 
(a) Ομοίως με το (α), το ισοσκελές τραπέζιο ίναι εγγράψιμο σε κύκλο
ίναι εγγράψιμο σε κύκλο  κέντρου
κέντρου 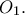
Αλλά και το είναι εγγράψιμο σε κύκλο (angle chasing) κι άρα στον
είναι εγγράψιμο σε κύκλο (angle chasing) κι άρα στον  . Συνεπώς, τα σημεία
. Συνεπώς, τα σημεία  ανήκουν στον κύκλο
ανήκουν στον κύκλο  , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε.
Φιλικά,
Αχιλλέας
Αρκεί να δείξουμε τα εξής:
(a) Τα σημεία
 ανήκουν σε κύκλο
ανήκουν σε κύκλο  κέντρου
κέντρου 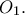
(β) Τα σημεία
 ανήκουν σε κύκλο
ανήκουν σε κύκλο  κέντρου
κέντρου 
(γ) Τα σημεία
 ανήκουν σε κύκλο
ανήκουν σε κύκλο  με κέντρο όχι στην
με κέντρο όχι στην  .
.Τότε οι χορδές
 και
και  του
του  θα τέμνονται στην κοινή χορδή
θα τέμνονται στην κοινή χορδή  των κύκλων
των κύκλων  και
και 
(Δείτε, π.χ., Evan Chen, Euclidean Geometry in Mathematical Olympiads, pp. 26-28, MAA 2016.)
Πράγματι:
(γ) Παρατηρούμε ότι αν
 είναι το σημείο τομής της μεσοκαθέτου του
είναι το σημείο τομής της μεσοκαθέτου του  με την
με την  , τότε
, τότε  είναι ρόμβος. Επιπλέον,
είναι ρόμβος. Επιπλέον,  , κι άρα
, κι άρα  ομοκυκλικά. Ανήκουν λοιπόν στον κύκλο κέντρου
ομοκυκλικά. Ανήκουν λοιπόν στον κύκλο κέντρου  , και διαμέτρου
, και διαμέτρου  ( aφού
( aφού  ). Άρα
). Άρα 
Αφού
 μεσοκάθετος του
μεσοκάθετος του  έπεται
έπεται  , κι άρα το
, κι άρα το  ανήκει στον ίδιο κύκλο.
ανήκει στον ίδιο κύκλο. Συγκρίνοντας τα ισοσκελή τρίγωνα
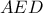 και
και  βλέπουμε ότι είναι ίσα (αφού
βλέπουμε ότι είναι ίσα (αφού  και
και  ) Συνεπώς,
) Συνεπώς,  , κι άρα το
, κι άρα το  ανήκει στον ίδιο κύκλο.
ανήκει στον ίδιο κύκλο. (β) Το
 είναι ρόμβος (από την κατασκευή) .Άρα
είναι ρόμβος (από την κατασκευή) .Άρα  . Συνεπώς,
. Συνεπώς,  συνευθειακά και
συνευθειακά και  . Άρα το ισοσκελές τραπέζιο
. Άρα το ισοσκελές τραπέζιο  είναι εγγράψιμο σε κύκλο
είναι εγγράψιμο σε κύκλο  κέντρου
κέντρου 
(a) Ομοίως με το (α), το ισοσκελές τραπέζιο
 ίναι εγγράψιμο σε κύκλο
ίναι εγγράψιμο σε κύκλο  κέντρου
κέντρου 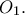
Αλλά και το
 είναι εγγράψιμο σε κύκλο (angle chasing) κι άρα στον
είναι εγγράψιμο σε κύκλο (angle chasing) κι άρα στον  . Συνεπώς, τα σημεία
. Συνεπώς, τα σημεία  ανήκουν στον κύκλο
ανήκουν στον κύκλο  , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε.Φιλικά,
Αχιλλέας
- Συνημμένα
-
- imo_2016_1..png (31.42 KiB) Προβλήθηκε 5813 φορές
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: IMO 2016
Γεια χαρά!S.E.Louridas έγραψε: ...Βέβαια αν είδα καλά και σύμφωνα με την παραπάνω μετάφραση θα πρέπει να διακριθούν για τη θέση τουδύο περιπτώσεις, γιατί μιλάει για ευθεία
και όχι πλευρά
.
Στο αγγλικό κείμενο αναφέρεται ότι το
 βρίσκεται ανάμεσα στα σημεία
βρίσκεται ανάμεσα στα σημεία  .
.-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Re: IMO 2016
Έχετε δίκιο, παράλειψή μου. Συγγνώμη για την ταλαιπωρία.george visvikis έγραψε:Γεια χαρά!S.E.Louridas έγραψε: ...Βέβαια αν είδα καλά και σύμφωνα με την παραπάνω μετάφραση θα πρέπει να διακριθούν για τη θέση τουδύο περιπτώσεις, γιατί μιλάει για ευθεία
και όχι πλευρά
.
Στο αγγλικό κείμενο αναφέρεται ότι τοβρίσκεται ανάμεσα στα σημεία
.
Προδρομίδης Κυπριανός-Ιάσων
Re: IMO 2016
Έκανα λάθος, το κέντρο του κύκλου δεν είναι τοdement έγραψε:Εδώ υποθέτω λείπει η πληροφορία ότι το κέντρο του κύκλου είναι τοjasonmaths4ever έγραψε: Πρόβλημα 3
'Εστωένα κυρτό πολύγωνο, του οποίου οι κορυφές βρίσκονται σε κύκλο και έχουν ακέραιες συντεταγμένες. Έστω
ένας περιττός θετικός ακέραιος, ο οποίος δίνεται ότι διαιρεί τα τετράγωνα των μηκών των πλευρών του πολυγώνου. Να αποδειχτεί ότι το εμβαδόν του πολυγώνου είναι θετικός ακέραιος, και ότι το διπλάσιό του (αριθμητικά) διαιρείται από το
.
. Φυσικά δεν έχουν όλα τα τρίγωνα με ακέραιες συντεταγμένες κορυφών ακέραιο εμβαδόν (μπορεί να θεωρηθεί
).
 , πολύ απλά το πρώτο από τα δύο ερωτήματα (εμβαδόν θετικός ακέραιος) δεν υπάρχει στο αγγλικό.
, πολύ απλά το πρώτο από τα δύο ερωτήματα (εμβαδόν θετικός ακέραιος) δεν υπάρχει στο αγγλικό.Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: IMO 2016
Για το πρόβλημα 1.
 εκεί που ακριβώς υπάρχουν στο σχήμα κάτω.
εκεί που ακριβώς υπάρχουν στο σχήμα κάτω.
Μετά ταύτα η απόδειξη είναι σχεδόν άμεση.
(*) Η παραπάνω διαδικασία επίλυσης είναι η σκέψη που έκανα για να οδηγηθώ στο σχόλιο που ήδη έχω κάνει στη προηγούμενη παρέμβαση μου. Αν λοιπόν δεν έχω κάνει κάποιο λάθος λόγω ταχύτητας, τότε βλέπουμε την αξία της αποδεικτικής διαδικασίας λόγω του μονοσήμαντου μίας ΓΕΩΜΕΤΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ. Θα δούμε βέβαια και την λύση του εισηγητή του προβλήματος για την πρόθεση του να οδηγήσει σε "κατασκευαστική απόδειξη".
Ο λύτης λοιπόν που θα σκεφτεί να κατασκευάσει το σχήμα του προβλήματος ακολουθώντας με κανόνα και διαβήτη τα βήματα της εκφώνησης αντί να χρησιμοποιήσει την γνωστή φράση "έστω ότι είναι ..." , θα οδηγηθεί στο ΜΟΝΑΔΙΚΟ σχήμα που ακολουθεί με βάση τα επιτάγματα της εκφώνησης τοποθετώντας τα επίμαχα σημείαjasonmaths4ever έγραψε: Πρόβλημα 1
Έστω τρίγωνοορθογώνιο στο B. Επιλέγουμε σημείο
της ευθείας
ώστε να ισχύει
και το
να βρίσκεται στο εσωτερικό του ευθύγραμμου τμήματος
. Επίσης, θεωρούμε σημείο D ώστε
και η
να είναι διχοτόμος της γωνίας
. Επίσης, διαλέγουμε σημείο
ώστε
και η AD να είναι διχοτόμος της
. Αν
είναι το μέσον της υποτείνουσας του τριγώνου
, και
σημείο τέτοιο ώστε το τετράπλευρο
να είναι παραλληλόγραμμο με
, να αποδειχτεί ότι οι ευθείες
συντρέχουν.
 εκεί που ακριβώς υπάρχουν στο σχήμα κάτω.
εκεί που ακριβώς υπάρχουν στο σχήμα κάτω. Μετά ταύτα η απόδειξη είναι σχεδόν άμεση.
(*) Η παραπάνω διαδικασία επίλυσης είναι η σκέψη που έκανα για να οδηγηθώ στο σχόλιο που ήδη έχω κάνει στη προηγούμενη παρέμβαση μου. Αν λοιπόν δεν έχω κάνει κάποιο λάθος λόγω ταχύτητας, τότε βλέπουμε την αξία της αποδεικτικής διαδικασίας λόγω του μονοσήμαντου μίας ΓΕΩΜΕΤΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ. Θα δούμε βέβαια και την λύση του εισηγητή του προβλήματος για την πρόθεση του να οδηγήσει σε "κατασκευαστική απόδειξη".
- Συνημμένα
-
- IMO.png (21.48 KiB) Προβλήθηκε 5487 φορές
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: IMO 2016
Βάζω και τα υπόλοιπα 3 προβλήματα του διαγωνισμού.
Πρόβλημα 4. Ενα σύνολο θετικών ακέραιων αριθμών ονομάζεται εύοσμο, αν αυτό περιέχει δύο τουλάχιστον στοιχεία και καθένα από τα στοιχεία του έχει έναν κοινό πρώτο παράγοντα με ένα τουλάχιστον από τα υπόλοιπα στοιχεία του. Έστω . Ποια είναι η ελάχιστη δυνατή τιμή του θετικού ακεραίου
. Ποια είναι η ελάχιστη δυνατή τιμή του θετικού ακεραίου  έτσι ώστε να υπάρχει ένας μη αρνητικός ακέραιος
έτσι ώστε να υπάρχει ένας μη αρνητικός ακέραιος  για τον οποίο το σύνολο
για τον οποίο το σύνολο  είναι εύοσμο;
είναι εύοσμο;
Πρόβλημα 5. Η εξίσωση γράφεται στον πίνακα, με
γράφεται στον πίνακα, με  γραμμικούς παράγοντες σε κάθε μέλος της. Ποια είναι η ελάχιστη δυνατή τιμή του
γραμμικούς παράγοντες σε κάθε μέλος της. Ποια είναι η ελάχιστη δυνατή τιμή του  για την οποία είναι δυνατόν να σβήσουμε ακριβώς
για την οποία είναι δυνατόν να σβήσουμε ακριβώς  από τους
από τους  γραμμικούς παράγοντες των δύο μελών της εξίσωσης έτσι ώστε ένας τουλάχιστον παράγοντας να μείνει σε κάθε μέλος και η εξίσωση που προκύπτει να μην έχει πραγματικές λύσεις;
γραμμικούς παράγοντες των δύο μελών της εξίσωσης έτσι ώστε ένας τουλάχιστον παράγοντας να μείνει σε κάθε μέλος και η εξίσωση που προκύπτει να μην έχει πραγματικές λύσεις;
Πρόβλημα 6. Δίνονται ευθύγραμμα τμήματα στο επίπεδο έται ώστε κάθε δύο από αυτά τέμνονται σε ένα εσωτερικό τους σημείο και δεν υπάρχουν τρία από αυτά που να περνούν από το ίδιο σημείο. Ο Τζέφ πρέπει να διαλέξει ένα άκρο από κάθε ευθύγραμμο τμήμα και να τοποθετήσει ένα βάτραχο σε αυτό, που να κοιτάζει προς το άλλο άκρο του τμήματος. Ύστερα αυτός θα κάνει
ευθύγραμμα τμήματα στο επίπεδο έται ώστε κάθε δύο από αυτά τέμνονται σε ένα εσωτερικό τους σημείο και δεν υπάρχουν τρία από αυτά που να περνούν από το ίδιο σημείο. Ο Τζέφ πρέπει να διαλέξει ένα άκρο από κάθε ευθύγραμμο τμήμα και να τοποθετήσει ένα βάτραχο σε αυτό, που να κοιτάζει προς το άλλο άκρο του τμήματος. Ύστερα αυτός θα κάνει  χειροκροτήματα. Σε κάθε χειροκρότημα, κάθε βάτραχος πηδά αμέσως προς το επόμενο σημείο τομής του ευθυγράμμου τμήματός του. Οι βάτραχοι ποτέ δεν αλλάζουν την κατεύθυνση των πηδημάτων τους. Ο Τζέφ θέλει να τοποθετήσει τους βατράχους κατά τέτοιο τρόπο ώστε να μην συμβεί ποτέ να βρεθούν δύο από αυτούς στο ίδιο σημείο τομής την ίδια χρονική στιγμή.
χειροκροτήματα. Σε κάθε χειροκρότημα, κάθε βάτραχος πηδά αμέσως προς το επόμενο σημείο τομής του ευθυγράμμου τμήματός του. Οι βάτραχοι ποτέ δεν αλλάζουν την κατεύθυνση των πηδημάτων τους. Ο Τζέφ θέλει να τοποθετήσει τους βατράχους κατά τέτοιο τρόπο ώστε να μην συμβεί ποτέ να βρεθούν δύο από αυτούς στο ίδιο σημείο τομής την ίδια χρονική στιγμή.
(α) Να αποδείξετε ότι ο Τζέφ μπορεί πάντοτε να πραγματοποιήσει την επιθυμία του, όταν ο αριθμός είναι περιττός.
είναι περιττός.
(β) Να αποδείξετε ότι ο Τζέφ δεν μπορεί ποτέ να πραγματοποιήσει την επιθυμία του, όταν ο είναι άρτιος.
είναι άρτιος.
Αλέξανδρος
Πρόβλημα 4. Ενα σύνολο θετικών ακέραιων αριθμών ονομάζεται εύοσμο, αν αυτό περιέχει δύο τουλάχιστον στοιχεία και καθένα από τα στοιχεία του έχει έναν κοινό πρώτο παράγοντα με ένα τουλάχιστον από τα υπόλοιπα στοιχεία του. Έστω
 . Ποια είναι η ελάχιστη δυνατή τιμή του θετικού ακεραίου
. Ποια είναι η ελάχιστη δυνατή τιμή του θετικού ακεραίου  έτσι ώστε να υπάρχει ένας μη αρνητικός ακέραιος
έτσι ώστε να υπάρχει ένας μη αρνητικός ακέραιος  για τον οποίο το σύνολο
για τον οποίο το σύνολο  είναι εύοσμο;
είναι εύοσμο;Πρόβλημα 5. Η εξίσωση
 γράφεται στον πίνακα, με
γράφεται στον πίνακα, με  γραμμικούς παράγοντες σε κάθε μέλος της. Ποια είναι η ελάχιστη δυνατή τιμή του
γραμμικούς παράγοντες σε κάθε μέλος της. Ποια είναι η ελάχιστη δυνατή τιμή του  για την οποία είναι δυνατόν να σβήσουμε ακριβώς
για την οποία είναι δυνατόν να σβήσουμε ακριβώς  από τους
από τους  γραμμικούς παράγοντες των δύο μελών της εξίσωσης έτσι ώστε ένας τουλάχιστον παράγοντας να μείνει σε κάθε μέλος και η εξίσωση που προκύπτει να μην έχει πραγματικές λύσεις;
γραμμικούς παράγοντες των δύο μελών της εξίσωσης έτσι ώστε ένας τουλάχιστον παράγοντας να μείνει σε κάθε μέλος και η εξίσωση που προκύπτει να μην έχει πραγματικές λύσεις;Πρόβλημα 6. Δίνονται
 ευθύγραμμα τμήματα στο επίπεδο έται ώστε κάθε δύο από αυτά τέμνονται σε ένα εσωτερικό τους σημείο και δεν υπάρχουν τρία από αυτά που να περνούν από το ίδιο σημείο. Ο Τζέφ πρέπει να διαλέξει ένα άκρο από κάθε ευθύγραμμο τμήμα και να τοποθετήσει ένα βάτραχο σε αυτό, που να κοιτάζει προς το άλλο άκρο του τμήματος. Ύστερα αυτός θα κάνει
ευθύγραμμα τμήματα στο επίπεδο έται ώστε κάθε δύο από αυτά τέμνονται σε ένα εσωτερικό τους σημείο και δεν υπάρχουν τρία από αυτά που να περνούν από το ίδιο σημείο. Ο Τζέφ πρέπει να διαλέξει ένα άκρο από κάθε ευθύγραμμο τμήμα και να τοποθετήσει ένα βάτραχο σε αυτό, που να κοιτάζει προς το άλλο άκρο του τμήματος. Ύστερα αυτός θα κάνει  χειροκροτήματα. Σε κάθε χειροκρότημα, κάθε βάτραχος πηδά αμέσως προς το επόμενο σημείο τομής του ευθυγράμμου τμήματός του. Οι βάτραχοι ποτέ δεν αλλάζουν την κατεύθυνση των πηδημάτων τους. Ο Τζέφ θέλει να τοποθετήσει τους βατράχους κατά τέτοιο τρόπο ώστε να μην συμβεί ποτέ να βρεθούν δύο από αυτούς στο ίδιο σημείο τομής την ίδια χρονική στιγμή.
χειροκροτήματα. Σε κάθε χειροκρότημα, κάθε βάτραχος πηδά αμέσως προς το επόμενο σημείο τομής του ευθυγράμμου τμήματός του. Οι βάτραχοι ποτέ δεν αλλάζουν την κατεύθυνση των πηδημάτων τους. Ο Τζέφ θέλει να τοποθετήσει τους βατράχους κατά τέτοιο τρόπο ώστε να μην συμβεί ποτέ να βρεθούν δύο από αυτούς στο ίδιο σημείο τομής την ίδια χρονική στιγμή.(α) Να αποδείξετε ότι ο Τζέφ μπορεί πάντοτε να πραγματοποιήσει την επιθυμία του, όταν ο αριθμός
 είναι περιττός.
είναι περιττός.(β) Να αποδείξετε ότι ο Τζέφ δεν μπορεί ποτέ να πραγματοποιήσει την επιθυμία του, όταν ο
 είναι άρτιος.
είναι άρτιος.Αλέξανδρος
Αλέξανδρος Συγκελάκης
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: IMO 2016
Παίζει να είναι ένα από τα πιο εύκολα "4" των τελευταίων ετών.cretanman έγραψε:Βάζω και τα υπόλοιπα 3 προβλήματα του διαγωνισμού.
Πρόβλημα 4. Ενα σύνολο θετικών ακέραιων αριθμών ονομάζεται εύοσμο, αν αυτό περιέχει δύο τουλάχιστον στοιχεία και καθένα από τα στοιχεία του έχει έναν κοινό πρώτο παράγοντα με ένα τουλάχιστον από τα υπόλοιπα στοιχεία του. Έστω. Ποια είναι η ελάχιστη δυνατή τιμή του θετικού ακεραίου
έτσι ώστε να υπάρχει ένας μη αρνητικός ακέραιος
για τον οποίο το σύνολο
είναι εύοσμο;
Παρατηρούμε ότι ο
 είναι πάντα περιττός. Επίσης είναι
είναι πάντα περιττός. Επίσης είναι
όπου σε μια από τις ισότητες χρησιμοποιήσαμε ότι
 .
.Με παρόμοιο τρόπο έχουμε

με
 αν και μόνο αν
αν και μόνο αν  . [Πάλι χρησιμοποιήσαμε ότι
. [Πάλι χρησιμοποιήσαμε ότι  .]
.]Ομοίως παίρνω
 με
με  αν και μόνο αν
αν και μόνο αν 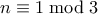
και
 με
με  αν και μόνο αν
αν και μόνο αν 
Ασφαλώς δεν μπορώ να έχω
 αφού
αφού  . Ομοίως δεν μπορώ να έχω
. Ομοίως δεν μπορώ να έχω  αφού ο
αφού ο  δεν έχει κοινό παράγοντα με τους
δεν έχει κοινό παράγοντα με τους  και
και  .
. Δεν μπορώ να έχω ούτε
 . Για να γινόταν αυτό θα έπρεπε ο
. Για να γινόταν αυτό θα έπρεπε ο  να έχει κοινό παράγοντα με τον
να έχει κοινό παράγοντα με τον  και ο
και ο  με τον
με τον  . Αλλά η πρώτη συνθήκη δίνει
. Αλλά η πρώτη συνθήκη δίνει  και η δεύτερη
και η δεύτερη  , άτοπο.
, άτοπο.Δεν μπορώ να έχω ούτε
 . Αν
. Αν  τότε ο
τότε ο  μπορεί να έχει κοινό παράγοντα μόνο με τον
μπορεί να έχει κοινό παράγοντα μόνο με τον  . Τότε
. Τότε  . Αλλά τότε ο
. Αλλά τότε ο  δεν έχει κοινό παράγοντα με κανένα άλλο αριθμό. Αν
δεν έχει κοινό παράγοντα με κανένα άλλο αριθμό. Αν 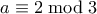 τότε ο
τότε ο  μπορεί να έχει κοινό παράγοντα μόνο με τον
μπορεί να έχει κοινό παράγοντα μόνο με τον  . Πάλι
. Πάλι  και πάλι ο
και πάλι ο  δεν έχει κοινό παράγοντα με κανένα άλλο αριθμό.
δεν έχει κοινό παράγοντα με κανένα άλλο αριθμό. Τέλος μπορώ να έχω
 αρκεί να πάρω
αρκεί να πάρω 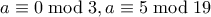 και
και  . Τότε ο
. Τότε ο  έχει κοινό παράγοντα με τον
έχει κοινό παράγοντα με τον  , o
, o  με τον
με τον  και ο
και ο  με τον
με τον  .
.Ασφαλώς μπορώ να πάρω τέτοιον
 από το κινέζικο θεώρημα.
από το κινέζικο θεώρημα.-
nickthegreek
- Δημοσιεύσεις: 412
- Εγγραφή: Δευ Μαρ 01, 2010 2:07 pm
Re: IMO 2016
Ενδιαφέρουσα IMO! Δίνω μια σκέψη λίγο διαφορετική για το  αλλά στα ίδια μήκη κύματος με του Δημήτρη.
αλλά στα ίδια μήκη κύματος με του Δημήτρη.
Υποθέτουμε ότι η κατασκευή είναι εφικτή για δεδομένο . Θα δείξουμε ότι
. Θα δείξουμε ότι  .
.
Ας γράψουμε και ας χωρίσουμε τον πίνακά μας σε
και ας χωρίσουμε τον πίνακά μας σε  τετράγωνα
τετράγωνα  . Κοιτάζουμε τα κέντρα του κάθε τετραγώνου, συνολικά
. Κοιτάζουμε τα κέντρα του κάθε τετραγώνου, συνολικά  στο πλήθος και τα χρωματίζουμε κόκκινα (τα υπόλοιπα τα θεωρώ άσπρα) .
στο πλήθος και τα χρωματίζουμε κόκκινα (τα υπόλοιπα τα θεωρώ άσπρα) .
Παρατηρούμε ότι αν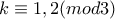 υπάρχει τουλάχιστον ένα γράμμα το οποίο εμφανίζεται περισσότερες φορές από οποιοδήποτε άλλο στα κόκκινα τετράγωνα.
υπάρχει τουλάχιστον ένα γράμμα το οποίο εμφανίζεται περισσότερες φορές από οποιοδήποτε άλλο στα κόκκινα τετράγωνα.
Τώρα παρατηρούμε ότι κάθε κόκκινο τετράγωνο ανήκει ακριβώς σε μια γραμμή, μια στήλη και δύο διαγωνίους. Τέλος, υπάρχει τρόπος να συσχετίσω με τρόπο κάθε γράμμα σε ένα κόκκινο τετράγωνο με τα δύο διαφορετικά του γράμματα σε άσπρα τετράγωνα στην εν λόγω γραμμή. Το ίδιο μπορώ να κάνω και για τη στήλη και για κάθε μια από τις δύο διαγωνίους στις οποίες ανήκει το κόκκινο τετράγωνο (δηλαδή, τελικά, αντιστοιχώ με τρόπο
κάθε γράμμα σε ένα κόκκινο τετράγωνο με τα δύο διαφορετικά του γράμματα σε άσπρα τετράγωνα στην εν λόγω γραμμή. Το ίδιο μπορώ να κάνω και για τη στήλη και για κάθε μια από τις δύο διαγωνίους στις οποίες ανήκει το κόκκινο τετράγωνο (δηλαδή, τελικά, αντιστοιχώ με τρόπο  σε κάθε κόκκινο τετράγωνο
σε κάθε κόκκινο τετράγωνο  άσπρα και αυτά μαζί όλα καλύπτουν ολόκληρο τον πίνακα).
άσπρα και αυτά μαζί όλα καλύπτουν ολόκληρο τον πίνακα).
Για κάθε λοιπόν που εμφανίζεται μια φορά σε κόκκινο τετράγωνο υπάρχουν
λοιπόν που εμφανίζεται μια φορά σε κόκκινο τετράγωνο υπάρχουν 
 και
και  που αντιστοιχούν σε αυτό (και ομοίως κυκλικά για τα
που αντιστοιχούν σε αυτό (και ομοίως κυκλικά για τα  ) . Δεδομένου ότι πρέπει να έχουμε συνολικά ίσο αριθμό από
) . Δεδομένου ότι πρέπει να έχουμε συνολικά ίσο αριθμό από  εύκολα βλέπουμε ότι στα κόκκινα τετράγωνα συνολικά πρέπει να υπάρχει ίσος αριθμός από κάθε γράμμα, που σημαίνει ότι
εύκολα βλέπουμε ότι στα κόκκινα τετράγωνα συνολικά πρέπει να υπάρχει ίσος αριθμός από κάθε γράμμα, που σημαίνει ότι  . Για το ότι τα πολλαπλάσια του
. Για το ότι τα πολλαπλάσια του  είναι λύσεις, όπως ο Δημήτρης.
είναι λύσεις, όπως ο Δημήτρης.
Φιλικά,
Νίκος
 αλλά στα ίδια μήκη κύματος με του Δημήτρη.
αλλά στα ίδια μήκη κύματος με του Δημήτρη. Υποθέτουμε ότι η κατασκευή είναι εφικτή για δεδομένο
 . Θα δείξουμε ότι
. Θα δείξουμε ότι  .
.Ας γράψουμε
 και ας χωρίσουμε τον πίνακά μας σε
και ας χωρίσουμε τον πίνακά μας σε  τετράγωνα
τετράγωνα  . Κοιτάζουμε τα κέντρα του κάθε τετραγώνου, συνολικά
. Κοιτάζουμε τα κέντρα του κάθε τετραγώνου, συνολικά  στο πλήθος και τα χρωματίζουμε κόκκινα (τα υπόλοιπα τα θεωρώ άσπρα) .
στο πλήθος και τα χρωματίζουμε κόκκινα (τα υπόλοιπα τα θεωρώ άσπρα) . Παρατηρούμε ότι αν
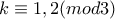 υπάρχει τουλάχιστον ένα γράμμα το οποίο εμφανίζεται περισσότερες φορές από οποιοδήποτε άλλο στα κόκκινα τετράγωνα.
υπάρχει τουλάχιστον ένα γράμμα το οποίο εμφανίζεται περισσότερες φορές από οποιοδήποτε άλλο στα κόκκινα τετράγωνα. Τώρα παρατηρούμε ότι κάθε κόκκινο τετράγωνο ανήκει ακριβώς σε μια γραμμή, μια στήλη και δύο διαγωνίους. Τέλος, υπάρχει τρόπος να συσχετίσω με τρόπο
 κάθε γράμμα σε ένα κόκκινο τετράγωνο με τα δύο διαφορετικά του γράμματα σε άσπρα τετράγωνα στην εν λόγω γραμμή. Το ίδιο μπορώ να κάνω και για τη στήλη και για κάθε μια από τις δύο διαγωνίους στις οποίες ανήκει το κόκκινο τετράγωνο (δηλαδή, τελικά, αντιστοιχώ με τρόπο
κάθε γράμμα σε ένα κόκκινο τετράγωνο με τα δύο διαφορετικά του γράμματα σε άσπρα τετράγωνα στην εν λόγω γραμμή. Το ίδιο μπορώ να κάνω και για τη στήλη και για κάθε μια από τις δύο διαγωνίους στις οποίες ανήκει το κόκκινο τετράγωνο (δηλαδή, τελικά, αντιστοιχώ με τρόπο  σε κάθε κόκκινο τετράγωνο
σε κάθε κόκκινο τετράγωνο  άσπρα και αυτά μαζί όλα καλύπτουν ολόκληρο τον πίνακα).
άσπρα και αυτά μαζί όλα καλύπτουν ολόκληρο τον πίνακα). Για κάθε
 λοιπόν που εμφανίζεται μια φορά σε κόκκινο τετράγωνο υπάρχουν
λοιπόν που εμφανίζεται μια φορά σε κόκκινο τετράγωνο υπάρχουν 
 και
και  που αντιστοιχούν σε αυτό (και ομοίως κυκλικά για τα
που αντιστοιχούν σε αυτό (και ομοίως κυκλικά για τα  ) . Δεδομένου ότι πρέπει να έχουμε συνολικά ίσο αριθμό από
) . Δεδομένου ότι πρέπει να έχουμε συνολικά ίσο αριθμό από  εύκολα βλέπουμε ότι στα κόκκινα τετράγωνα συνολικά πρέπει να υπάρχει ίσος αριθμός από κάθε γράμμα, που σημαίνει ότι
εύκολα βλέπουμε ότι στα κόκκινα τετράγωνα συνολικά πρέπει να υπάρχει ίσος αριθμός από κάθε γράμμα, που σημαίνει ότι  . Για το ότι τα πολλαπλάσια του
. Για το ότι τα πολλαπλάσια του  είναι λύσεις, όπως ο Δημήτρης.
είναι λύσεις, όπως ο Δημήτρης.Φιλικά,
Νίκος
Νίκος Αθανασίου
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: IMO 2016
Εδώ υπάρχουν καινούργια αποτελέσματα.
Ο CYP1 λογικά πρέπει να έχει 7 στο P4. Δεν ξέρω όμως για αυτά που λείπουν από τους υπόλοιπους.
Ο CYP1 λογικά πρέπει να έχει 7 στο P4. Δεν ξέρω όμως για αυτά που λείπουν από τους υπόλοιπους.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες


