Θέματα της δεύτερης φάσης (τελικής) για την 9η τάξη.
1. Δίνονται τρία δευτεροβάθμια τριώνυμα
 που δεν έχουν ρίζες. Οι συντελεστές των μεγιστοβάθμιων όρων τους είναι ίσοι μεταξύ τους, αλλά όλοι οι συντελεστές του
που δεν έχουν ρίζες. Οι συντελεστές των μεγιστοβάθμιων όρων τους είναι ίσοι μεταξύ τους, αλλά όλοι οι συντελεστές του  διαφορετικοί. Να αποδείξετε ότι υπάρχει αριθμός
διαφορετικοί. Να αποδείξετε ότι υπάρχει αριθμός  , τέτοιος ώστε οι εξισώσεις
, τέτοιος ώστε οι εξισώσεις και
και 
να έχουν κοινή ρίζα.
2. Σε πίνακα
 είναι τοποθετημένοι πύργοι (σκακιστικοί), έτσι ώστε όλος ο πίνακας να είναι υπό την απειλή τους και κάθε πύργος να απειλεί το πολύ έναν άλλο πύργο. Ποιο είναι το ελάχιστο
είναι τοποθετημένοι πύργοι (σκακιστικοί), έτσι ώστε όλος ο πίνακας να είναι υπό την απειλή τους και κάθε πύργος να απειλεί το πολύ έναν άλλο πύργο. Ποιο είναι το ελάχιστο  για το οποίο μπορούμε με βεβαιότητα να αποφανθούμε ότι κάθε τετράγωνο
για το οποίο μπορούμε με βεβαιότητα να αποφανθούμε ότι κάθε τετράγωνο 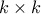 θα περιέχει ένα πύργο;
θα περιέχει ένα πύργο;3. Στην πλευρά
 μη ισοσκελούς τριγώνου
μη ισοσκελούς τριγώνου  δίνονται δυο σημεία
δίνονται δυο σημεία  και
και  τέτοια, ώστε
τέτοια, ώστε  και
και 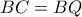 . Η μεσοκάθετος του τμήματος
. Η μεσοκάθετος του τμήματος  τέμνει την διχοτόμο της γωνίας
τέμνει την διχοτόμο της γωνίας  στο σημείο
στο σημείο  (εσωτερικά του τριγώνου). Να αποδείξετε ότι
(εσωτερικά του τριγώνου). Να αποδείξετε ότι .
. 4. Δυο διαφορετικοί πρώτοι αριθμοί
 και
και  έχουν λόγο μικρότερο του δυο. Να αποδείξετε, ότι υπάρχουν δυο διαδοχικοί φυσικοί αριθμοί τέτοιοι, ώστε ο ένας από αυτούς να έχει μέγιστο πρώτο διαιρέτη τον
έχουν λόγο μικρότερο του δυο. Να αποδείξετε, ότι υπάρχουν δυο διαδοχικοί φυσικοί αριθμοί τέτοιοι, ώστε ο ένας από αυτούς να έχει μέγιστο πρώτο διαιρέτη τον  και ο άλλος τον
και ο άλλος τον  .
.Καταληκτική αίθουσα (*)
5. Ο Κώστας και ο Γρηγόρης παίζουν ένα παιχνίδι με μια λευκή ταινία μήκους 2016 κελιών. Ο Κώστας (παίζει πρώτος) με μια κίνηση πρέπει να χρωματίσει μαύρα δυο γειτονικά λευκά κελιά. Ο Γρηγόρης με μια κίνηση πρέπει να χρωματίσει είτε ένα λευκό κελί, είτε τρία γειτονικά λευκά κελιά. Απαγορεύεται να κάνουν κίνηση, με την οποία προκύπτει λευκό κελί που δεν έχει γειτονικά λευκά κελιά. Χάνει αυτός που δεν μπορεί να κάνει κίνηση. Ωστόσο, αν όλα τα κελιά είναι χρωματισμένα, κερδίζει ο Κώστας. Ποιος κερδίζει αν παίξει σωστά (έχει στρατηγική νίκης);
6. Ο εγγεγραμμένος κύκλος τριγώνου
 εφάπτεται της πλευράς
εφάπτεται της πλευράς  στο σημείο
στο σημείο  . Το τμήμα
. Το τμήμα  τέμνει εκ νέου τον κύκλο στο σημείο
τέμνει εκ νέου τον κύκλο στο σημείο  . Τα σημεία
. Τα σημεία  και
και  του εγγεγραμμένου ύκλου είναι τέτοια, ώστε
του εγγεγραμμένου ύκλου είναι τέτοια, ώστε  και
και  . Να αποδείξετε ότι το τμήμα που συνδέει τα κέντρα των εγγεγραμμένων κύκλων των τριγώνων
. Να αποδείξετε ότι το τμήμα που συνδέει τα κέντρα των εγγεγραμμένων κύκλων των τριγώνων  και
και  , διχοτομείται από την διχοτόμο της γωνίας
, διχοτομείται από την διχοτόμο της γωνίας  .
.7. Μια ακολουθία
 διαδοχικών θετικών ακεραίων ονομάζεται «καλή», αν το γινόμενο δυο από αυτών διαιρείται με το άθροισμα των υπόλοιπων. Για ποιά
διαδοχικών θετικών ακεραίων ονομάζεται «καλή», αν το γινόμενο δυο από αυτών διαιρείται με το άθροισμα των υπόλοιπων. Για ποιά  υπάρχουν άπειρες καλές ακολουθίες;
υπάρχουν άπειρες καλές ακολουθίες;(*) Όσοι έλυσαν τρία από τα τέσσερα αρχικά προβλήματα καλέστηκαν να λύσουν άλλα τρία σε διαφορετική αίθουσα. Ο επιπλέον χρόνος που δίνεται είναι μια ώρα.
Στατιστικά: Στον πρώτο πίνακα αναγράφεται ο αριθμός των λυτών ανά θέμα (πόσοι έλυσαν το πρώτο, δύτερο θέμα κτλ.). Στον δεύτερο πίνακα ο αριθμός των μαθητών ανά πλήθος θεμάτων που έλυσαν(πόσοι έλυσαν ένα, δυο κτλ θέματα).



 το οποίο θα βρίσκεται πάνω στη διχοτόμο
το οποίο θα βρίσκεται πάνω στη διχοτόμο  . Η
. Η  θα είναι διχοτόμος της γωνίας
θα είναι διχοτόμος της γωνίας 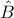 και επειδή το τρίγωνο
και επειδή το τρίγωνο  είναι ισοσκελές, η
είναι ισοσκελές, η  , άρα
, άρα  (1). Ομοίως η
(1). Ομοίως η  θα είναι διχοτόμος της γωνίας
θα είναι διχοτόμος της γωνίας  και επειδή το τρίγωνο
και επειδή το τρίγωνο  είναι ισοσκελές, η
είναι ισοσκελές, η  , άρα
, άρα  (2). Από τις σχέσεις (1) και (2) προκύπτει ότι
(2). Από τις σχέσεις (1) και (2) προκύπτει ότι  , δηλαδή το σημείο
, δηλαδή το σημείο  . Όμως επειδή το σημείο
. Όμως επειδή το σημείο  ,
, 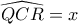 ,
,  και
και 
 , άρα το σημείο
, άρα το σημείο  . Άρα η γωνία
. Άρα η γωνία  είναι η αντίστοιχη επίκεντρη της εγγεγραμμένης γωνίας
είναι η αντίστοιχη επίκεντρη της εγγεγραμμένης γωνίας  και θα ισχύει ότι
και θα ισχύει ότι  .
. , άρα
, άρα  .
. , άρα
, άρα  .
. έχουμε
έχουμε 
 , λόγω των υποθέσεων, είναι πρώτου βαθμού, επομένως έχει μοναδική λύση, έστω τον αριθμό
, λόγω των υποθέσεων, είναι πρώτου βαθμού, επομένως έχει μοναδική λύση, έστω τον αριθμό  .
.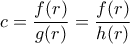 απαντάει στο ζητούμενο.
απαντάει στο ζητούμενο. .
. . Όλοι αυτοί αφήνουν διαφορετικό υπόλοιπό όταν διαιρεθούν με τον
. Όλοι αυτοί αφήνουν διαφορετικό υπόλοιπό όταν διαιρεθούν με τον  άφηναν το ίδιο υπόλοιπο τότε θα είχαμε
άφηναν το ίδιο υπόλοιπο τότε θα είχαμε  και άρα
και άρα  οπότε και
οπότε και  αφού
αφού  .
. ώστε
ώστε  .
. . Κοιτάζουμε τους
. Κοιτάζουμε τους 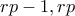 . Ο
. Ο  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  . Άρα ο
. Άρα ο  αφού
αφού 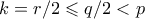 .
.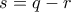 ο οποίος είναι άρτιος αφού αναγκαστικά ο
ο οποίος είναι άρτιος αφού αναγκαστικά ο  . Κοιτάζουμε τους
. Κοιτάζουμε τους  . Ο
. Ο  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  . Άρα ο
. Άρα ο 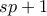 . Επιπλέον ο
. Επιπλέον ο  αφού
αφού  .
. όλες οι ακολουθίες τεσσάρων διαδοχικών φυσικών που ξεκινάνε από περιττό είναι «καλές».
όλες οι ακολουθίες τεσσάρων διαδοχικών φυσικών που ξεκινάνε από περιττό είναι «καλές». ,
,  το γινόμενο
το γινόμενο  διαιρείται
διαιρείται  για κάθε
για κάθε 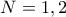 προφανώς δεν γίνεται. Για
προφανώς δεν γίνεται. Για 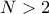 θα δείξουμε ότι υπάρχουν άπειρες καλές ακολουθίες αν και μόνο αν ο
θα δείξουμε ότι υπάρχουν άπειρες καλές ακολουθίες αν και μόνο αν ο  άρτιος. Θεωρούμε την ακολουθία
άρτιος. Θεωρούμε την ακολουθία  . Ξεχωρίζουμε τους
. Ξεχωρίζουμε τους 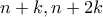 . Το γινόμενό τους ισούται με
. Το γινόμενό τους ισούται με  . Το άθροισμα των υπολοίπων ισούται με
. Το άθροισμα των υπολοίπων ισούται με  . Αν λοιπόν έχουμε επιπλέον ότι
. Αν λοιπόν έχουμε επιπλέον ότι 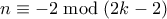 τότε το
τότε το  διαιρεί το
διαιρεί το  περιττός. Αν υπάρχουν άπειρες καλές ακολουθίες τότε υπάρχει σίγουρα και μια καλή ακολουθία της μορφής
περιττός. Αν υπάρχουν άπειρες καλές ακολουθίες τότε υπάρχει σίγουρα και μια καλή ακολουθία της μορφής  με
με  . (Αυτό το
. (Αυτό το  επιλέχθηκε κατάλληλα ώστε να καταλήξουμε σε άτοπο αργότερα. Στο πρόχειρό μου πήρα
επιλέχθηκε κατάλληλα ώστε να καταλήξουμε σε άτοπο αργότερα. Στο πρόχειρό μου πήρα  και βρήκα μια τιμή του
και βρήκα μια τιμή του  η οποία να δίνει άτοπο. Θα μπορούσα με περισσότερη προσοχή να βρω και κάτι μικρότερο του
η οποία να δίνει άτοπο. Θα μπορούσα με περισσότερη προσοχή να βρω και κάτι μικρότερο του 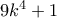 αλλά δεν το έπραξα διότι απλά με ενδιέφερε να καταλήξω στο άτοπο.)
αλλά δεν το έπραξα διότι απλά με ενδιέφερε να καταλήξω στο άτοπο.) ώστε το
ώστε το  να διαιρεί το
να διαιρεί το  .
.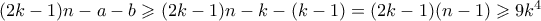 . Οπότε για τους μέγιστους κοινούς διαιρέτες έχουμε
. Οπότε για τους μέγιστους κοινούς διαιρέτες έχουμε  . Χωρίς λοιπόν βλάβη της γενικότητας έχουμε ότι
. Χωρίς λοιπόν βλάβη της γενικότητας έχουμε ότι  .
. . Επειδή
. Επειδή  αναγκαστικά πρέπει
αναγκαστικά πρέπει  . Πράγματι σε αντίθετη περίπτωση θα είχαμε
. Πράγματι σε αντίθετη περίπτωση θα είχαμε  . Τότε όμως είναι
. Τότε όμως είναι  το οποίο είναι αδύνατον αφού αν
το οποίο είναι αδύνατον αφού αν  , τότε
, τότε  ενώ αν
ενώ αν  τότε
τότε 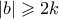 και άρα
και άρα  .
. πύργοι.
πύργοι. .
. :
: .
. (ή μεγαλύτερο) που να μην περιέχει πύργο δεν είναι δυνατό να υπάρξει. Αν υπήρχε, τότε τα τετραγωνάκια του δεν θα ήταν δυνατό να απειλούνται αποκλειστικά από πύργους που θα τοποθετούνταν στις
(ή μεγαλύτερο) που να μην περιέχει πύργο δεν είναι δυνατό να υπάρξει. Αν υπήρχε, τότε τα τετραγωνάκια του δεν θα ήταν δυνατό να απειλούνται αποκλειστικά από πύργους που θα τοποθετούνταν στις 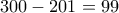 γραμμές (ή λιγότερες για μεγαλύτερο τετράγωνο) που είναι εκτός του τετραγώνου. Θα έπρεπε να στριμωχτούν με κάποιον τρόπο τουλάχιστον
γραμμές (ή λιγότερες για μεγαλύτερο τετράγωνο) που είναι εκτός του τετραγώνου. Θα έπρεπε να στριμωχτούν με κάποιον τρόπο τουλάχιστον  στήλες που είναι εκτός του τετραγώνου. Θα έπρεπε δηλαδή να στριμωχτούν με κάποιον τρόπο τουλάχιστον
στήλες που είναι εκτός του τετραγώνου. Θα έπρεπε δηλαδή να στριμωχτούν με κάποιον τρόπο τουλάχιστον  άρα
άρα  ,
, 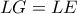 δηλαδή η
δηλαδή η  διχοτομεί την γωνία
διχοτομεί την γωνία  με συνέπεια η
με συνέπεια η 
 .
.  άρα
άρα  ,
,  και η
και η 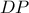 διέρχεται από το κέντρο
διέρχεται από το κέντρο  του εγγεγραμμένου κύκλου στο
του εγγεγραμμένου κύκλου στο  .
.  που ακολουθεί προκύπτει:
που ακολουθεί προκύπτει: 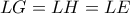 και
και  άρα:
άρα:  και
και .
. και
και  είναι:
είναι: 
 θα είναι
θα είναι  δηλαδή
δηλαδή 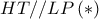 .
.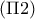 παρακάτω, είναι
παρακάτω, είναι  με συνέπεια η ευθεία
με συνέπεια η ευθεία 
 που διέρχεται από το μέσο
που διέρχεται από το μέσο 
 διέρχεται και από το μέσο
διέρχεται και από το μέσο  .
. δύο χορδές του περιγεγραμμένου του κύκλου από δύο κορυφές του που διέρχονται από το κέντρο
δύο χορδές του περιγεγραμμένου του κύκλου από δύο κορυφές του που διέρχονται από το κέντρο 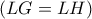 .
. διχοτόμοι, άρα
διχοτόμοι, άρα  και
και  .
.  δηλαδή
δηλαδή  .
.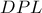 και
και  ο περιγεγραμμένος του κύκλος. Αν
ο περιγεγραμμένος του κύκλος. Αν  το σημείο τομής των εφαπτομένων του
το σημείο τομής των εφαπτομένων του  τότε:
τότε: και η ευθεία της διαμέσου
και η ευθεία της διαμέσου  σχηματίζουν ίσες γωνίες με τις πλευρές του τριγώνου, δηλαδή
σχηματίζουν ίσες γωνίες με τις πλευρές του τριγώνου, δηλαδή  και
και  , όπου
, όπου  το σημείο που η προέκταση της διαμέσου
το σημείο που η προέκταση της διαμέσου  τέμνει τον κύκλο.
τέμνει τον κύκλο.  είναι μεσοκάθετη του
είναι μεσοκάθετη του  των τόξων
των τόξων  .
. προκύπτει:
προκύπτει: 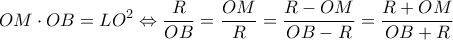 ,
, με συνέπεια
με συνέπεια  εσωτερική και εξωτερική διχοτόμος αντίστοιχα του τριγώνου
εσωτερική και εξωτερική διχοτόμος αντίστοιχα του τριγώνου  .
. είναι μέσο του τόξου
είναι μέσο του τόξου  οπότε
οπότε  και
και