Θέματα της δεύτερης φάσης (τελικής) για την 10η τάξη. Διάρκεια εξέτασης 3 ώρες.
1. Ο Νίκος πολλαπλασίασε όλους τους διαιρέτες ενός φυσικού αριθμού
 . Ο Θοδωρής αύξησε κάθε διαιρέτη κατά 1, και έπειτα πολλαπλασίασε τα αποτελέσματα. Αν το γινόμενο του Θοδωρή διαιρείτε με το γινόμενο του Νίκου, ποιες τιμές μπορεί να πάρει ο
. Ο Θοδωρής αύξησε κάθε διαιρέτη κατά 1, και έπειτα πολλαπλασίασε τα αποτελέσματα. Αν το γινόμενο του Θοδωρή διαιρείτε με το γινόμενο του Νίκου, ποιες τιμές μπορεί να πάρει ο  ;
; 2. Δίνονται οι θετικοί αριθμοί
 , τέτοιοι, ώστε
, τέτοιοι, ώστε 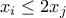 για
για  . Να δείξετε ότι, μπορούν να βρεθούν θετικοί αριθμοί
. Να δείξετε ότι, μπορούν να βρεθούν θετικοί αριθμοί  , τέτοιοι, ώστε
, τέτοιοι, ώστε  για όλα τα
για όλα τα  .
.3. Ο εγγεγραμμένος κύκλος τριγώνου
 εφάπτεται των πλευρών
εφάπτεται των πλευρών  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Στη πλευρά
αντίστοιχα. Στη πλευρά  βρέθηκε σημείο
βρέθηκε σημείο  τέτοιο, ώστε
τέτοιο, ώστε  και
και  . Να δείξετε, ότι
. Να δείξετε, ότι  .
.4. Ο χρωματισμός των κελιών πίνακα
 με άσπρο και μάυρο χρώμα ονομάζεται «επιτρεπτός», αν σε κάθε γραμμή και κάθε στήλη υπάρχουν από 50 έως 60 μαύρα κελιά. Σε έναν επιτρεπτό χρωματισμό επιτρέπεται να αλλάξουμε το χρώμα ενός κελιού αν ο χρωματισμός παραμείνει επιτρεπτός. Να δείξετε ότι με μια τέτοια διαδικασία μπορούμε από οποιαδήποτε επιτρεπτό χρωματισμό να καταλήξουμε σε οποιοδήποτε άλλο επιτρεπτό χρωματισμό.
με άσπρο και μάυρο χρώμα ονομάζεται «επιτρεπτός», αν σε κάθε γραμμή και κάθε στήλη υπάρχουν από 50 έως 60 μαύρα κελιά. Σε έναν επιτρεπτό χρωματισμό επιτρέπεται να αλλάξουμε το χρώμα ενός κελιού αν ο χρωματισμός παραμείνει επιτρεπτός. Να δείξετε ότι με μια τέτοια διαδικασία μπορούμε από οποιαδήποτε επιτρεπτό χρωματισμό να καταλήξουμε σε οποιοδήποτε άλλο επιτρεπτό χρωματισμό. Καταληκτική αίθουσα (*)
5. Έστω
 μια ευθεία και
μια ευθεία και  ,
,  δυο σημεία εκτός αυτής. Θεωρούμε όλα τα δυνατά ορθογώνια τρίγωνα
δυο σημεία εκτός αυτής. Θεωρούμε όλα τα δυνατά ορθογώνια τρίγωνα  με την υποτείνουσά τους επί της
με την υποτείνουσά τους επί της  . Να αποδείξετε ότι, οι περιγεγραμμένοι κύκλοι των τριγώνων
. Να αποδείξετε ότι, οι περιγεγραμμένοι κύκλοι των τριγώνων  , έχουν και ένα άλλο κοινό σημείο εκτός από το
, έχουν και ένα άλλο κοινό σημείο εκτός από το  .
.6. Τεθλασμένη 100 πλευρών, της οποίας καμία τριάδα πλευρών δεν διέρχεται από το ίδιο σημείο, είναι εγγεγραμμένη σε κύκλο. Εξάλλου όλες οι γωνιές της είναι αμβλείες και το άθροισμά τους σε μοίρες διαιρείτε με το 720. Να αποδείξετε, ότι αυτή η τεθλασμένη έχει περιττό αριθμό σημείων τομής με τον εαυτό της.
7. Το πολυώνυμο
 με ακέραιους συντελεστές και ο θετικός ακέραιος
με ακέραιους συντελεστές και ο θετικός ακέραιος  είναι τέτοιοι, ώστε για κάθε ακέραιο
είναι τέτοιοι, ώστε για κάθε ακέραιο  υπάρχει ένας ακέραιος
υπάρχει ένας ακέραιος  για τον οποίο
για τον οποίο 
Nα βρείτε όλα τα ζεύγη
 με την παραπάνω ιδιότητα.
με την παραπάνω ιδιότητα.(*) Όσοι έλυσαν δυο από τα τέσσερα αρχικά προβλήματα καλέστηκαν να λύσουν άλλα τρία σε διαφορετική αίθουσα. Ο επιπλέον χρόνος που δίνεται είναι μια ώρα.
Στατιστικά: Στον πρώτο πίνακα αναγράφεται ο αριθμός των λυτών ανά θέμα (πόσοι έλυσαν το πρώτο, δύτερο θέμα κτλ.). Στον δεύτερο πίνακα ο αριθμός των μαθητών ανά πλήθος θεμάτων που έλυσαν(πόσοι έλυσαν ένα, δυο κτλ θέματα).



 . Tότε πρέπει
. Tότε πρέπει  ,όπου
,όπου  ,
,  . Διακρίνουμε
. Διακρίνουμε  περιπτώσεις:
περιπτώσεις:  Υποθέτουμε ότι ο
Υποθέτουμε ότι ο 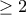 διαιρέτες (δηλαδή είναι διάφορος του
διαιρέτες (δηλαδή είναι διάφορος του  ) Συνεπώς όλοι οι διαρέτες του
) Συνεπώς όλοι οι διαρέτες του  άρτιοι. Πρέπει
άρτιοι. Πρέπει  . Και αφού
. Και αφού  πρέπει
πρέπει  . Όμως για κάθε
. Όμως για κάθε  ισχύει
ισχύει  , συνεπώς θα ισχύει
, συνεπώς θα ισχύει  , άτοπο. Άρα η μόνη λύση εδώ είναι
, άτοπο. Άρα η μόνη λύση εδώ είναι  , που ικανοποιεί.
, που ικανοποιεί. Υποθέτουμε ότι ο
Υποθέτουμε ότι ο  διαιρέτες (δηλαδή είναι διάφορος του
διαιρέτες (δηλαδή είναι διάφορος του  ). Προφανώς είναι
). Προφανώς είναι  . Έχουμε
. Έχουμε  και
και  . Πρέπει λοιπόν
. Πρέπει λοιπόν  . Είναι όμως
. Είναι όμως  και επομένως
και επομένως  . Άρα πρέπει
. Άρα πρέπει  . Θα δείξουμε επαγωγικά ότι
. Θα δείξουμε επαγωγικά ότι  . Έστω για ένα
. Έστω για ένα 
 . Θα δείξουμε ότι ισχύει και για
. Θα δείξουμε ότι ισχύει και για  . Πρέπει να δείξουμε ότι
. Πρέπει να δείξουμε ότι  . Είναι προφανές πως
. Είναι προφανές πως  (αφού ο
(αφού ο  αποτελεί τον δεύτερο μεγαλύτερο διαιρέτη του
αποτελεί τον δεύτερο μεγαλύτερο διαιρέτη του  (μετά από τον ίδιο) και άρα θα ισχύει
(μετά από τον ίδιο) και άρα θα ισχύει 

 , αυτό που θέλαμε). Έτσι με πολλαπλασιασμό με την
, αυτό που θέλαμε). Έτσι με πολλαπλασιασμό με την 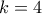 . Θα δείξουμε ότι
. Θα δείξουμε ότι  , που είναι προφανές αφού
, που είναι προφανές αφού  και
και  για τον λόγο που δείξαμε παραπάνω. Συνεπώς, αφού ισχύει ότι για
για τον λόγο που δείξαμε παραπάνω. Συνεπώς, αφού ισχύει ότι για  και άρα
και άρα  θα ισχύει για κάθε
θα ισχύει για κάθε  . Συνεπώς, ελέγχοντας τις περιπτώσεις
. Συνεπώς, ελέγχοντας τις περιπτώσεις  παίρνουμε
παίρνουμε  .
. το ύψος του τριγώνου
το ύψος του τριγώνου  ως προς τον κύκλο
ως προς τον κύκλο  .
. επανατέμνει τον κύκλο στο
επανατέμνει τον κύκλο στο  , τότε το
, τότε το 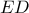 είναι σταθερό, αφού,
είναι σταθερό, αφού,  . Άρα όλοι οι κύκλοι διέρχονται και από το
. Άρα όλοι οι κύκλοι διέρχονται και από το 
 .
. τότε
τότε  , διαφορετικά το
, διαφορετικά το  . Άρα σε κάθε περίπτωση είναι
. Άρα σε κάθε περίπτωση είναι  .
. , είναι
, είναι 