Θέματα της δεύτερης φάσης (τελικής) για την 8η τάξη. Διάρκεια εξέτασης 3 ώρες. (*)[/i][/b]
[b]1.[/b] Οι ακέραιοι μη μηδενικοί αριθμοί
 είναι τέτοιοι, ώστε
είναι τέτοιοι, ώστε  . Επιπλέον αυτά τα τέσσερα κλάσματα είναι ανάγωγα, δεν είναι ακέραιοι αριθμοί και δεν είναι απαραίτητα θετικά. Να βρείτε το
. Επιπλέον αυτά τα τέσσερα κλάσματα είναι ανάγωγα, δεν είναι ακέραιοι αριθμοί και δεν είναι απαραίτητα θετικά. Να βρείτε το  .
.[b]2.[/b] Σε τραπέζιο
 το σημείο
το σημείο  είναι το μέσο της πλάγιας πλευράς του
είναι το μέσο της πλάγιας πλευράς του  και το σημείο
και το σημείο  είναι το ίχνος της καθέτου από το
είναι το ίχνος της καθέτου από το  προς την άλλη πλάγια πλευρά
προς την άλλη πλάγια πλευρά  . Αν
. Αν  να αποδείξετε, ότι
να αποδείξετε, ότι  .
.[b]3.[/b] Ο σκακιστικός πεσσός «καγκουρό» απειλεί 8 τετράγωνα τα οποία είναι δυο ή τρία τετράγωνα αριστερά, δεξιά, πάνω ή κάτω από την παρούσα θέση του (δεν απειλεί τα γειτονικά τετράγωνα). Ποιος είναι ο μεγαλύτερος αριθμός καγκουρό που μπορούμε να τοποθετήσουμε σε μια
 σκακιέρα ώστε να μην απειλούνται μεταξύ τους;
σκακιέρα ώστε να μην απειλούνται μεταξύ τους;[b]4.[/b] Δίνονται 30 διαφορετικοί θετικοί φυσικοί αριθμοί για κάθε έναν από τους οποίους το προτελευταίο ψηφίο είναι μεγαλύτερο του 5. Για όλους αυτούς τους αριθμούς εκτελούμε την Ευκλείδεια διαίρεση με διαιρέτη το 99 και τα πηλίκα και υπόλοιπα που προκύπτουν τα καταγράφουμε στο πίνακα. Να αποδείξετε ότι ανάμεσα στους 60 καταγραμμένους αριθμούς τουλάχιστον 9 είναι διαφορετικοί.
[b]Καταληκτική αίθουσα (**)[/b]
[b]5.[/b] Δίνονται οι θετικοί αριθμοί
 . Προέκυψε ότι ο
. Προέκυψε ότι ο  είναι πέντε φορές μεγαλύτερος από τον μέσο όρο όλων των αριθμών. Ποια είναι ελάχιστη τιμή που μπορεί να έχει ο
είναι πέντε φορές μεγαλύτερος από τον μέσο όρο όλων των αριθμών. Ποια είναι ελάχιστη τιμή που μπορεί να έχει ο  ;
;[b]6.[/b] Σε τρίγωνο
 με
με  φέρουμε την διχοτόμο
φέρουμε την διχοτόμο 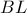 . Στην πλευρά
. Στην πλευρά  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο, ώστε
τέτοιο, ώστε  . Οι ευθείες
. Οι ευθείες  και
και 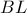 τέμνονται στο σημείο
τέμνονται στο σημείο  . Να αποδείξετε, ότι τα εμβαδά των τριγώνων
. Να αποδείξετε, ότι τα εμβαδά των τριγώνων  και
και  είναι ίσα.
είναι ίσα.[b]7.[/b] Κάθε μέλος του συλλόγου εύθυμης αχρωματοψίας γνωρίζεται το πολύ με άλλα δέκα μέλη. Ο σύλλογος αγόρασε γάντια 23 διαφορετικών χρωμάτων (γάντια του ίδιου χρώματος είναι απεριόριστα). Στην πρωτοχρονιάτικη δεξίωση του συλλόγου τα μέλη προσέρχονταν ο ένας μετά τον άλλον και ο καθένας, με την είσοδό του, έβρισκε, ότι τα μέλη με τα οποία γνωρίζεται και ήδη έχουν προσέλθει, γνωρίζονται και μεταξύ τους. Να αποδείξετε, ότι μετά την αλλαγή του χρόνου (που δίνονται τα δώρα) σε κάθε μέλος του συλλόγου μπορούμε να δωρίσουμε γάντια διαφορετικού χρώματος έτσι, ώστε δυο οποιαδήποτε μέλη που γνωρίζονται μεταξύ τους να έχουν γάντια τεσσάρων διαφορετικών χρωμάτων και οποιαδήποτε δυο μέλη που έχουν κοινό γνωστό, γάντια τουλάχιστον τριών διαφορετικών χρωμάτων.
[size=85][i](*) Η τελική φάση της ολυμπιάδας είναι προφορική.
(**) Όσοι έλυσαν δυο από τα τέσσερα αρχικά προβλήματα καλέστηκαν να λύσουν άλλα τρία σε διαφορετική αίθουσα. Ο επιπλέον χρόνος που δίνεται είναι μια ώρα.[/i]
Στατιστικά: Στον πρώτο πίνακα αναγράφεται ο αριθμός των λυτών ανά θέμα (πόσοι έλυσαν το πρώτο, δύτερο θέμα κτλ.). Στον δεύτερο πίνακα ο αριθμός των μαθητών ανά πλήθος θεμάτων που έλυσαν(πόσοι έλυσαν ένα, δυο κτλ θέματα).

 [/size]
[/size]
 μέσο του
μέσο του 


 . Η αρχική γίνεται:
. Η αρχική γίνεται:  . Πρέπει λοιπόν
. Πρέπει λοιπόν 

 . Ομoίως παίρνουμε:
. Ομoίως παίρνουμε:  ,
,  ,
,  . Συνεπώς,
. Συνεπώς, 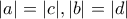 . Αν
. Αν  , η αρχική γίνεται:
, η αρχική γίνεται: 
 , αν
, αν  , έχουμε άτοπο. Συνεπώς,
, έχουμε άτοπο. Συνεπώς,  , αντικαθιστούμε και παίρνουμε:
, αντικαθιστούμε και παίρνουμε: , που ισχύει. Συνεπώς, σε αυτήν την περίπτωση
, που ισχύει. Συνεπώς, σε αυτήν την περίπτωση  . Ομοίως και στην άλλη.
. Ομοίως και στην άλλη. οπότε τα τρίγωνα
οπότε τα τρίγωνα 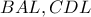 είναι ίσα (Π-Γ-Π), άρα
είναι ίσα (Π-Γ-Π), άρα 
 Τα τρίγωνα
Τα τρίγωνα 
 , επειδή τα τρίγωνα
, επειδή τα τρίγωνα  είναι όμοια.
είναι όμοια. και
και 
 ο μέσος όρος όλων των αριθμών, τότε
ο μέσος όρος όλων των αριθμών, τότε  .
.
 λόγω της
λόγω της  γίνεται:
γίνεται: 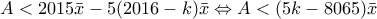 .
. οπότε
οπότε  , δηλαδή η ελάχιστη τιμή του
, δηλαδή η ελάχιστη τιμή του  .
. .
. . Αλέξανδρε, μπορείς να μας διαφωτίσεις;
. Αλέξανδρε, μπορείς να μας διαφωτίσεις;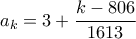 για
για  ,
, 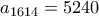 και
και 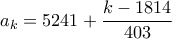 για
για 
 τότε ο αριθμός θα ήταν ο
τότε ο αριθμός θα ήταν ο  , άτοπο αφού το προτελευταίο ψηφίο του ισούται με
, άτοπο αφού το προτελευταίο ψηφίο του ισούται με  .
.  ισούνται με
ισούνται με  και
και  για κάποια
για κάποια  . Τότε όμως
. Τότε όμως  . Αυτό όμως είναι αδύνατο αφού αν τα προτελευταία ψηφία των
. Αυτό όμως είναι αδύνατο αφού αν τα προτελευταία ψηφία των  δεν μπορεί να είναι πολλαπλάσιο του
δεν μπορεί να είναι πολλαπλάσιο του  .
. το σύνολο όλων των πηλίκων και υπολοίπων που καταγράψαμε και έστω
το σύνολο όλων των πηλίκων και υπολοίπων που καταγράψαμε και έστω 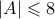 . Τότε το
. Τότε το 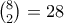 υποσύνολα δύο στοιχείων. Από τα πιο πάνω όμως, κάθε ένας από τους
υποσύνολα δύο στοιχείων. Από τα πιο πάνω όμως, κάθε ένας από τους  αριθμούς που ξεκινήσαμε αντιστοιχεί σε διαφορετικό υποσύνολο δύο στοιχείων. Αυτό είναι άτοπο.
αριθμούς που ξεκινήσαμε αντιστοιχεί σε διαφορετικό υποσύνολο δύο στοιχείων. Αυτό είναι άτοπο.
 . Αλλά ήδη απορρίψαμε την περίπτωση
. Αλλά ήδη απορρίψαμε την περίπτωση  στην πρώτη παράγραφο.
στην πρώτη παράγραφο. και
και  .
.

 .
. .
. άτομα τα οποία ήδη έχουν προσέλθει.
άτομα τα οποία ήδη έχουν προσέλθει. χρώματα στην διάθεσή μας ώστε με κάθε γνωστό του να έχουν γάντια τεσσάρων διαφορετικών χρωμάτων. Έχουμε λοιπόν
χρώματα στην διάθεσή μας ώστε με κάθε γνωστό του να έχουν γάντια τεσσάρων διαφορετικών χρωμάτων. Έχουμε λοιπόν  δυνατές επιλογές. Από αυτές πρέπει να απορρίψουμε τις επιλογές όπου μαζί με ένα άλλο μέλος που έχει ήδη προσέλθει και που έχουν κοινό γνωστό δώσαμε γάντια μόνο δύο χρωμάτων. Συνολικά όμως υπάρχουν το πολύ
δυνατές επιλογές. Από αυτές πρέπει να απορρίψουμε τις επιλογές όπου μαζί με ένα άλλο μέλος που έχει ήδη προσέλθει και που έχουν κοινό γνωστό δώσαμε γάντια μόνο δύο χρωμάτων. Συνολικά όμως υπάρχουν το πολύ  τέτοια μέλη. Αν λοιπόν δειχθεί ότι
τέτοια μέλη. Αν λοιπόν δειχθεί ότι  τότε τελειώσαμε.
τότε τελειώσαμε. 
 το πολύ καγκουρό και μένουν κενά τα
το πολύ καγκουρό και μένουν κενά τα  κεντρικά κελιά .
κεντρικά κελιά . 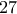 καγκουρό που είναι και ο μέγιστος αριθμός (σχήμα 4).
καγκουρό που είναι και ο μέγιστος αριθμός (σχήμα 4). και
και  ορθογώνια που περιτριγυρίζουν το κεντρικό
ορθογώνια που περιτριγυρίζουν το κεντρικό  τετράγωνο πρέπει να έχουν από ένα καγκουρό το καθένα. Υπάρχει μοναδικός τρόπος να τοποθετηθούν. Το επόμενο βήμα είναι να παρατηρήσουμε ότι οι πεντάδες του σχήματος 2 αλλά και οι συμμετρικές τους πρέπει να έχουν από 2 καγκουρό όπως στο σχήμα 1. Πλέον ένα ένα τα καγκουρό καθορίζονται στο που πρέπει να βρίσκονται.
τετράγωνο πρέπει να έχουν από ένα καγκουρό το καθένα. Υπάρχει μοναδικός τρόπος να τοποθετηθούν. Το επόμενο βήμα είναι να παρατηρήσουμε ότι οι πεντάδες του σχήματος 2 αλλά και οι συμμετρικές τους πρέπει να έχουν από 2 καγκουρό όπως στο σχήμα 1. Πλέον ένα ένα τα καγκουρό καθορίζονται στο που πρέπει να βρίσκονται.