Demetres έγραψε: ↑Τρί Απρ 18, 2017 8:32 pm
Άσκηση 14: Όταν το

διαιρεθεί με τους

και

, αφήνει υπόλοιπα

και

. Να βρεθεί ο ελάχιστος αριθμός με την ίδια ιδιότητα ο οποίος μπορεί να σχηματιστεί χρησιμοποιώντας τα ψηφία

το πολύ μία φορά το κάθε ένα.
Βάζω μια διαφορετική λύση.
Επειδή ο αριθμός αφήνει υπόλοιπο

όταν διαιρεθεί με το

, πρέπει να λήγει σε

ή

.
Επειδή ο αριθμός είναι πολλαπλάσιο του

, πρέπει το άθροισμα τον ψηφίων του να είναι πολλαπλάσιο του

.
Το άλλο κριτήριο που θα χρησιμοποιήσουμε λέει το εξής: Το υπόλοιπο της διαίρεσης του αριθμού

όταν διαιρεθεί με το

ισούται με το υπόλοιπο της διαίρεσης του

με το

.
Π.χ. το υπόλοιπο της διαίρεσης του

με το

ισούται με το υπόλοιπο της διαίρεσης του
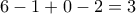
με το

.
Πρέπει λοιπόν, προσθαφαιρώντας τους

να καταλήξουμε σε κάποιον από τους αριθμούς

ή ακόμη και τους

. Τα

καθώς και τα

είναι αδύνατον να εμφανιστούν αφού οι αριθμοί είναι πολύ μικροί.
Το

εμφανίζεται μόνο ως

ή

.
Το

εμφανίζεται μόνο ως

.
To

απορρίπτεται επειδή το άθροισμα των ψηφίων θα ισούται με

που δεν είναι πολλαπλάσιο του

.
Άρα:
Είτε θα χρησιμοποιήσουμε τους

και

στις περιττές θέσεις και ίσως τον

οπουδήποτε.
Είτε θα χρησιμοποιήσουμε τον

σε περιττή θέση, τους

και

σε άρτια θέση, και ίσως τον

οπουδήποτε.
Λαμβάνοντας υπόψη και τις άλλες συνθήκες οι μόνοι αριθμοί που ικανοποιούν όλες τις διαιρετότητες είναι οι
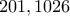
και

.
Μικρότερος όλων είναι ο

.
διαιρεθεί με τους
και
, αφήνει υπόλοιπα
και
. Να βρεθεί ο ελάχιστους αριθμός με την ίδια ιδιότητα ο οποίος μπορεί να σχηματιστεί χρησιμοποιόντας τα ψηφία
το πολύ μία φορά το κάθε ένα.
ο αριθμός . Άρα , από εκφώνηση έχω :
.
. Προφανής λύση
.
.
.
και βρίσκουμε ότι ο ελάχιστος αριθμός είναι





 μια γραμμική διοφαντική εξίωση και
μια γραμμική διοφαντική εξίωση και  ο ΜΚΔ των
ο ΜΚΔ των  . Τότε :
. Τότε : Η εξίσωση (1) έχει λύση , αν και μόνο αν ο
Η εξίσωση (1) έχει λύση , αν και μόνο αν ο  .
. , η εξίσωση (1) έχει άπειρες λύσεις , που δίνονται από τους τύπους :
, η εξίσωση (1) έχει άπειρες λύσεις , που δίνονται από τους τύπους :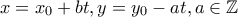 όπου
όπου  μια λύση της (1) .
μια λύση της (1) . όταν διαιρεθεί με το
όταν διαιρεθεί με το  , πρέπει να λήγει σε
, πρέπει να λήγει σε  .
. όταν διαιρεθεί με το
όταν διαιρεθεί με το  με το
με το 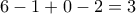 με το
με το  να καταλήξουμε σε κάποιον από τους αριθμούς
να καταλήξουμε σε κάποιον από τους αριθμούς  ή ακόμη και τους
ή ακόμη και τους  . Τα
. Τα  καθώς και τα
καθώς και τα  είναι αδύνατον να εμφανιστούν αφού οι αριθμοί είναι πολύ μικροί.
είναι αδύνατον να εμφανιστούν αφού οι αριθμοί είναι πολύ μικροί.  ή
ή  .
. εμφανίζεται μόνο ως
εμφανίζεται μόνο ως  .
. που δεν είναι πολλαπλάσιο του
που δεν είναι πολλαπλάσιο του  στις περιττές θέσεις και ίσως τον
στις περιττές θέσεις και ίσως τον  οπουδήποτε.
οπουδήποτε.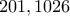 και
και  .
.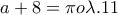





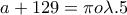

 είναι ένα Κοινό Πολλαπλάσιο των
είναι ένα Κοινό Πολλαπλάσιο των 
 είναι το
είναι το 
 οπότε
οπότε 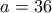 που απορρίπτεται.
που απορρίπτεται.  οπότε
οπότε  που είναι ο ζητούμενος αριθμός.
που είναι ο ζητούμενος αριθμός.