BMO 2017 - Θέματα
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
BMO 2017 - Θέματα
Σήμερα είναι η ημέρα του διαγωνισμού! Καλή επιτυχία στους μαθητές Ελλάδας και Κύπρου!
Τα θέματα θα ανέβουν αμέσως μετά τη λήξη του διαγωνισμού και θα τα συζητήσουμε εδώ!
Πρώτα στοιχεία είναι ότι το Πρόβλημα 1 είναι της Μολδαβίας, το δεύτερο της Ελλάδας, το τρίτο της Αλβανίας και το 4 της Κύπρου και έτσι συνεχίζεται η παράδοση της επιλογής προβλημάτων που έστειλαν οι δύο χώρες!! Συγχαρητήρια στους δημιουργούς!
Για περισσότερα θα μας ενημερώσουν οι φίλοι που συνοδεύουν τους μαθητές μας!
Αλέξανδρος
Τα θέματα θα ανέβουν αμέσως μετά τη λήξη του διαγωνισμού και θα τα συζητήσουμε εδώ!
Πρώτα στοιχεία είναι ότι το Πρόβλημα 1 είναι της Μολδαβίας, το δεύτερο της Ελλάδας, το τρίτο της Αλβανίας και το 4 της Κύπρου και έτσι συνεχίζεται η παράδοση της επιλογής προβλημάτων που έστειλαν οι δύο χώρες!! Συγχαρητήρια στους δημιουργούς!
Για περισσότερα θα μας ενημερώσουν οι φίλοι που συνοδεύουν τους μαθητές μας!
Αλέξανδρος
Αλέξανδρος Συγκελάκης
Λέξεις Κλειδιά:
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: BMO 2017 - Θέματα
Μια και ο διαγωνισμός έχει ήδη τελειώσει επισυνάπτω τα θέματα. Τα συγχαρητήρια μου στον Βαγγέλη Ψύχα και Σιλουανό Μπραζιτίκο για το δεύτερο θέμα του διαγωνισμού και στον Δημήτρη Χριστοφίδη για το τέταρτο θέμα.
Αλέξανδρος
Αλέξανδρος
- Συνημμένα
-
- BMO_2017_Greek_Version.pdf
- (42.2 KiB) Μεταφορτώθηκε 464 φορές
Αλέξανδρος Συγκελάκης
Re: BMO 2017 - Θέματα
Πρόβλημα 1
Να βρείτε όλα τα διατεταγμένα ζεύγη θετικών ακεραίων , τέτοια ώστε:
, τέτοια ώστε: 
(Μολδαβία)
Πρόβλημα 2
Έστω οξυγώνιο τρίγωνο με
οξυγώνιο τρίγωνο με  και έστω
και έστω  ο περιγεγραμμένος κύκλος του. Έστω
ο περιγεγραμμένος κύκλος του. Έστω  και
και  οι εφαπτομένες του κύκλου
οι εφαπτομένες του κύκλου  στα σημεία
στα σημεία  και
και  , αντίστοιχα, και έστω
, αντίστοιχα, και έστω  το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο
το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο  και είναι παράλληλη προς την
και είναι παράλληλη προς την  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Η ευθεία που διέρχεται από το σημείο
. Η ευθεία που διέρχεται από το σημείο  και είναι παράλληλη προς την
και είναι παράλληλη προς την  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Ο περιγεγραμμένος κύκλος στο τρίγωνο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο  τέμνει την πλευρά
τέμνει την πλευρά  σε σημείο
σε σημείο  , με το
, με το  να βρίσκεται ανάμεσα στα
να βρίσκεται ανάμεσα στα  και
και  . Ο περιγεγραμμένος κύκλος στο τρίγωνο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο  τέμνει την ευθεία
τέμνει την ευθεία  σε σημείο
σε σημείο  , με το
, με το  να βρίσκεται ανάμεσα στα
να βρίσκεται ανάμεσα στα  και
και  .
.
Να αποδείξετε ότι οι ευθείες και
και  συντρέχουν.
συντρέχουν.
(Ελλάδα)
Πρόβλημα 3
Έστω το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις
το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις  , για τις οποίες ο
, για τις οποίες ο  διαιρεί τον
διαιρεί τον  , για όλα τα
, για όλα τα  .
.
(Αλβανία)
Πρόβλημα 4
Σε ένα κυκλικό τραπέζι κάθονται μαθητές. Αρχικά, κάθε μαθητής έχει ακριβώς μία καραμέλα. Σε κάθε βήμα, κάθε μαθητής επιλέγει μία από τις ακόλουθες ενέργειες:
μαθητές. Αρχικά, κάθε μαθητής έχει ακριβώς μία καραμέλα. Σε κάθε βήμα, κάθε μαθητής επιλέγει μία από τις ακόλουθες ενέργειες:
(α) Δίνει μία καραμέλα στον μαθητή που κάθεται στα αριστερά του ή στον μαθητή που κάθεται στα δεξιά του.
(β) Χωρίζει όλες τις καραμέλες του σε δύο, πιθανώς κενά, σύνολα και δίνει το ένα σύνολο στον μαθητή που κάθεται στα αριστερά του και το άλλο στον μαθητή που κάθεται στα δεξιά του.
Σε κάθε βήμα, οι μαθητές εκτελούν τις ενέργειες που έχουν επιλέξει ταυτόχρονα.
Μία κατανομή των καραμελών ονομάζεται νόμιμη, αν μπορεί να προκύψει μετά από πεπερασμένο πλήθος βημάτων.
Να βρείτε το πλήθος των νόμιμων κατανομών.
(Δύο κατανομές είναι διαφορετικές αν υπάρχει μαθητής ο οποίος να έχει διαφορετικό αριθμό καραμελών σε κάθε μία από τις κατανομές αυτές.)
(Κύπρος)
Να βρείτε όλα τα διατεταγμένα ζεύγη θετικών ακεραίων
 , τέτοια ώστε:
, τέτοια ώστε: 
(Μολδαβία)
Πρόβλημα 2
Έστω
 οξυγώνιο τρίγωνο με
οξυγώνιο τρίγωνο με  και έστω
και έστω  ο περιγεγραμμένος κύκλος του. Έστω
ο περιγεγραμμένος κύκλος του. Έστω  και
και  οι εφαπτομένες του κύκλου
οι εφαπτομένες του κύκλου  στα σημεία
στα σημεία  και
και  , αντίστοιχα, και έστω
, αντίστοιχα, και έστω  το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο
το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο  και είναι παράλληλη προς την
και είναι παράλληλη προς την  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Η ευθεία που διέρχεται από το σημείο
. Η ευθεία που διέρχεται από το σημείο  και είναι παράλληλη προς την
και είναι παράλληλη προς την  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Ο περιγεγραμμένος κύκλος στο τρίγωνο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο  τέμνει την πλευρά
τέμνει την πλευρά  σε σημείο
σε σημείο  , με το
, με το  να βρίσκεται ανάμεσα στα
να βρίσκεται ανάμεσα στα  και
και  . Ο περιγεγραμμένος κύκλος στο τρίγωνο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο  τέμνει την ευθεία
τέμνει την ευθεία  σε σημείο
σε σημείο  , με το
, με το  να βρίσκεται ανάμεσα στα
να βρίσκεται ανάμεσα στα  και
και  .
.Να αποδείξετε ότι οι ευθείες
 και
και  συντρέχουν.
συντρέχουν.(Ελλάδα)
Πρόβλημα 3
Έστω
 το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις
το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις  , για τις οποίες ο
, για τις οποίες ο  διαιρεί τον
διαιρεί τον  , για όλα τα
, για όλα τα  .
.(Αλβανία)
Πρόβλημα 4
Σε ένα κυκλικό τραπέζι κάθονται
 μαθητές. Αρχικά, κάθε μαθητής έχει ακριβώς μία καραμέλα. Σε κάθε βήμα, κάθε μαθητής επιλέγει μία από τις ακόλουθες ενέργειες:
μαθητές. Αρχικά, κάθε μαθητής έχει ακριβώς μία καραμέλα. Σε κάθε βήμα, κάθε μαθητής επιλέγει μία από τις ακόλουθες ενέργειες:(α) Δίνει μία καραμέλα στον μαθητή που κάθεται στα αριστερά του ή στον μαθητή που κάθεται στα δεξιά του.
(β) Χωρίζει όλες τις καραμέλες του σε δύο, πιθανώς κενά, σύνολα και δίνει το ένα σύνολο στον μαθητή που κάθεται στα αριστερά του και το άλλο στον μαθητή που κάθεται στα δεξιά του.
Σε κάθε βήμα, οι μαθητές εκτελούν τις ενέργειες που έχουν επιλέξει ταυτόχρονα.
Μία κατανομή των καραμελών ονομάζεται νόμιμη, αν μπορεί να προκύψει μετά από πεπερασμένο πλήθος βημάτων.
Να βρείτε το πλήθος των νόμιμων κατανομών.
(Δύο κατανομές είναι διαφορετικές αν υπάρχει μαθητής ο οποίος να έχει διαφορετικό αριθμό καραμελών σε κάθε μία από τις κατανομές αυτές.)
(Κύπρος)
Σωτήρης Λοϊζιάς
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: BMO 2017 - Θέματα
Πρόβλημα 1
Η εξίσωση αλλιώς γράφεται:

Οπότε ο είναι ακέραιος.
είναι ακέραιος.
Άρα θα είναι και ο .
.
Έστω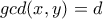 . Τότε
. Τότε  και
και  με
με  .
.
Η παραπάνω γράφεται: ακέραιος.
ακέραιος.
Όμως
Άρα ο είναι ακέραιος διακρίνοντας τις περιπτώσεις:
είναι ακέραιος διακρίνοντας τις περιπτώσεις:
1) η οποία δίνει
η οποία δίνει  Οπότε θα έχουμε
Οπότε θα έχουμε  από όπου προκύπτει η λύση
από όπου προκύπτει η λύση

2) το οποίο τριώνυμο έχει διακρίνουσα
το οποίο τριώνυμο έχει διακρίνουσα  Η οποία
Η οποία
Πρέπει να είναι τέλειο τετράγωνο. Με έλεγχο προκύπτουν οι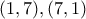
Edit: Απροσεξϊα
Η εξίσωση αλλιώς γράφεται:

Οπότε ο
 είναι ακέραιος.
είναι ακέραιος.Άρα θα είναι και ο
 .
.Έστω
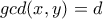 . Τότε
. Τότε  και
και  με
με  .
.Η παραπάνω γράφεται:
 ακέραιος.
ακέραιος.Όμως

Άρα ο
 είναι ακέραιος διακρίνοντας τις περιπτώσεις:
είναι ακέραιος διακρίνοντας τις περιπτώσεις:1)
 η οποία δίνει
η οποία δίνει  Οπότε θα έχουμε
Οπότε θα έχουμε  από όπου προκύπτει η λύση
από όπου προκύπτει η λύση
2)
 το οποίο τριώνυμο έχει διακρίνουσα
το οποίο τριώνυμο έχει διακρίνουσα  Η οποία
Η οποίαΠρέπει να είναι τέλειο τετράγωνο. Με έλεγχο προκύπτουν οι
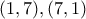
Edit: Απροσεξϊα
τελευταία επεξεργασία από Γιάννης Μπόρμπας σε Πέμ Μάιος 04, 2017 5:15 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Γιάννης Μπορμπαντωνάκης
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: BMO 2017 - Θέματα
Καλή επιτυχία στις ομάδες μας!Soteris έγραψε:Πρόβλημα 1
Να βρείτε όλα τα διατεταγμένα ζεύγη θετικών ακεραίων, τέτοια ώστε:
(Μολδαβία)
Έστω
 , και
, και  με
με  , και η εξίσωση γίνεται (μετά από πράξεις)
, και η εξίσωση γίνεται (μετά από πράξεις) 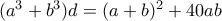 .
.Αυτή γράφεται
 , οπότε,
, οπότε,  , και αφού
, και αφού  (εύκολο),
(εύκολο),  .
.Άρα,
 , ή
, ή  .
.Αν
 ,
,  , άρα
, άρα  , και με αντικατάσταση στην αρχική,
, και με αντικατάσταση στην αρχική,  .
.Αν
 ,
,  ή
ή  , οπότε
, οπότε  .
.Τελικά , λύσεις
 .
. Κερδίζουμε ό,τι τολμούμε!
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: BMO 2017 - Θέματα
Soteris έγραψε:Πρόβλημα 3
Έστωτο σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις
, για τις οποίες ο
διαιρεί τον
, για όλα τα
.
(Αλβανία)
Για
 εύκολα έχουμε
εύκολα έχουμε 
Για
 έπεται ότι
έπεται ότι  οπότε
οπότε  για κάθε
για κάθε 
Οπότε η αρχική συνθήκη γράφεται

Είναι
 οπότε
οπότε  ή
ή 
-- Αν
 τότε, για
τότε, για  έπεται ότι
έπεται ότι  οπότε
οπότε  για κάθε
για κάθε  που είναι λύση.
που είναι λύση.-- Αν
 θα δείξουμε ότι
θα δείξουμε ότι  για κάθε
για κάθε  (που είναι λύση).
(που είναι λύση).Αν υπάρχει
 ώστε
ώστε  τότε από
τότε από  έπεται ότι η
έπεται ότι η  είναι άνω φραγμένη.
είναι άνω φραγμένη.Από
 για
για  στην
στην  και
και από
 για
για  στην
στην 
έχουμε ότι
 για κάθε
για κάθε 
Επειδή
 έπεται ότι
έπεται ότι  για κάθε
για κάθε 
Επομένως, η
 δεν είναι άνω φραγμένη, άτοπο.
δεν είναι άνω φραγμένη, άτοπο.Θανάσης Κοντογεώργης
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: BMO 2017 - Θέματα
Προβλημα 3
Η αρχική σχέση γίνεται:
Προφανή λύση: .
.
Έστω ότι υπάρχει τέτοιος ώστε
τέτοιος ώστε  .
.
Η συνάρτηση πρέπει να είναι άνω και κάτω φραγμένη. Διαφορετικά για αρκετά μεγάλα
 ο παρονομαστής γίνεται μεγαλύτερος από τον αριθμητή. Παίρνοντας
ο παρονομαστής γίνεται μεγαλύτερος από τον αριθμητή. Παίρνοντας 
έχουμε . Ενώ για
. Ενώ για  στην δοθείσα:
στην δοθείσα:  ή αλλιώς
ή αλλιώς
 . Ο αριθμητής είναι άνω φραγμένος. Έστω
. Ο αριθμητής είναι άνω φραγμένος. Έστω  η μέγιστη τιμή της
η μέγιστη τιμή της  . Άρα
. Άρα  αν
αν 
Παίρνοντας έχουμε
έχουμε  άτοπο άρα προκύπτει η λύση
άτοπο άρα προκύπτει η λύση
 .
.
Edit: Ασάφεια.
Η αρχική σχέση γίνεται:

Προφανή λύση:
 .
.Έστω ότι υπάρχει
 τέτοιος ώστε
τέτοιος ώστε  .
.Η συνάρτηση πρέπει να είναι άνω και κάτω φραγμένη. Διαφορετικά για αρκετά μεγάλα
 ο παρονομαστής γίνεται μεγαλύτερος από τον αριθμητή. Παίρνοντας
ο παρονομαστής γίνεται μεγαλύτερος από τον αριθμητή. Παίρνοντας 
έχουμε
 . Ενώ για
. Ενώ για  στην δοθείσα:
στην δοθείσα:  ή αλλιώς
ή αλλιώς . Ο αριθμητής είναι άνω φραγμένος. Έστω
. Ο αριθμητής είναι άνω φραγμένος. Έστω  η μέγιστη τιμή της
η μέγιστη τιμή της  . Άρα
. Άρα  αν
αν 
Παίρνοντας
 έχουμε
έχουμε  άτοπο άρα προκύπτει η λύση
άτοπο άρα προκύπτει η λύση .
.Edit: Ασάφεια.
τελευταία επεξεργασία από Γιάννης Μπόρμπας σε Πέμ Μάιος 04, 2017 6:13 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Γιάννης Μπορμπαντωνάκης
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: BMO 2017 - Θέματα
Θα αποδείξουμε πως οι περιγεγραμμένοι κύκλοι τωνSoteris έγραψε:
Πρόβλημα 2
Έστωοξυγώνιο τρίγωνο με
και έστω
ο περιγεγραμμένος κύκλος του. Έστω
και
οι εφαπτομένες του κύκλου
στα σημεία
και
, αντίστοιχα, και έστω
το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την πλευρά
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την ευθεία
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
.
Να αποδείξετε ότι οι ευθείεςκαι
συντρέχουν.
(Ελλάδα)
 και
και  εφάπτονται των
εφάπτονται των  και
και  αντίστοιχα.
αντίστοιχα.Για τον πρώτο, αρκεί να δείξουμε πως
 .
.Με άλλα λόγια αρκεί:

 , που ισχύει.
, που ισχύει.Ομοίως δουλεύουμε για τον δεύτερο.
Πράγματι λοιπόν οι περιγεγραμμένοι κύκλοι των
 και
και  εφάπτονται των
εφάπτονται των  και
και  αντίστοιχα.
αντίστοιχα.Ακόμη η
 είναι αντιπαράλληλη της
είναι αντιπαράλληλη της  στο τρίγωνο
στο τρίγωνο  (έχουμε το εκφυλισμένο εγγράψιμο
(έχουμε το εκφυλισμένο εγγράψιμο  ). Άρα η συμμετροδιάμεσος της κορυφής
). Άρα η συμμετροδιάμεσος της κορυφής  , δηλαδή η
, δηλαδή η  περνάει από το μέσο του
περνάει από το μέσο του  , έστω
, έστω  . Όμοια η
. Όμοια η  περνάει και από το μέσο
περνάει και από το μέσο  της
της  .
.Από τη δέσμη
 , επειδή η
, επειδή η  διχοτομεί τις
διχοτομεί τις  και
και  , έχουμε πως
, έχουμε πως  .
.Άρα
 και ακόμη έχουμε πως
και ακόμη έχουμε πως 
Εφαρμόζοντας το αντίστροφο θεώρημα
 στο τρίγωνο
στο τρίγωνο  , προκύπτει ότι η
, προκύπτει ότι η  και
και  συντρέχουν, δηλαδή η
συντρέχουν, δηλαδή η  και
και  συντρέχουν.
συντρέχουν.Edit: Κάποιες βελτιώσεις... Όσο για το σχήμα... ενώ το σχεδίαζα είδα ότι με πρόλαβε ο κύριος Νίκος παρακάτω...
τελευταία επεξεργασία από Διονύσιος Αδαμόπουλος σε Πέμ Μάιος 04, 2017 6:58 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Houston, we have a problem!
Re: BMO 2017 - Θέματα
Η Διοφαντική  έχει ως λύσεις και τις
έχει ως λύσεις και τις  οι οποίες φυσικά δεν επαληθεύουν την αρχική.
οι οποίες φυσικά δεν επαληθεύουν την αρχική.
 έχει ως λύσεις και τις
έχει ως λύσεις και τις  οι οποίες φυσικά δεν επαληθεύουν την αρχική.
οι οποίες φυσικά δεν επαληθεύουν την αρχική.Κωνσταντίνος Μεταξάς
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: BMO 2017 - Θέματα
Προφανώς, ταSoteris έγραψε:Πρόβλημα 2
Έστωοξυγώνιο τρίγωνο με
και έστω
ο περιγεγραμμένος κύκλος του. Έστω
και
οι εφαπτομένες του κύκλου
στα σημεία
και
, αντίστοιχα, και έστω
το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την πλευρά
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την ευθεία
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
.
Να αποδείξετε ότι οι ευθείεςκαι
συντρέχουν.
(Ελλάδα)
 είναι ισοσκελή τραπέζια.
είναι ισοσκελή τραπέζια.Είναι
 .
.Επίσης,
 .
.Είναι λοιπόν
 , άρα τα
, άρα τα  είναι όμοια.
είναι όμοια.Έτσι,
 , οπότε
, οπότε  .
.Από Θ.Θαλή,
 (1).
(1).Έστω
 το σημείο τομής της
το σημείο τομής της  με την
με την  .
.Προφανώς,
 , και εύκολα
, και εύκολα  .
.Με χρήση Ν.Ημιτόνων στα
 και διαίρεση κατά μέλη έχουμε
και διαίρεση κατά μέλη έχουμε  (2).
(2).Όμως,
 , οπότε
, οπότε  (3).
(3).Είναι
 , άρα
, άρα  (4).
(4).Από (4) και το γεγονός ότι
 , έχουμε
, έχουμε  (5), με
(5), με  το σημείο τομής της
το σημείο τομής της  με την
με την 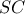 .
.Από (1), (5) έχουμε ότι στο τρίγωνο
 αληθεύει το αντίστροφο Θ.Ceva, οπότε οι
αληθεύει το αντίστροφο Θ.Ceva, οπότε οι  συντρέχουν, οπότε το ζητούμενο είναι άμεσο.
συντρέχουν, οπότε το ζητούμενο είναι άμεσο. Κερδίζουμε ό,τι τολμούμε!
Re: BMO 2017 - Θέματα
Ωραία η λύση σου ΔιονύσηΔιονύσιος Αδαμόπουλος έγραψε:Θα αποδείξουμε πως οι περιγεγραμμένοι κύκλοι τωνSoteris έγραψε:
Πρόβλημα 2
Έστωοξυγώνιο τρίγωνο με
και έστω
ο περιγεγραμμένος κύκλος του. Έστω
και
οι εφαπτομένες του κύκλου
στα σημεία
και
, αντίστοιχα, και έστω
το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την πλευρά
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την ευθεία
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
.
Να αποδείξετε ότι οι ευθείεςκαι
συντρέχουν.
(Ελλάδα)
και
εφάπτονται των
και
αντίστοιχα.
Αν πάρουμε ένα τυχαίο σημείοστην προέκταση της
, τότε αρκεί να δείξουμε πως
.
Με άλλα λόγια αρκεί:

, που ισχύει.
Πράγματι λοιπόν οι περιγεγραμμένοι κύκλοι τωνκαι
εφάπτονται των
και
αντίστοιχα.
Ακόμη ηείναι αντιπαράλληλη της
στο τρίγωνο
(έχουμε το εκφυλισμένο εγγράψιμο
). Άρα η συμμετροδιάμεσος της κορυφής
, δηλαδή η
περνάει από το μέσο του
, έστω
. Όμοια η
περνάει και από το μέσο
της
.
Από τη δέσμη, επειδή η
διχοτομεί τις
και
, έχουμε πως
.
Άρακαι ακόμη έχουμε πως
Εφαρμόζοντας το θεώρημαστο τρίγωνο
, προκύπτει ότι η
και
συντρέχουν, δηλαδή η
και
συντρέχουν.
Αργότερα θα βάλω το σχήμα...
Τη λύση του Ορέστη στο ίδιο πρόβλημα την είδα φευγαλέα και σ αυτόν
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: BMO 2017 - Θέματα
Ναι σωστάknm2608 έγραψε:Η Διοφαντικήέχει ως λύσεις και τις
οι οποίες φυσικά δεν επαληθεύουν την αρχική.
Κερδίζουμε ό,τι τολμούμε!
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13273
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: BMO 2017 - Θέματα
Το σκεπτικό: ΈστωSoteris έγραψε: Πρόβλημα 2
Έστωοξυγώνιο τρίγωνο με
και έστω
ο περιγεγραμμένος κύκλος του. Έστω
και
οι εφαπτομένες του κύκλου
στα σημεία
και
, αντίστοιχα, και έστω
το σημείο τομής τους. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Η ευθεία που διέρχεται από το σημείο
και είναι παράλληλη προς την
τέμνει την
στο σημείο
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την πλευρά
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
. Ο περιγεγραμμένος κύκλος στο τρίγωνο
τέμνει την ευθεία
σε σημείο
, με το
να βρίσκεται ανάμεσα στα
και
.
Να αποδείξετε ότι οι ευθείεςκαι
συντρέχουν.
(Ελλάδα)
 το σημείο τομής των
το σημείο τομής των  Αρκεί να δείξω ότι
Αρκεί να δείξω ότι  Τότε η
Τότε η  θα είναι συμμετροδιάμεσος, άρα το
θα είναι συμμετροδιάμεσος, άρα το  θα είναι σημείο και της
θα είναι σημείο και της  Η απόδειξη επιγραμματικά δίνεται από τα παρακάτω βήματα:
● Η
Η απόδειξη επιγραμματικά δίνεται από τα παρακάτω βήματα:
● Η  εφάπτεται στον μπλε κύκλο και η
εφάπτεται στον μπλε κύκλο και η  στον πράσινο:
στον πράσινο: 
 και
και 

● Μενέλαος στο
 με διατέμνουσα
με διατέμνουσα 


ΥΓ. Συμπτωματικά, ήθελα να ανεβάσω μία άσκηση με συμμετροδιάμεσο σήμερα, αλλά την αφήνω για άλλη φορά.
Re: BMO 2017 - Θέματα
Τα συγχαρητήριά μου στον Δημήτρη για το όμορφο πρόβλημα 4!
Το πρόβλημα 2 όντως προτάθηκε από κοινού από τον Βαγγέλη Ψύχα και εμένα.
Γενικά βρήκα πολύ εύκολο το πρόβλημα 1 για το επίπεδο του διαγωνισμού.
Θα βάλω τις λύσεις μου αύριο γιατί τώρα είμαι από κινητό.
Υ.γ. Μετά τη Jbmo του 2015 είναι η δεύτερη φορά που ελληνικό θέμα είναι το 2 και κυπριακό το 4
Το πρόβλημα 2 όντως προτάθηκε από κοινού από τον Βαγγέλη Ψύχα και εμένα.
Γενικά βρήκα πολύ εύκολο το πρόβλημα 1 για το επίπεδο του διαγωνισμού.
Θα βάλω τις λύσεις μου αύριο γιατί τώρα είμαι από κινητό.
Υ.γ. Μετά τη Jbmo του 2015 είναι η δεύτερη φορά που ελληνικό θέμα είναι το 2 και κυπριακό το 4
τελευταία επεξεργασία από silouan σε Παρ Μάιος 05, 2017 4:27 am, έχει επεξεργασθεί 1 φορά συνολικά.
Σιλουανός Μπραζιτίκος
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: BMO 2017 - Θέματα
Όντως το πρώτο θέμα είναι πανεύκολο. Μήπως όμως μας ξεγελά γιατί το έχουμε δεί πολλές φορές στην Ελλάδα?silouan έγραψε:Το όμορφο πρόβλημα 4 προτάθηκε από τον Δημήτρη Χριστοφίδη. Δημήτρη συγχαρητήρια!
Το πρόβλημα 2 προτάθηκε από κοινού από τον Βαγγέλη Ψύχα και εμένα.
Γενικά βρήκα πολύ εύκολο το πρόβλημα 1 για το επίπεδο του διαγωνισμού.
Θα βάλω τις λύσεις μου αύριο γιατί τώρα είμαι από κινητό.
Συγχαρητήρια και στους 3 σας, για τα 2 υπέροχα θέματα!!!
Re: BMO 2017 - Θέματα
Από τα 3 πρώτα, μόνο η γεωμετρία μου φάνηκε να έχει κάποια δυσκολία (ίσως επειδή δεν έχω ασχοληθεί και τόσο με γεωμετρίες), οπότε θα βάλω μια λύση:
Ας υποθέσουμε ότι η εφαπτομένη του περιγεγραμμένου του στο
στο  τέμνει την
τέμνει την  στο
στο  , και η
, και η  τέμνει την
τέμνει την  στο
στο  . Είναι γνωστό πως η
. Είναι γνωστό πως η  είναι αρμονική.
είναι αρμονική.
Αν λοιπόν η τέμνει την
τέμνει την  στο
στο  , αρκεί
, αρκεί  να είναι επίσης αρμονική, αφού από τη μοναδικότητα του αρμονικού συζηγούς θα έχουμε
να είναι επίσης αρμονική, αφού από τη μοναδικότητα του αρμονικού συζηγούς θα έχουμε  .
.
Από παραλληλίες, υπολογισμούς γωνιών χορδών - εφαπτομένων από τις αντίστοιχες εγγεγραμμένες, και από το εγγεγραμμένο , έχουμε
, έχουμε  .
.
Ομοίως, δουλεύοντας με τον κύκλο του , βγάζουμε
, βγάζουμε  .
.
Άρα τα και
και  είναι όμοια, όπως και τα
είναι όμοια, όπως και τα  και
και  . Από τις ομοιότητες αυτές έχουμε
. Από τις ομοιότητες αυτές έχουμε  και από Θαλή ο λόγος αυτός είναι
και από Θαλή ο λόγος αυτός είναι  , οπότε πράγματι
, οπότε πράγματι  είναι αρμονική και τελειώσαμε.
είναι αρμονική και τελειώσαμε.
Ας υποθέσουμε ότι η εφαπτομένη του περιγεγραμμένου του
 στο
στο  τέμνει την
τέμνει την  στο
στο  , και η
, και η  τέμνει την
τέμνει την  στο
στο  . Είναι γνωστό πως η
. Είναι γνωστό πως η  είναι αρμονική.
είναι αρμονική.Αν λοιπόν η
 τέμνει την
τέμνει την  στο
στο  , αρκεί
, αρκεί  να είναι επίσης αρμονική, αφού από τη μοναδικότητα του αρμονικού συζηγούς θα έχουμε
να είναι επίσης αρμονική, αφού από τη μοναδικότητα του αρμονικού συζηγούς θα έχουμε  .
.Από παραλληλίες, υπολογισμούς γωνιών χορδών - εφαπτομένων από τις αντίστοιχες εγγεγραμμένες, και από το εγγεγραμμένο
 , έχουμε
, έχουμε  .
.Ομοίως, δουλεύοντας με τον κύκλο του
 , βγάζουμε
, βγάζουμε  .
.Άρα τα
 και
και  είναι όμοια, όπως και τα
είναι όμοια, όπως και τα  και
και  . Από τις ομοιότητες αυτές έχουμε
. Από τις ομοιότητες αυτές έχουμε  και από Θαλή ο λόγος αυτός είναι
και από Θαλή ο λόγος αυτός είναι  , οπότε πράγματι
, οπότε πράγματι  είναι αρμονική και τελειώσαμε.
είναι αρμονική και τελειώσαμε.Κολλιοπουλος Νικος.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
Μεταδιδακτορικός ερευνητής.
Ερευνητικά ενδιαφέροντα: Στοχαστικές ΜΔΕ, ασυμπτωτική ανάλυση στοχαστικών συστημάτων, εφαρμογές αυτών στα χρηματοοικονομικά και στη διαχείριση ρίσκων.
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
Re: BMO 2017 - Θέματα
Θέλω και εγώ να συγχαρώ με τη σειρά μου τους κ.Σιλουανό και Ψύχα για την ωραία γεωμετρία καθώς και τον κ.Δημήτρη για το 4ο πρόβλημα!
Ένα επιπλέον ερώτημα προς επίλυση για τη γεωμετρία (το παρατήρησα την ώρα του διαγωνισμού αλλά δε μου χρειάστηκε):
Αν η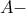 διάμεσος του τριγώνου
διάμεσος του τριγώνου  τέμνει τον
τέμνει τον  στο
στο  να δειχθεί ότι τα σημεία
να δειχθεί ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.
Καλά αποτελέσματα στις ομάδες της Ελλάδας και της Κύπρου!
Ένα επιπλέον ερώτημα προς επίλυση για τη γεωμετρία (το παρατήρησα την ώρα του διαγωνισμού αλλά δε μου χρειάστηκε):
Αν η
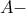 διάμεσος του τριγώνου
διάμεσος του τριγώνου  τέμνει τον
τέμνει τον  στο
στο  να δειχθεί ότι τα σημεία
να δειχθεί ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.Καλά αποτελέσματα στις ομάδες της Ελλάδας και της Κύπρου!
Σημαντήρης Γιάννης
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: BMO 2017 - Θέματα
Δεν ξέρω αν θα έπρεπε να ξεφεύγουμε (ειδικά σε αυτό το θέμα) ...simantiris j. έγραψε:Θέλω και εγώ να συγχαρώ με τη σειρά μου τους κ.Σιλουανό και Ψύχα για την ωραία γεωμετρία καθώς και τον κ.Δημήτρη για το 4ο πρόβλημα!
Ένα επιπλέον ερώτημα προς επίλυση για τη γεωμετρία (το παρατήρησα την ώρα του διαγωνισμού αλλά δε μου χρειάστηκε):
Αν ηδιάμεσος του τριγώνου
τέμνει τον
στο
να δειχθεί ότι τα σημεία
είναι ομοκυκλικά.
Καλά αποτελέσματα στις ομάδες της Ελλάδας και της Κύπρου!
... ωστόσο η παραπάνω παρατήρηση ισχύει:
Θεωρούμε συμμετρική αντιστροφή με πόλο την κορυφή
 , δύναμη
, δύναμη  και άξονα την διχοτόμο της
και άξονα την διχοτόμο της  .
.Τότε τα
 και
και  αντιστρέφονται, άρα έχουμε πως και οι ευθείες
αντιστρέφονται, άρα έχουμε πως και οι ευθείες  και
και  αντιστρέφονται.
αντιστρέφονται.Ο κύκλος
 γίνεται η
γίνεται η  , ενώ η συμμετροδιάμεσος
, ενώ η συμμετροδιάμεσος  γίνεται η διάμεσος
γίνεται η διάμεσος  . Επειδή το
. Επειδή το  ανήκει στον κύκλο
ανήκει στον κύκλο  , έχουμε πως το αντίστροφο του
, έχουμε πως το αντίστροφο του  , έστω
, έστω  , ανήκει στην
, ανήκει στην  , αλλά και στην συμμετροδιάμεσο
, αλλά και στην συμμετροδιάμεσο  , δηλαδή είναι η τομή τους. Σύμφωνα με την αρχική άσκηση, τα
, δηλαδή είναι η τομή τους. Σύμφωνα με την αρχική άσκηση, τα  είναι συνευθειακά. Άρα τα αντίστροφα τους
είναι συνευθειακά. Άρα τα αντίστροφα τους  και ο πόλος
και ο πόλος  θα είναι ομοκυκλικά σημεία.
θα είναι ομοκυκλικά σημεία. Ακόμη οι περιγεγραμμένοι κύκλοι των
 και
και  , που εφάπτονται των
, που εφάπτονται των  και
και  αντίστοιχα, γίνονται κύκλοι που εφάπτονται των
αντίστοιχα, γίνονται κύκλοι που εφάπτονται των  και
και  αντίστοιχα άρα αντιστρέφονται. Επομένως αφού τα
αντίστοιχα άρα αντιστρέφονται. Επομένως αφού τα  είναι τα σημεία τομής τους με τις αντίστροφες ευθείες
είναι τα σημεία τομής τους με τις αντίστροφες ευθείες  και
και  , έχουμε πως τα
, έχουμε πως τα  είναι αντίστροφα. Επομένως το
είναι αντίστροφα. Επομένως το  είναι το
είναι το  και το
και το  είναι το
είναι το  .
. Πράγματι λοιπόν τα
 είναι ομοκυκλικά.
είναι ομοκυκλικά.Houston, we have a problem!
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: BMO 2017 - Θέματα
Με ιδιαίτερη χαρά σας παρουσιάζω τα αποτελέσματα της Ελληνικής και Κυπριακής Αποστολής στην Οχρίδα της Π.Γ.Δ.Μ.
Τα cut offs των μεταλλίων ήταν 39 για το Χρυσό, 31 για το Αργυρό και 16 για το Χάλκινο.
Ελλάδα
Βασίλης Γεωργιάδης: 40/40 Χρυσό Μετάλλιο
Δημήτρης Μελάς: 32/40 Αργυρό Μετάλλιο
Ραφαήλ Τσιάμης: 31/40 Αργυρό Μετάλλιο
Ραφαήλ Ψυρούκης: 30/40 Χάλκινο Μετάλλιο
Δημήτρης Λώλας: 27/40 Χάλκινο Μετάλλιο
Σωτήρης Παπασωτηρίου: 14/40 Εύφημη Μνεία
Να συγχαρώ όλα τα παιδιά για την εξαιρετική τους επίδοση και εμφάνιση στο διαγωνισμό και ιδιαίτερα τον Βασίλη για το Perfect Score που κατάφερε!! Μπράβο σε όλη την Ελληνική Ομάδα που αξίζει να αναφέρουμε ότι έλυσε ΠΛΗΡΩΣ το θέμα της Γεωμετρίας συνεχίζοντας την καλή παράδοση παρά το ότι η χώρα προσπαθεί να την εξοβελίσει από το πρόγραμμα σπουδών υποβαθμίζοντάς τη συνεχώς!
Κύπρος
Άγγελος Άσσος: 24/40 Χάλκινο Μετάλλιο
Αλέξανδρος
Τα cut offs των μεταλλίων ήταν 39 για το Χρυσό, 31 για το Αργυρό και 16 για το Χάλκινο.
Ελλάδα
Βασίλης Γεωργιάδης: 40/40 Χρυσό Μετάλλιο
Δημήτρης Μελάς: 32/40 Αργυρό Μετάλλιο
Ραφαήλ Τσιάμης: 31/40 Αργυρό Μετάλλιο
Ραφαήλ Ψυρούκης: 30/40 Χάλκινο Μετάλλιο
Δημήτρης Λώλας: 27/40 Χάλκινο Μετάλλιο
Σωτήρης Παπασωτηρίου: 14/40 Εύφημη Μνεία
Να συγχαρώ όλα τα παιδιά για την εξαιρετική τους επίδοση και εμφάνιση στο διαγωνισμό και ιδιαίτερα τον Βασίλη για το Perfect Score που κατάφερε!! Μπράβο σε όλη την Ελληνική Ομάδα που αξίζει να αναφέρουμε ότι έλυσε ΠΛΗΡΩΣ το θέμα της Γεωμετρίας συνεχίζοντας την καλή παράδοση παρά το ότι η χώρα προσπαθεί να την εξοβελίσει από το πρόγραμμα σπουδών υποβαθμίζοντάς τη συνεχώς!
Κύπρος
Άγγελος Άσσος: 24/40 Χάλκινο Μετάλλιο
Αλέξανδρος
Αλέξανδρος Συγκελάκης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
