Να βρείτε όλες τις ακέραιες λύσεις
 της εξίσωσης
της εξίσωσης
Προβλήμα 2
Αν
 είναι θετικοί πραγματικοί αριθμοί , να βρείτε την μεγιστή τιμή του
είναι θετικοί πραγματικοί αριθμοί , να βρείτε την μεγιστή τιμή του  , έτσι ώστε
, έτσι ώστε
Προβλήμα 3
Ο εγγεγραμμένος κύκλος του σκαληνού τριγώνου
 , με
, με  , εφάπτεται των πλευρών
, εφάπτεται των πλευρών  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Το σημείο
αντίστοιχα. Το σημείο  είναι το μέσο της ευθείας
είναι το μέσο της ευθείας  , και το σημείο
, και το σημείο  είναι το εγκέντρο του του τριγώνου
είναι το εγκέντρο του του τριγώνου  . Αν οι ευθείες
. Αν οι ευθείες  και
και  τέμνουν η ευθεία,
τέμνουν η ευθεία,  στα σημεία
στα σημεία  και
και  αντίστοιχα, να δείξετε ότι το τρίγωνο
αντίστοιχα, να δείξετε ότι το τρίγωνο  είναι ισόπλευρο.
είναι ισόπλευρο.
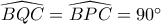 .
. , άρα
, άρα  (1).
(1). (2).
(2). , άρα
, άρα  (3).
(3).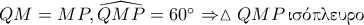 .
.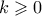 ισχύει η (1).
ισχύει η (1). (2)
(2)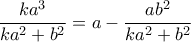 και τα κυκλικά, άρα
και τα κυκλικά, άρα 
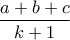 .
.![ka^2+b^2=a^2+a^2 + \ldots a^2+b^2+b^2 \geqslant (k+1) \sqrt[k+1]{a^{2k}b^2} ka^2+b^2=a^2+a^2 + \ldots a^2+b^2+b^2 \geqslant (k+1) \sqrt[k+1]{a^{2k}b^2}](/forum/ext/geomar/texintegr/latexrender/pictures/baec6c164e5964d68cfa38fd31a290b6.png) , άρα
, άρα ![\displaystyle \sum \dfrac{ab^2}{ka^2+b^2} \leqslant \sum \dfrac{\sqrt[k+1]{a^{1-k}b^{2k}}}{k+1} \leqslant \sum \dfrac{a(1-k)+2bk}{(k+1)^2}= \displaystyle \sum \dfrac{ab^2}{ka^2+b^2} \leqslant \sum \dfrac{\sqrt[k+1]{a^{1-k}b^{2k}}}{k+1} \leqslant \sum \dfrac{a(1-k)+2bk}{(k+1)^2}=](/forum/ext/geomar/texintegr/latexrender/pictures/e6a68cf23a9a443a2899657df7ed499a.png)
![\dfrac{\displaystyle \sum [a(1-k)+2bk]}{(k+1)^2}=\dfrac{a+b+c}{k+1} \dfrac{\displaystyle \sum [a(1-k)+2bk]}{(k+1)^2}=\dfrac{a+b+c}{k+1}](/forum/ext/geomar/texintegr/latexrender/pictures/720769e83a8a994f13a190ace4b2e460.png) , και η αρχική ανισότητα αποδείχτηκε.
, και η αρχική ανισότητα αποδείχτηκε. ;
;![\displaystyle \sum \dfrac{ab^2}{ka^2+b^2} \leqslant \sum \dfrac{\sqrt[k+1]{a^{1-k}b^{2k}}}{k+1} \leqslant \color{red} \sum \dfrac{a(1-k)+2bk}{(k+1)^2}= \displaystyle \sum \dfrac{ab^2}{ka^2+b^2} \leqslant \sum \dfrac{\sqrt[k+1]{a^{1-k}b^{2k}}}{k+1} \leqslant \color{red} \sum \dfrac{a(1-k)+2bk}{(k+1)^2}=](/forum/ext/geomar/texintegr/latexrender/pictures/f51b9a903bddedf54140fccad7a348ad.png)
 σε αυτό το βήμα.
σε αυτό το βήμα.



 δεν είναι υπόλοιπο του
δεν είναι υπόλοιπο του  με το
με το  (Αν δεν κάνω λάθος...
(Αν δεν κάνω λάθος...  .
. άρτιος. Έστω
άρτιος. Έστω  .
.
 άρτιος, έστω
άρτιος, έστω  :
:

 , που είναι άτοπο σε όλες τις παραπάνω περιπτώσεις.
, που είναι άτοπο σε όλες τις παραπάνω περιπτώσεις. 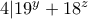 και αφού
και αφού  . Άρα
. Άρα  , δηλαδή
, δηλαδή  άρτιος, έστω
άρτιος, έστω  .
.
 . Άρα μια από τις δύο θα είναι
. Άρα μια από τις δύο θα είναι  και η άλλη
και η άλλη  . Προφανώς έχουμε πως
. Προφανώς έχουμε πως  και ότι
και ότι  , άρα
, άρα  .
. έχουμε πως το
έχουμε πως το  διαιρεί το
διαιρεί το  σε μέγιστη δύναμη
σε μέγιστη δύναμη  , καθώς ο
, καθώς ο  σε μέγιστη δύναμη
σε μέγιστη δύναμη  . Άρα αναγκαστικά
. Άρα αναγκαστικά  .
.  , που δεν έχει λύσεις.
, που δεν έχει λύσεις.  (1)
(1)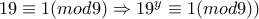 (2)
(2) (3)
(3) , το οποίο δεν ισχύει για κανέναν ακέραιο.
, το οποίο δεν ισχύει για κανέναν ακέραιο. είναι προφανώς ισόπλευρο και άρα τα
είναι προφανώς ισόπλευρο και άρα τα  βλέπουν υπό ίσες και
βλέπουν υπό ίσες και  την
την  , όθεν το τετράπλευρο
, όθεν το τετράπλευρο  είναι εγγράψιμο , συνεπώς
είναι εγγράψιμο , συνεπώς  . Ομοίως
. Ομοίως  . Τώρα θα είναι
. Τώρα θα είναι  . Αφού όμως η
. Αφού όμως η είναι εξωτερική στο ισοσκελές τρίγωνο
είναι εξωτερική στο ισοσκελές τρίγωνο 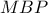 θα είναι
θα είναι  και ομοίως
και ομοίως  .
. και άρα το
και άρα το  είναι ισόπλευρο.
είναι ισόπλευρο.