Panagiotis11 έγραψε:
Πρόβλημα 3. O Νίκος ζωγραφίζει το γράμμα

στα κελιά ενός τετράγωνου πλέγματος.Παρόλα αυτά δεν θέλει να ζωγραφίσει το

σε

συνεχόμενα κελιά(οριζόντια,κάθετα ή διαγώνια).Να βρείτε όλους τους πραγματικούς αριθμούς

τέτοιοι ώστε για κάθε θετικό ακέραιο

,ο Νίκος να μπορέσει να σημειώσει τουλάχιστον
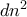
κελιά ενός τετραγώνου

Η απάντηση είναι
![d \in (0,1/2] d \in (0,1/2]](/forum/ext/geomar/texintegr/latexrender/pictures/f560d75b0b2b97954e160eb9c11da934.png)
.
Κοιτάζω αρχικά ορθογώνια της μορφής

. Θα ονομάζω ένα τέτοιο ορθογώνιο καλό αν έχει σημειωμένο το γράμμα

είτε μόνο στο πάνω κελί είτε μόνο στο κάτω κελί.
Λήμμα 1: Σε κάθε

ορθογώνιο μπορώ να σημειώσω το

το πολύ
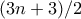
σε κελιά.
Σκιαγράφηση απόδειξης: Έστω ότι το

ορθογώνιο έχει καλά ορθογώνια στις στήλες

. Ισχυρίζομαι τα εξής:
(α) Στις πρώτες

στήλες το

σημειώθηκε το πολύ σε

κελιά. Επίσης στις πρώτες

στήλες, για

το

σημειώθηκε το πολύ σε

κελιά.
(β) Για κάθε

, στις στήλες
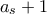
ως

το

σημειώθηκε το πολύ σε

κελιά. Επίσης στις στήλες

στήλες, για

το

σημειώθηκε το πολύ σε

κελιά.
Από τα (α) και (β) το Λήμμα 1 έπεται άμεσα. Η απόδειξη των (α) και (β) έχει αρκετή περιπτωσιολογία με αρκετά σχήματα οπότε θα αποφύγω να την παραθέσω. Ουσιαστικά κοιτάζει τι ορθογώνια της μορφής

μπορώ να έχω στην σειρά. Π.χ αν ξεκινήσω με δυο

ορθογώνια τα οποία έχουν από δύο

σημειωμένα το κάθε ένα, τότε υπάρχουν αρκετοί περιορισμοί στο τι

ορθογώνιο μπορεί να ακολουθήσει που περιορίζει τον αριθμό των

που μπορώ να έχω.
Το Λήμμα 1 είναι το βασικότερο λήμμα της άσκησης. Τα υπόλοιπα είναι απλά. Σε ένα

τετράγωνο όπου

με

, από το Λήμμα 1 μπορώ να έχω το πολύ

σημειωμένα

στο άνω αριστερά

ορθογώνιο και άρα το πολύ

σημειωμένα

σε όλο το τετράγωνο. Όμως

Οπότε σίγουρα δεν μπορούμε να έχουμε

. Μπορούμε να επιτύχουμε

με την εξής επιλογή: Στις περιττές στήλες, σημειώνουμε

στα σειρές

και

. Στις άρτιες στήλες σημειώνουμε

στα σειρές

και

.
 είναι θετικοί ακέραιοι με γινόμενο
είναι θετικοί ακέραιοι με γινόμενο  ,όπου
,όπου  είναι ένας περιττός θετικός ακέραιος,να αποδείξετε ότι:
είναι ένας περιττός θετικός ακέραιος,να αποδείξετε ότι: 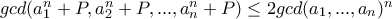
 με ορθόκεντρο
με ορθόκεντρο  και
και  μέσο
μέσο  .Υποθέτουμε ότι
.Υποθέτουμε ότι  σημεία του κύκλου με διάμετρο
σημεία του κύκλου με διάμετρο  ,διαφορετικά από το
,διαφορετικά από το  ,τέτοια ώστε το
,τέτοια ώστε το  να βρίσκεται πάνω στην
να βρίσκεται πάνω στην  .Να αποδείξετε ότι το ορθόκεντρο του
.Να αποδείξετε ότι το ορθόκεντρο του  βρίσκεται πάνω στο στον περιγγεγραμένο κύκλο του
βρίσκεται πάνω στο στον περιγγεγραμένο κύκλο του 
 στα κελιά ενός τετράγωνου πλέγματος.Παρόλα αυτά δεν θέλει να ζωγραφίσει το
στα κελιά ενός τετράγωνου πλέγματος.Παρόλα αυτά δεν θέλει να ζωγραφίσει το  σε
σε  συνεχόμενα κελιά(οριζόντια,κάθετα ή διαγώνια).Να βρείτε όλους τους πραγματικούς αριθμούς
συνεχόμενα κελιά(οριζόντια,κάθετα ή διαγώνια).Να βρείτε όλους τους πραγματικούς αριθμούς 
 ,ο Νίκος να μπορέσει να σημειώσει τουλάχιστον
,ο Νίκος να μπορέσει να σημειώσει τουλάχιστον 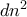 κελιά ενός τετραγώνου
κελιά ενός τετραγώνου 

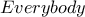 -
-  -
-  -
-  -
- 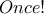
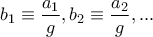 όπου
όπου  και έχουμε
και έχουμε  .
. .
. , τότε
, τότε  για κάποιο
για κάποιο  . Έτσι
. Έτσι  και έχουμε άτοπο.
και έχουμε άτοπο. , τότε
, τότε  και πολλαπλασιάζοντας κατά μέλη έχουμε
και πολλαπλασιάζοντας κατά μέλη έχουμε  (αφού ο
(αφού ο 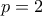 . Θέτοντας το
. Θέτοντας το  στη θέση του
στη θέση του  βλέπουμε επίσης ότι
βλέπουμε επίσης ότι  .
.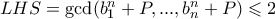 .
. του
του  φέρνουμε από το
φέρνουμε από το  (οπότε παράλληλη στην
(οπότε παράλληλη στην  ) και ομοίως από το
) και ομοίως από το  παράλληλη στην
παράλληλη στην 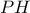 . Έτσι, το
. Έτσι, το 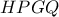 είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. το μέσο του
το μέσο του  και το
και το  μέσο του
μέσο του  είναι ορθή και, αφού το
είναι ορθή και, αφού το  είναι διάμετρος του κύκλου Euler του
είναι διάμετρος του κύκλου Euler του  , το
, το  . Επειδή ο κύκλος του Euler διχοτομεί κάθε ευθύγραμμο τμήμα που ενώνει το ορθόκεντρο με τον περιγεγραμμένο κύκλο, συμπεραίνουμε ότι το
. Επειδή ο κύκλος του Euler διχοτομεί κάθε ευθύγραμμο τμήμα που ενώνει το ορθόκεντρο με τον περιγεγραμμένο κύκλο, συμπεραίνουμε ότι το  αν
αν  είναι το κέντρο του περιγεγραμμένου κύκλου στο τρίγωνο
είναι το κέντρο του περιγεγραμμένου κύκλου στο τρίγωνο  και τμήσει τον μεν περιγεγραμμένο κύκλο στο τρίγωνο
και τμήσει τον μεν περιγεγραμμένο κύκλο στο τρίγωνο  τον δε κύκλο
τον δε κύκλο  στο
στο  , αρκεί τα
, αρκεί τα 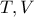 να είναι συμμετρικά ως προς την
να είναι συμμετρικά ως προς την  .
.![d \in (0,1/2] d \in (0,1/2]](/forum/ext/geomar/texintegr/latexrender/pictures/f560d75b0b2b97954e160eb9c11da934.png) .
. . Θα ονομάζω ένα τέτοιο ορθογώνιο καλό αν έχει σημειωμένο το γράμμα
. Θα ονομάζω ένα τέτοιο ορθογώνιο καλό αν έχει σημειωμένο το γράμμα  ορθογώνιο μπορώ να σημειώσω το
ορθογώνιο μπορώ να σημειώσω το 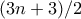 σε κελιά.
σε κελιά.  . Ισχυρίζομαι τα εξής:
. Ισχυρίζομαι τα εξής:  στήλες το
στήλες το  σημειώθηκε το πολύ σε
σημειώθηκε το πολύ σε  κελιά. Επίσης στις πρώτες
κελιά. Επίσης στις πρώτες  στήλες, για
στήλες, για  το
το  κελιά.
κελιά.  , στις στήλες
, στις στήλες 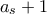 ως
ως  το
το  κελιά. Επίσης στις στήλες
κελιά. Επίσης στις στήλες  στήλες, για
στήλες, για  το
το  κελιά.
κελιά.  ορθογώνιο μπορεί να ακολουθήσει που περιορίζει τον αριθμό των
ορθογώνιο μπορεί να ακολουθήσει που περιορίζει τον αριθμό των  με
με  , από το Λήμμα 1 μπορώ να έχω το πολύ
, από το Λήμμα 1 μπορώ να έχω το πολύ  σημειωμένα
σημειωμένα  ορθογώνιο και άρα το πολύ
ορθογώνιο και άρα το πολύ  σημειωμένα
σημειωμένα 
 . Μπορούμε να επιτύχουμε
. Μπορούμε να επιτύχουμε  με την εξής επιλογή: Στις περιττές στήλες, σημειώνουμε
με την εξής επιλογή: Στις περιττές στήλες, σημειώνουμε  και
και  . Στις άρτιες στήλες σημειώνουμε
. Στις άρτιες στήλες σημειώνουμε  και
και  .
.