IMO 2017
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: IMO 2017
Το πρόβλημα 1 είναι
Για κάθε ακέραιο , ορίζουμε την ακολουθία
, ορίζουμε την ακολουθία  ως εξής:
ως εξής:

Να προσδιορίσετε όλες τις τιμές του για τις οποίες υπάρχει αριθμός
για τις οποίες υπάρχει αριθμός  τέτοιος ώστε
τέτοιος ώστε  για άπειρες τιμές του
για άπειρες τιμές του  .
.
Επεξεργασία από Demetres: Βελτίωση εκφώνησης.
συμπλήρωμα. Διόρθωσα καραμπινάτο τυπογραφικό.
συμπλήρωμα2.Το τυπογραφικό είχε γίνει από τον Demetres όταν βελτίωσε την εκφώνηση.
Για κάθε ακέραιο
 , ορίζουμε την ακολουθία
, ορίζουμε την ακολουθία  ως εξής:
ως εξής:
Να προσδιορίσετε όλες τις τιμές του
 για τις οποίες υπάρχει αριθμός
για τις οποίες υπάρχει αριθμός  τέτοιος ώστε
τέτοιος ώστε  για άπειρες τιμές του
για άπειρες τιμές του  .
.Επεξεργασία από Demetres: Βελτίωση εκφώνησης.
συμπλήρωμα. Διόρθωσα καραμπινάτο τυπογραφικό.
συμπλήρωμα2.Το τυπογραφικό είχε γίνει από τον Demetres όταν βελτίωσε την εκφώνηση.
τελευταία επεξεργασία από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ σε Τετ Ιούλ 19, 2017 1:23 pm, έχει επεξεργασθεί 2 φορές συνολικά.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: IMO 2017
Πρόβλημα 3
Ένας κυνηγός και ένα αόρατο κουνέλι παίζουν ένα παιγνίδι στο Ευκλείδειο επίπεδο. Το σημείο εκκίνησης του κουνελιού και το σημείο εκκίνησης
του κουνελιού και το σημείο εκκίνησης  του κυνηγού είναι τα ίδια. Μετά από
του κυνηγού είναι τα ίδια. Μετά από  γύρους του παιγνιδιού, το κουνέλι βρίσκεται στο σημείο
γύρους του παιγνιδιού, το κουνέλι βρίσκεται στο σημείο  και ο κυνηγός στο σημείο
και ο κυνηγός στο σημείο  . Στον
. Στον  -οστό γύρο του παιγνιδιού, τρία πράγματα συμβαίνουν κατά σειρά:
-οστό γύρο του παιγνιδιού, τρία πράγματα συμβαίνουν κατά σειρά:
(α) Το κουνέλι κινείται αόρατα σε ένα σημείο τέτοιο ώστε η απόσταση μεταξύ των σημείων
τέτοιο ώστε η απόσταση μεταξύ των σημείων  και
και  να είναι ακριβώς ίση με
να είναι ακριβώς ίση με  .
.
(β) Μια συσκευή παρακολούθησης αναφέρει ένα σημείο στον κυνηγό. Η μόνη εγγυημένη πληροφορία είναι ότι η απόσταση μεταξύ των σημείων
στον κυνηγό. Η μόνη εγγυημένη πληροφορία είναι ότι η απόσταση μεταξύ των σημείων  και
και  είναι το πολύ
είναι το πολύ  .
.
(γ) Ο κυνηγός κινείται ορατά σε ένα σημείο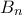 τέτοιο ώστε η απόσταση μεταξύ των σημείων
τέτοιο ώστε η απόσταση μεταξύ των σημείων  και
και 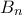 να είναι ακριβώς ίση με
να είναι ακριβώς ίση με  .
.
Είναι πάντοτε δυνατόν, ανεξάρτητα από το πως κινείται το κουνέλι και ανεξάρτητα από το ποια σημεία αναφέρονται από την συσκευή παρακολούθησης , για τον κυνηγό να επιλέξει τις κινήσεις του έτσι ώστε μετά από γύρους να είναι σίγουρος ότι η απόσταση μεταξύ αυτού και του κουνελιού είναι το πολύ
γύρους να είναι σίγουρος ότι η απόσταση μεταξύ αυτού και του κουνελιού είναι το πολύ  ;
;
Ένας κυνηγός και ένα αόρατο κουνέλι παίζουν ένα παιγνίδι στο Ευκλείδειο επίπεδο. Το σημείο εκκίνησης
 του κουνελιού και το σημείο εκκίνησης
του κουνελιού και το σημείο εκκίνησης  του κυνηγού είναι τα ίδια. Μετά από
του κυνηγού είναι τα ίδια. Μετά από  γύρους του παιγνιδιού, το κουνέλι βρίσκεται στο σημείο
γύρους του παιγνιδιού, το κουνέλι βρίσκεται στο σημείο  και ο κυνηγός στο σημείο
και ο κυνηγός στο σημείο  . Στον
. Στον  -οστό γύρο του παιγνιδιού, τρία πράγματα συμβαίνουν κατά σειρά:
-οστό γύρο του παιγνιδιού, τρία πράγματα συμβαίνουν κατά σειρά: (α) Το κουνέλι κινείται αόρατα σε ένα σημείο
 τέτοιο ώστε η απόσταση μεταξύ των σημείων
τέτοιο ώστε η απόσταση μεταξύ των σημείων  και
και  να είναι ακριβώς ίση με
να είναι ακριβώς ίση με  .
.(β) Μια συσκευή παρακολούθησης αναφέρει ένα σημείο
 στον κυνηγό. Η μόνη εγγυημένη πληροφορία είναι ότι η απόσταση μεταξύ των σημείων
στον κυνηγό. Η μόνη εγγυημένη πληροφορία είναι ότι η απόσταση μεταξύ των σημείων  και
και  είναι το πολύ
είναι το πολύ  .
.(γ) Ο κυνηγός κινείται ορατά σε ένα σημείο
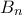 τέτοιο ώστε η απόσταση μεταξύ των σημείων
τέτοιο ώστε η απόσταση μεταξύ των σημείων  και
και 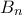 να είναι ακριβώς ίση με
να είναι ακριβώς ίση με  .
.Είναι πάντοτε δυνατόν, ανεξάρτητα από το πως κινείται το κουνέλι και ανεξάρτητα από το ποια σημεία αναφέρονται από την συσκευή παρακολούθησης , για τον κυνηγό να επιλέξει τις κινήσεις του έτσι ώστε μετά από
 γύρους να είναι σίγουρος ότι η απόσταση μεταξύ αυτού και του κουνελιού είναι το πολύ
γύρους να είναι σίγουρος ότι η απόσταση μεταξύ αυτού και του κουνελιού είναι το πολύ  ;
;-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: IMO 2017
Η απάντηση στο πρόβλημα 1 είναι:
 . Θα ανεβάσω την λύση μου σε λίγο.
. Θα ανεβάσω την λύση μου σε λίγο.
 . Θα ανεβάσω την λύση μου σε λίγο.
. Θα ανεβάσω την λύση μου σε λίγο.Γιάννης Μπορμπαντωνάκης
Re: IMO 2017
Να σε βγάλω από τον κόπο (Γιάννης Μπόρμπας έγραψε:Η απάντηση στο πρόβλημα 1 είναι:
. Θα ανεβάσω την λύση μου σε λίγο.
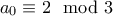 αφού δεν έχω ολοκληρωμένη λύση παρά μόνο μερικά πορίσματα. Η άσκηση ουσιαστικά ξετυλίγεται μέσα από τις απλές δοκιμές.
αφού δεν έχω ολοκληρωμένη λύση παρά μόνο μερικά πορίσματα. Η άσκηση ουσιαστικά ξετυλίγεται μέσα από τις απλές δοκιμές.Λοιπόν, έχουμε:
 αφού κανένα τέλειο τετράγωνο δεν αφήνει υπόλοιπο
αφού κανένα τέλειο τετράγωνο δεν αφήνει υπόλοιπο  . Πάλι έχουμε ότι
. Πάλι έχουμε ότι  για τον ίδιο λόγο.
για τον ίδιο λόγο. Συνεχίζοντας βλέπουμε ότι η ακολουθία λοιπόν είναι γνησίως αύξουσα άρα είναι αδύνατον να ισχύει
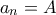 για άπειρα
για άπειρα  .
.Η συνέχεια δική σου...
Re: IMO 2017
Κάποιες λύσεις για το 2 υπάρχουν εδώ https://artofproblemsolving.com/communi ... _problem_2ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Το πρόβλημα 2 είναι
Να βρεθούν όλες οι
που ικανοποιούν την
Κωνσταντίνος Μεταξάς
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: IMO 2017
Πρόβλημα 1
Το πρόβλημα είναι ισοδύναμο με το εξής:
Αρχικά έχουμε έναν ακέραιο . Μπορούμε να κάνουμε τις εξής κινήσεις:
. Μπορούμε να κάνουμε τις εξής κινήσεις:
Κίνηση 1: Αν ο είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον
είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον  .
.
Κίνηση 2Αν ο δεν είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον
δεν είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον  .
.
Για ποιους θετικούς ακέραιους υπάρχει ακέραιος
υπάρχει ακέραιος  τέτοιος ώστε σε οποιαδήποτε κίνηση ο αριθμός που υπάρχει στον πίνακα είναι μικρότερος
τέτοιος ώστε σε οποιαδήποτε κίνηση ο αριθμός που υπάρχει στον πίνακα είναι μικρότερος
ή ίσος του ;
;
Λήμμα 1
Αν κάποια στιγμή ο αριθμός που υπάρχει στον πίνακα (έστω ) αφήνει υπόλοιπο
) αφήνει υπόλοιπο  διαιρούμενος με το
διαιρούμενος με το  τότε ο αριθμός
τότε ο αριθμός  δεν είναι λύση.
δεν είναι λύση.
Απόδειξη
Ας υποθέσουμε ότι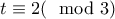 . Τότε αφού το
. Τότε αφού το  δεν είναι τετραγωνικό κατάλοιπο
δεν είναι τετραγωνικό κατάλοιπο  μπορούμε να εκτελούμε διαδοχικά μόνο
μπορούμε να εκτελούμε διαδοχικά μόνο
την δεύτερη κίνηση. Όμως κάθε αριθμός που προκύπτει αφήνει υπόλοιπο διαιρούμενος με το
διαιρούμενος με το  , οπότε εκτελώντας συνεχώς την δεύτερη
, οπότε εκτελώντας συνεχώς την δεύτερη
κίνηση δεν μπορούμε να βρούμε ακέραιο καθώς ο αριθμός που υπάρχει στον πίνακα, συνεχώς μεγαλώνει.
καθώς ο αριθμός που υπάρχει στον πίνακα, συνεχώς μεγαλώνει.
Στην συνέχεια θα δείξουμε επαγωγικά πως:
Αν οι αριθμοί: αποτελούν λύση, τότε και ο
αποτελούν λύση, τότε και ο  αποτελεί λύση.
αποτελεί λύση.
Φυσικά για ο αριθμός
ο αριθμός  είναι λύση διότι οι κινήσεις είναι οι εξής:
είναι λύση διότι οι κινήσεις είναι οι εξής:  οπότε για
οπότε για  έχουμε λύση.
έχουμε λύση.
Στην συνέχεια λαμβάνουμε 2 περιπτώσεις:
(1) Αν ο αριθμός δεν είναι τέλειο τετράγωνο: Τότε μέσω της δεύτερης κίνησης προκύπτει ο
δεν είναι τέλειο τετράγωνο: Τότε μέσω της δεύτερης κίνησης προκύπτει ο  και αφού ο αριθμός
και αφού ο αριθμός  είναι λύση τότε
είναι λύση τότε
φυσικά και ο πρέπει να είναι αναγκαστικά.
πρέπει να είναι αναγκαστικά.
(2) Αν ο αριθμός είναι τέλειο τετράγωνο: Έστω
είναι τέλειο τετράγωνο: Έστω  . σε οποιαδήποτε κίνηση ο αριθμός που προκύπτει διαιρείται με το
. σε οποιαδήποτε κίνηση ο αριθμός που προκύπτει διαιρείται με το  , οπότε
, οπότε
το αμέσως επόμενο τέλειο τετράγωνο μετά το το οποίο είναι πολλαπλάσιο του
το οποίο είναι πολλαπλάσιο του  είναι το
είναι το 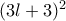 . Αφού όμως
. Αφού όμως 
τότε οι κινήσεις είναι οι εξής: . Όμως
. Όμως 
οπότε ο αριθμός αποτελεί λύση λόγω της υπόθεσης, άρα και ο
αποτελεί λύση λόγω της υπόθεσης, άρα και ο  είναι λύση.
είναι λύση.
Οπότε προκύπτει η λύση: .
.
Επαγωγικά θα δείξουμε πως αν οι αριθμοί δεν είναι λύση τότε και ο
δεν είναι λύση τότε και ο 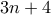 δεν είναι λύση.
δεν είναι λύση.
Για έχουμε ότι:
έχουμε ότι:  , όμως με βάση το λήμμα 1 ο αριθμός
, όμως με βάση το λήμμα 1 ο αριθμός  δεν είναι λύση.
δεν είναι λύση.
Στην συνέχεια λαμβάνουμε τις περιπτώσεις:
(1) Αν ο αριθμός δεν είναι τέλειο τετράγωνο: Όμοια με πριν με βάση την δεύτερη κίνηση προκύπτει ο
δεν είναι τέλειο τετράγωνο: Όμοια με πριν με βάση την δεύτερη κίνηση προκύπτει ο 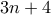 ο οποίος δεν μπορεί να αποτελεί λύση αφού ο
ο οποίος δεν μπορεί να αποτελεί λύση αφού ο  δεν αποτελεί και αυτός.
δεν αποτελεί και αυτός.
(2) Αν ο αριθμός είναι τέλειο τετράγωνο: Λαμβάνουμε 2 υποπεριπτώσεις:
είναι τέλειο τετράγωνο: Λαμβάνουμε 2 υποπεριπτώσεις:
(2.1) Αν . Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του
. Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του  είναι το
είναι το  .
.
Με όμοιο τρόπο οι κινήσεις είναι οι εξής: .
.
Όμως άρα ο αριθμός
άρα ο αριθμός  δεν αποτελεί λύση λόγω της υπόθεσης
δεν αποτελεί λύση λόγω της υπόθεσης
επομένως ούτε και ο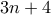 αποτελεί.
αποτελεί.
(2.2) Αν . Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του
. Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του  είναι το
είναι το
 .
.
Πάλι, οι κινήσεις είναι οι εξής: που με βάση το λήμμα 1
που με βάση το λήμμα 1
δεν αποτελεί λύση ο άρα ούτε και ο
άρα ούτε και ο 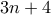 .
.
Ανακεφαλαιώνοντας η αναγκαία και ικανή συνθήκη είναι:
Το πρόβλημα είναι ισοδύναμο με το εξής:
Αρχικά έχουμε έναν ακέραιο
 . Μπορούμε να κάνουμε τις εξής κινήσεις:
. Μπορούμε να κάνουμε τις εξής κινήσεις:Κίνηση 1: Αν ο
 είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον
είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον  .
.Κίνηση 2Αν ο
 δεν είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον
δεν είναι το τετράγωνο ενός ακεραίου, τότε τον σβήνουμε και στην θέση του γράφουμε τον  .
.Για ποιους θετικούς ακέραιους
 υπάρχει ακέραιος
υπάρχει ακέραιος  τέτοιος ώστε σε οποιαδήποτε κίνηση ο αριθμός που υπάρχει στον πίνακα είναι μικρότερος
τέτοιος ώστε σε οποιαδήποτε κίνηση ο αριθμός που υπάρχει στον πίνακα είναι μικρότεροςή ίσος του
 ;
;Λήμμα 1
Αν κάποια στιγμή ο αριθμός που υπάρχει στον πίνακα (έστω
 ) αφήνει υπόλοιπο
) αφήνει υπόλοιπο  διαιρούμενος με το
διαιρούμενος με το  τότε ο αριθμός
τότε ο αριθμός  δεν είναι λύση.
δεν είναι λύση.Απόδειξη
Ας υποθέσουμε ότι
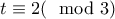 . Τότε αφού το
. Τότε αφού το  δεν είναι τετραγωνικό κατάλοιπο
δεν είναι τετραγωνικό κατάλοιπο  μπορούμε να εκτελούμε διαδοχικά μόνο
μπορούμε να εκτελούμε διαδοχικά μόνοτην δεύτερη κίνηση. Όμως κάθε αριθμός που προκύπτει αφήνει υπόλοιπο
 διαιρούμενος με το
διαιρούμενος με το  , οπότε εκτελώντας συνεχώς την δεύτερη
, οπότε εκτελώντας συνεχώς την δεύτερηκίνηση δεν μπορούμε να βρούμε ακέραιο
 καθώς ο αριθμός που υπάρχει στον πίνακα, συνεχώς μεγαλώνει.
καθώς ο αριθμός που υπάρχει στον πίνακα, συνεχώς μεγαλώνει.Στην συνέχεια θα δείξουμε επαγωγικά πως:
Αν οι αριθμοί:
 αποτελούν λύση, τότε και ο
αποτελούν λύση, τότε και ο  αποτελεί λύση.
αποτελεί λύση.Φυσικά για
 ο αριθμός
ο αριθμός  είναι λύση διότι οι κινήσεις είναι οι εξής:
είναι λύση διότι οι κινήσεις είναι οι εξής:  οπότε για
οπότε για  έχουμε λύση.
έχουμε λύση.Στην συνέχεια λαμβάνουμε 2 περιπτώσεις:
(1) Αν ο αριθμός
 δεν είναι τέλειο τετράγωνο: Τότε μέσω της δεύτερης κίνησης προκύπτει ο
δεν είναι τέλειο τετράγωνο: Τότε μέσω της δεύτερης κίνησης προκύπτει ο  και αφού ο αριθμός
και αφού ο αριθμός  είναι λύση τότε
είναι λύση τότεφυσικά και ο
 πρέπει να είναι αναγκαστικά.
πρέπει να είναι αναγκαστικά.(2) Αν ο αριθμός
 είναι τέλειο τετράγωνο: Έστω
είναι τέλειο τετράγωνο: Έστω  . σε οποιαδήποτε κίνηση ο αριθμός που προκύπτει διαιρείται με το
. σε οποιαδήποτε κίνηση ο αριθμός που προκύπτει διαιρείται με το  , οπότε
, οπότετο αμέσως επόμενο τέλειο τετράγωνο μετά το
 το οποίο είναι πολλαπλάσιο του
το οποίο είναι πολλαπλάσιο του  είναι το
είναι το 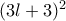 . Αφού όμως
. Αφού όμως 
τότε οι κινήσεις είναι οι εξής:
 . Όμως
. Όμως 
οπότε ο αριθμός
 αποτελεί λύση λόγω της υπόθεσης, άρα και ο
αποτελεί λύση λόγω της υπόθεσης, άρα και ο  είναι λύση.
είναι λύση.Οπότε προκύπτει η λύση:
 .
.Επαγωγικά θα δείξουμε πως αν οι αριθμοί
 δεν είναι λύση τότε και ο
δεν είναι λύση τότε και ο 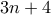 δεν είναι λύση.
δεν είναι λύση.Για
 έχουμε ότι:
έχουμε ότι:  , όμως με βάση το λήμμα 1 ο αριθμός
, όμως με βάση το λήμμα 1 ο αριθμός  δεν είναι λύση.
δεν είναι λύση.Στην συνέχεια λαμβάνουμε τις περιπτώσεις:
(1) Αν ο αριθμός
 δεν είναι τέλειο τετράγωνο: Όμοια με πριν με βάση την δεύτερη κίνηση προκύπτει ο
δεν είναι τέλειο τετράγωνο: Όμοια με πριν με βάση την δεύτερη κίνηση προκύπτει ο 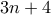 ο οποίος δεν μπορεί να αποτελεί λύση αφού ο
ο οποίος δεν μπορεί να αποτελεί λύση αφού ο  δεν αποτελεί και αυτός.
δεν αποτελεί και αυτός.(2) Αν ο αριθμός
 είναι τέλειο τετράγωνο: Λαμβάνουμε 2 υποπεριπτώσεις:
είναι τέλειο τετράγωνο: Λαμβάνουμε 2 υποπεριπτώσεις:(2.1) Αν
 . Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του
. Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του  είναι το
είναι το  .
.Με όμοιο τρόπο οι κινήσεις είναι οι εξής:
 .
.Όμως
 άρα ο αριθμός
άρα ο αριθμός  δεν αποτελεί λύση λόγω της υπόθεσης
δεν αποτελεί λύση λόγω της υπόθεσης επομένως ούτε και ο
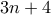 αποτελεί.
αποτελεί.(2.2) Αν
 . Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του
. Τότε το αμέσως επόμενο τέλειο τετράγωνο που δεν είναι πολλαπλάσιο του  είναι το
είναι το  .
.Πάλι, οι κινήσεις είναι οι εξής:
 που με βάση το λήμμα 1
που με βάση το λήμμα 1δεν αποτελεί λύση ο
 άρα ούτε και ο
άρα ούτε και ο 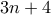 .
.Ανακεφαλαιώνοντας η αναγκαία και ικανή συνθήκη είναι:

Γιάννης Μπορμπαντωνάκης
-
Panagiotis11
- Δημοσιεύσεις: 73
- Εγγραφή: Κυρ Απρ 09, 2017 7:33 pm
- Τοποθεσία: Πάτρα
Re: IMO 2017
Πρόβλημα 4
Έστω και
και  διαφορετικά σημεία ενός κύκλου
διαφορετικά σημεία ενός κύκλου  τέτοια, ώστε το
τέτοια, ώστε το
ευθύγραμμο τμήμα να μην είναι διάμετρός του. Έστω
να μην είναι διάμετρός του. Έστω η εφαπτομένη του
η εφαπτομένη του
κύκλου στο σημείο
στο σημείο  . Σημείο
. Σημείο  είναι τέτοιο, ώστε το
είναι τέτοιο, ώστε το να είναι το μέσον του
να είναι το μέσον του
ευθυγράμμου τμήματος . Στο μικρότερο τόξο
. Στο μικρότερο τόξο  του
του  επιλέγουμε σημείο
επιλέγουμε σημείο  , ώστε
, ώστε
ο περιγεγραμμένος κύκλος του τριγώνου
του τριγώνου  να τέμνει την εφαπτομένη
να τέμνει την εφαπτομένη  σε δύο
σε δύο
διαφορετικά σημεία. Έστω το κοινό σημείο του
το κοινό σημείο του  και της
και της  , που βρίσκεται
, που βρίσκεται
πλησιέστερα στο . H ευθεία
. H ευθεία  τέμνει ξανά τον κύκλο
τέμνει ξανά τον κύκλο  στο σημείο
στο σημείο  . Να
. Να
αποδείξετε ότι η ευθεία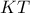 εφάπτεται του κύκλου
εφάπτεται του κύκλου  .
.
Πρόβλημα 5
Δίνεται ακέραιος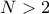 . Ένα σύνολο
. Ένα σύνολο 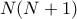 ποδοσφαιριστών,
ποδοσφαιριστών,
μεταξύ των οποίων δεν υπάρχουν δύο με το ίδιο ύψος, στέκονται σε μια γραμμή. Ο
προπονητής θέλει να απομακρύνει ποδοσφαιριστές από αυτή τη
ποδοσφαιριστές από αυτή τη
γραμμή, έτσι ώστε να απομείνει μία νέα γραμμή από ποδοσφαιριστές, στην
ποδοσφαιριστές, στην
οποία να ικανοποιούνται οι ακόλουθες συνθήκες:
συνθήκες:
( ) Κανένας δε στέκεται μεταξύ των δύο πιο ψηλών ποδοσφαιριστών,
) Κανένας δε στέκεται μεταξύ των δύο πιο ψηλών ποδοσφαιριστών,
( ) Κανένας δε στέκεται μεταξύ του τρίτου και τέταρτου ψηλότερων
) Κανένας δε στέκεται μεταξύ του τρίτου και τέταρτου ψηλότερων
ποδοσφαιριστών,
⋮
( ) Κανένας δε στέκεται μεταξύ των δύο πιο κοντών ποδοσφαιριστών.
) Κανένας δε στέκεται μεταξύ των δύο πιο κοντών ποδοσφαιριστών.
Να αποδείξετε ότι αυτό είναι πάντοτε δυνατόν.
Πρόβλημα 6
Ένα διατεταγμένο ζεύγος ακεραίων είναι ένα πρωταρχικό
είναι ένα πρωταρχικό
σημείο, αν ο μέγιστος κοινός διαιρέτης των και
και  είναι
είναι  .Αν
.Αν  είναι ένα
είναι ένα
πεπερασμένο σύνολο πρωταρχικών σημείων, να αποδείξετε ότι υπάρχουν ένας
θετικός ακέραιος και ακέραιοι
και ακέραιοι  τέτοιοι, ώστε για κάθε ζεύγος
τέτοιοι, ώστε για κάθε ζεύγος 
του , να έχουμε:
, να έχουμε:
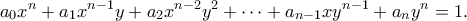
Έστω
 και
και  διαφορετικά σημεία ενός κύκλου
διαφορετικά σημεία ενός κύκλου  τέτοια, ώστε το
τέτοια, ώστε τοευθύγραμμο τμήμα
 να μην είναι διάμετρός του. Έστω
να μην είναι διάμετρός του. Έστω η εφαπτομένη του
η εφαπτομένη τουκύκλου
 στο σημείο
στο σημείο  . Σημείο
. Σημείο  είναι τέτοιο, ώστε το
είναι τέτοιο, ώστε το να είναι το μέσον του
να είναι το μέσον τουευθυγράμμου τμήματος
 . Στο μικρότερο τόξο
. Στο μικρότερο τόξο  του
του  επιλέγουμε σημείο
επιλέγουμε σημείο  , ώστε
, ώστεο περιγεγραμμένος κύκλος
 του τριγώνου
του τριγώνου  να τέμνει την εφαπτομένη
να τέμνει την εφαπτομένη  σε δύο
σε δύοδιαφορετικά σημεία. Έστω
 το κοινό σημείο του
το κοινό σημείο του  και της
και της  , που βρίσκεται
, που βρίσκεταιπλησιέστερα στο
 . H ευθεία
. H ευθεία  τέμνει ξανά τον κύκλο
τέμνει ξανά τον κύκλο  στο σημείο
στο σημείο  . Να
. Νααποδείξετε ότι η ευθεία
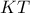 εφάπτεται του κύκλου
εφάπτεται του κύκλου  .
.Πρόβλημα 5
Δίνεται ακέραιος
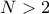 . Ένα σύνολο
. Ένα σύνολο 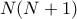 ποδοσφαιριστών,
ποδοσφαιριστών,μεταξύ των οποίων δεν υπάρχουν δύο με το ίδιο ύψος, στέκονται σε μια γραμμή. Ο
προπονητής θέλει να απομακρύνει
 ποδοσφαιριστές από αυτή τη
ποδοσφαιριστές από αυτή τηγραμμή, έτσι ώστε να απομείνει μία νέα γραμμή από
 ποδοσφαιριστές, στην
ποδοσφαιριστές, στηνοποία να ικανοποιούνται οι ακόλουθες
 συνθήκες:
συνθήκες:(
 ) Κανένας δε στέκεται μεταξύ των δύο πιο ψηλών ποδοσφαιριστών,
) Κανένας δε στέκεται μεταξύ των δύο πιο ψηλών ποδοσφαιριστών,(
 ) Κανένας δε στέκεται μεταξύ του τρίτου και τέταρτου ψηλότερων
) Κανένας δε στέκεται μεταξύ του τρίτου και τέταρτου ψηλότερωνποδοσφαιριστών,
⋮
(
 ) Κανένας δε στέκεται μεταξύ των δύο πιο κοντών ποδοσφαιριστών.
) Κανένας δε στέκεται μεταξύ των δύο πιο κοντών ποδοσφαιριστών.Να αποδείξετε ότι αυτό είναι πάντοτε δυνατόν.
Πρόβλημα 6
Ένα διατεταγμένο ζεύγος ακεραίων
 είναι ένα πρωταρχικό
είναι ένα πρωταρχικόσημείο, αν ο μέγιστος κοινός διαιρέτης των
 και
και  είναι
είναι  .Αν
.Αν  είναι ένα
είναι έναπεπερασμένο σύνολο πρωταρχικών σημείων, να αποδείξετε ότι υπάρχουν ένας
θετικός ακέραιος
 και ακέραιοι
και ακέραιοι  τέτοιοι, ώστε για κάθε ζεύγος
τέτοιοι, ώστε για κάθε ζεύγος 
του
 , να έχουμε:
, να έχουμε: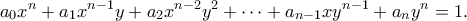
Μπορεί να απογοητευθείς αν αποτύχεις, αλλά είσαι χαμένος αν δεν προσπαθήσεις.
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: IMO 2017
Τελικά το πρόβλημα 3 αποδείχθηκε (όπως περίμενα) το πιο δύσκολο πρόβλημα στην φετινή IMO.
Γιάννης Μπορμπαντωνάκης
Re: IMO 2017
Θα βάλω πλήρη λύση και σχήμα αύριο λόγω της ώρας.Panagiotis11 έγραψε:Πρόβλημα 4
Έστωκαι
διαφορετικά σημεία ενός κύκλου
τέτοια, ώστε το
ευθύγραμμο τμήμανα μην είναι διάμετρός του. Έστω
η εφαπτομένη του
κύκλουστο σημείο
. Σημείο
είναι τέτοιο, ώστε το
να είναι το μέσον του
ευθυγράμμου τμήματος. Στο μικρότερο τόξο
του
επιλέγουμε σημείο
, ώστε
ο περιγεγραμμένος κύκλοςτου τριγώνου
να τέμνει την εφαπτομένη
σε δύο
διαφορετικά σημεία. Έστωτο κοινό σημείο του
και της
, που βρίσκεται
πλησιέστερα στο. H ευθεία
τέμνει ξανά τον κύκλο
στο σημείο
. Να
αποδείξετε ότι η ευθείαεφάπτεται του κύκλου
.
•

• Αφού έχουμε το μεσο ενός τμήματος θα θεωρήσουμε το συμμετρικό του
 ως προς το
ως προς το  ,
,  . Τότε το
. Τότε το  είναι παραλληλόγραμμο άρα
είναι παραλληλόγραμμο άρα  συνεπώς τα
συνεπώς τα  είναι συνευθειακά
είναι συνευθειακά• Το
 είναι εγγράψιμο και εύκολα έπεται το ζητούμενο,
είναι εγγράψιμο και εύκολα έπεται το ζητούμενο,- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: IMO 2017
Καλό! Έχω μια σύντομη απόδειξη αλλά νομίζω ότι είναι δύσκολο πρόβλημα. Δηλαδή αρκετά κατάλληλο για πρόβλημα 5.Panagiotis11 έγραψε: Πρόβλημα 5
Δίνεται ακέραιος. Ένα σύνολο
ποδοσφαιριστών,
μεταξύ των οποίων δεν υπάρχουν δύο με το ίδιο ύψος, στέκονται σε μια γραμμή. Ο
προπονητής θέλει να απομακρύνειποδοσφαιριστές από αυτή τη
γραμμή, έτσι ώστε να απομείνει μία νέα γραμμή απόποδοσφαιριστές, στην
οποία να ικανοποιούνται οι ακόλουθεςσυνθήκες:
() Κανένας δε στέκεται μεταξύ των δύο πιο ψηλών ποδοσφαιριστών,
() Κανένας δε στέκεται μεταξύ του τρίτου και τέταρτου ψηλότερων
ποδοσφαιριστών,
⋮
() Κανένας δε στέκεται μεταξύ των δύο πιο κοντών ποδοσφαιριστών.
Να αποδείξετε ότι αυτό είναι πάντοτε δυνατόν.
Θα αποδείξω επαγωγικά κάτι ισχυρότερο.
Χωρίζω τους
 ποδοσφαιριστές σε
ποδοσφαιριστές σε  ομάδες των
ομάδες των 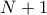 ατόμων. Θα δείξω ότι μπορώ να επιτύχω το ζητούμενο παίρνοντας δύο ποδοσφαιριστές από κάθε ομάδα.
ατόμων. Θα δείξω ότι μπορώ να επιτύχω το ζητούμενο παίρνοντας δύο ποδοσφαιριστές από κάθε ομάδα.Η περίπτωση
 είναι άμεση.
είναι άμεση.Τώρα, ξεκινώντας από τον ψηλότερο, ένας ένας από κάθε ομάδα κάνει ένα βήμα μπροστά. Αυτό συνεχίζεται μέχρι δύο άτομα από κάποια ομάδα να κάνουν ένα βήμα μπροστά. Παίρνω αυτούς τους δύο από αυτήν την ομάδα. Διώχνω όλους τους υπόλοιπους παίκτες της ομάδας. Διώχνω επίσης όσους παίκτες έχουν κάνει βήμα μπροστά. Τώρα μου έμειναν
 ομάδες από
ομάδες από  ποδοσφαριστές, όλοι χαμηλότεροι από τους δύο που επέλεξα. Από την επαγωγική υπόθεση μπορώ να επιλέξω τα υπόλοιπα
ποδοσφαριστές, όλοι χαμηλότεροι από τους δύο που επέλεξα. Από την επαγωγική υπόθεση μπορώ να επιλέξω τα υπόλοιπα  ζεύγη.
ζεύγη.- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: IMO 2017
ΈστωPanagiotis11 έγραψε:Πρόβλημα 4
Έστωκαι
διαφορετικά σημεία ενός κύκλου
τέτοια, ώστε το
ευθύγραμμο τμήμανα μην είναι διάμετρός του. Έστω
η εφαπτομένη του
κύκλουστο σημείο
. Σημείο
είναι τέτοιο, ώστε το
να είναι το μέσον του
ευθυγράμμου τμήματος. Στο μικρότερο τόξο
του
επιλέγουμε σημείο
, ώστε
ο περιγεγραμμένος κύκλοςτου τριγώνου
να τέμνει την εφαπτομένη
σε δύο
διαφορετικά σημεία. Έστωτο κοινό σημείο του
και της
, που βρίσκεται
πλησιέστερα στο. H ευθεία
τέμνει ξανά τον κύκλο
στο σημείο
. Να
αποδείξετε ότι η ευθείαεφάπτεται του κύκλου
.
 .
.Θα δείξουμε πρώτα πως
 .
.Είναι
 .
.Έτσι, τα τρίγωνα
 έχουν
έχουν 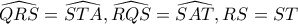 , οπότε είναι ίσα (έμμεσο κριτήριο).
, οπότε είναι ίσα (έμμεσο κριτήριο).Έτσι,
 παραλληλόγραμμο.
παραλληλόγραμμο.Επίσης,
 εγγράψιμο.
εγγράψιμο.Οπότε,
 , και το ζητούμενο γίνεται άμεσο.
, και το ζητούμενο γίνεται άμεσο. Κερδίζουμε ό,τι τολμούμε!
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: IMO 2017
Πολύ καλό πρόβλημα!Panagiotis11 έγραψε: Πρόβλημα 6
Ένα διατεταγμένο ζεύγος ακεραίωνείναι ένα πρωταρχικό
σημείο, αν ο μέγιστος κοινός διαιρέτης τωνκαι
είναι
.Αν
είναι ένα
πεπερασμένο σύνολο πρωταρχικών σημείων, να αποδείξετε ότι υπάρχουν ένας
θετικός ακέραιοςκαι ακέραιοι
τέτοιοι, ώστε για κάθε ζεύγος
του, να έχουμε:
Θα αποδείξουμε με ισχυρή επαγωγή την ύπαρξη ομογενοποιημένου πολυωνύμου ως προς το πλήθος των πρωταρχικών σημείων.
Αν
 και
και  τότε μπορούμε να βρούμε
τότε μπορούμε να βρούμε  τέτοια ώστε
τέτοια ώστε  . Οπότε επιλέγοντας
. Οπότε επιλέγοντας  καταλήγουμε στο ζητούμενο.
καταλήγουμε στο ζητούμενο.Αν υπάρχει πολυώνυμο ομογενοποιημένο πολυώνυμο
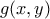 τέτοιο ώστε
τέτοιο ώστε  με
με  να είναι
να είναιπρωταρχικό σημείο
 αρκεί να βρούμε ένα πολυώνυμο
αρκεί να βρούμε ένα πολυώνυμο  τέτοιο ώστε
τέτοιο ώστε 
όπου
 είναι το καινούργιο πρωταρχικό σημείο που προσθέτουμε στο
είναι το καινούργιο πρωταρχικό σημείο που προσθέτουμε στο  .
.Βήμα 1
Αφού
 τότε μπορούμε να βρούμε
τότε μπορούμε να βρούμε  τέτοια ώστε
τέτοια ώστε  . Μπορούμε να αξιοποιήσουμε το παραπάνω
. Μπορούμε να αξιοποιήσουμε το παραπάνωθεωρώντας το πολυώνυμο
 το οποίο μπορεί να πάρει οποιαδήποτε τιμή
το οποίο μπορεί να πάρει οποιαδήποτε τιμή  θελήσουμε την οποία μαζί με το
θελήσουμε την οποία μαζί με το θα την προσδιορίσουμε αργότερα.
θα την προσδιορίσουμε αργότερα.Βήμα 2
Με όμοιο τρόπο παρατηρούμε ότι
 οπότε μπορούμε να χρησιμοποιήσουμε το πολυώνυμο
οπότε μπορούμε να χρησιμοποιήσουμε το πολυώνυμο  για κάποιο
για κάποιο που θα προσδιορίσουμε αργότερα, στην κατασκευή του
που θα προσδιορίσουμε αργότερα, στην κατασκευή του  .
.Βήμα 3
Παίρνουμε
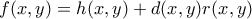 . Αφού
. Αφού  επιλέγουμε
επιλέγουμε .
.Οπότε έχουμε:
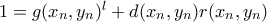
Βήμα 4
Έπειτα παρατηρούμε ότι αν
 (1)για κάποιο
(1)για κάποιο  τότε θα είχαμε:
τότε θα είχαμε:Έστω

 .
. .
. οπότε θα είχαμε
οπότε θα είχαμε 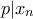 . Με όμοιο τρόπο δείχνουμε ότι
. Με όμοιο τρόπο δείχνουμε ότι  που είναι άτοπο αφού
που είναι άτοπο αφού .
.Βήμα 5
Από το βήμα 4 γνωρίζουμε ότι:
 οπότε μπορούμε να επιλέξουμε
οπότε μπορούμε να επιλέξουμε  για να εξασφαλίσουμε την ακεραιότητα του
για να εξασφαλίσουμε την ακεραιότητα του 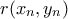 .
.Βήμα 6
Έπειτα, πρέπει να εξισώσουμε τους βαθμούς των πολυωνύμων.
Θέλουμε
 .
.Οπότε επιλέγουμε
 .
.Βήμα 7
Τέλος επειδή εμείς χειριζόμαστε την τιμή του
 επιλέγουμε
επιλέγουμε 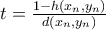 .
.Και έτσι εξασφαλίζουμε την ύπαρξη του
 .
.Γιάννης Μπορμπαντωνάκης
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: IMO 2017
Προτού βάλω την λύση μου, αλλά και ενδιάμεσα της λύσης, βάζω κάποια σχόλια. Δεν χρειάζονται για την απόδειξη αλλά πιστεύω βοηθούν αρκετά στην κατανόηση και στον τρόπο σκέψης για να καταλήξουμε στην λύση.Demetres έγραψε:Πρόβλημα 3
Ένας κυνηγός και ένα αόρατο κουνέλι παίζουν ένα παιγνίδι στο Ευκλείδειο επίπεδο. Το σημείο εκκίνησηςτου κουνελιού και το σημείο εκκίνησης
του κυνηγού είναι τα ίδια. Μετά από
γύρους του παιγνιδιού, το κουνέλι βρίσκεται στο σημείο
και ο κυνηγός στο σημείο
. Στον
-οστό γύρο του παιγνιδιού, τρία πράγματα συμβαίνουν κατά σειρά:
(α) Το κουνέλι κινείται αόρατα σε ένα σημείοτέτοιο ώστε η απόσταση μεταξύ των σημείων
και
να είναι ακριβώς ίση με
.
(β) Μια συσκευή παρακολούθησης αναφέρει ένα σημείοστον κυνηγό. Η μόνη εγγυημένη πληροφορία είναι ότι η απόσταση μεταξύ των σημείων
και
είναι το πολύ
.
(γ) Ο κυνηγός κινείται ορατά σε ένα σημείοτέτοιο ώστε η απόσταση μεταξύ των σημείων
και
να είναι ακριβώς ίση με
.
Είναι πάντοτε δυνατόν, ανεξάρτητα από το πως κινείται το κουνέλι και ανεξάρτητα από το ποια σημεία αναφέρονται από την συσκευή παρακολούθησης , για τον κυνηγό να επιλέξει τις κινήσεις του έτσι ώστε μετά απόγύρους να είναι σίγουρος ότι η απόσταση μεταξύ αυτού και του κουνελιού είναι το πολύ
;
Σχόλιο 1: Η προφανής στρατηγική του κυνηγού είναι να κινείται προς τα
 . Αν δείξουμε πως η απόσταση
. Αν δείξουμε πως η απόσταση  του κυνηγού από τα
του κυνηγού από τα  είναι πάντα το πολύ
είναι πάντα το πολύ  , τότε η απόσταση από τον λαγό είναι πάντα το πολύ
, τότε η απόσταση από τον λαγό είναι πάντα το πολύ  . Δεν είναι δύσκολο να δείξουμε ότι σε κάθε βήμα το
. Δεν είναι δύσκολο να δείξουμε ότι σε κάθε βήμα το  μπορεί να αυξηθεί το πολύ κατά 2. Αυτό ασφαλώς δεν μας κάνει. Όσο όμως πιο κοντά στο
μπορεί να αυξηθεί το πολύ κατά 2. Αυτό ασφαλώς δεν μας κάνει. Όσο όμως πιο κοντά στο  είναι η αύξηση, τόσες περισσότερες πληροφορίες έχουμε για την ακριβή θέση του λαγού, κάτι που επιτρέπει στο επόμενο βήμα τουλάχιστον είτε να μειώσουμε το
είναι η αύξηση, τόσες περισσότερες πληροφορίες έχουμε για την ακριβή θέση του λαγού, κάτι που επιτρέπει στο επόμενο βήμα τουλάχιστον είτε να μειώσουμε το  είτε να αυξηθεί ελάχιστα. Για να δείξουμε ότι τέτοια στρατηγική δουλεύει, πιθανώς με κάποιες τροποποιήσεις, θα πρέπει να λαμβάνουμε υπόψη περισσότερο τις πληροφορίες που παίρνουμε από τις διαδοχικές θέσεις των
είτε να αυξηθεί ελάχιστα. Για να δείξουμε ότι τέτοια στρατηγική δουλεύει, πιθανώς με κάποιες τροποποιήσεις, θα πρέπει να λαμβάνουμε υπόψη περισσότερο τις πληροφορίες που παίρνουμε από τις διαδοχικές θέσεις των  .
. Σχόλιο 2: Πως μπορούμε να δείξουμε ότι ο λαγός αποτυγχάνει; Μια «αφελής» στρατηγική για τον λαγό της μορφής «αν ο κυνηγός είναι εκεί, τότε θα κινηθώ έτσι» είναι καταδικασμένη να αποτύχει. Και αυτό διότι ο κυνηγός μπορεί να είναι τυχεράκιας και να κινείται πάντα προς τον λαγό. Ο μόνος τρόπος για να αποφύγουμε κάτι τέτοιο είναι να έχουμε πολλούς λαγούς! Σε κάθε στιγμή της διαδικασίας μπορεί να έχουμε πολλούς, ίσως και άπειρους λαγούς, οι οποίοι θα ικανοποιούν ότι με βάση το προηγούμενο ιστορικό μπορούν όντως να βρίσκονται σε συγκεκριμένη θέση. Μπορούμε στο τέλος να επιλέξουμε ποιος είναι ο πραγματικός λαγός και ποιοι οι ψεύτικοι.
Σχόλιο 3: Ο κυνηγός μπορεί επίσης να είναι τυχεράκιας και σε σχέση με το τι εμφανίζει η συσκευή παρακολούθησης. Μπορεί π.χ. να έχει εσωτερική πληροφόρηση ότι πάντα η συσκευή δίνει απόσταση 1 βόρεια του λαγού. Για να αποτρέψουμε κάτι τέτοιο θα ελέγχουμε πλήρως εμείς την συσκευή.
Σχόλιο 4: Συνοψίζοντας μια καλή στρατηγική για το κουνέλι θα είναι η εξής: Πρώτα ανακοινώνουμε την ένδειξη της συσκευής. Μετά τοποθετούμε άπειρους λαγούς στις θέσεις που είναι δυνατόν να εμφανίζονται σε σχέση και με το προηγούμενο ιστορικό. Μετά κινείται ο κυνηγός. Τέλος αποφασίζουμε ποιος από τους άπειρους λαγούς είναι ο πραγματικός και συνεχίζουμε.
Πριν το επόμενο σχόλιο, ξεκινώ εισάγοντας κάποιους συμβολισμούς. Γράφω
 για την απόσταση του κυνηγού από το κουνέλι μετά από
για την απόσταση του κυνηγού από το κουνέλι μετά από  γύρους. Αρχικά
γύρους. Αρχικά  . Στον πρώτο γύρο, ανακοινώνουμε το σημείο
. Στον πρώτο γύρο, ανακοινώνουμε το σημείο  . Όπου και αν μετακινηθεί ο κυνηγός, εμείς ως κουνέλι μετακινούμαστε στο αντιδιαμετρικό του σημείο πάνω στον κύκλος ακτίνας
. Όπου και αν μετακινηθεί ο κυνηγός, εμείς ως κουνέλι μετακινούμαστε στο αντιδιαμετρικό του σημείο πάνω στον κύκλος ακτίνας  και κέντρο
και κέντρο  . Έτσι έχουμε
. Έτσι έχουμε  .
.Σχόλιο 5: Θα θέλαμε να δείξουμε ότι αν
 , τότε
, τότε 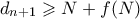 όπου
όπου  είναι μια μικρή αλλά όχι αμελητέα αύξηση. Αν μπορούμε να δείξουμε κάτι τέτοιο τότε είμαστε κοντά στην επίλυση. Αν μάλιστα δεν είναι τόσο καλό το φράγμα αλλά δείξουμε ότι μπορούμε να το πετύχουμε με
είναι μια μικρή αλλά όχι αμελητέα αύξηση. Αν μπορούμε να δείξουμε κάτι τέτοιο τότε είμαστε κοντά στην επίλυση. Αν μάλιστα δεν είναι τόσο καλό το φράγμα αλλά δείξουμε ότι μπορούμε να το πετύχουμε με  κινήσεις τότε ίσως πάρουμε και αρκετές μονάδες. Δυστυχώς κάτι τέτοιο είναι αδύνατο αν
κινήσεις τότε ίσως πάρουμε και αρκετές μονάδες. Δυστυχώς κάτι τέτοιο είναι αδύνατο αν  . Αν π.χ. ο κυνηγός γνωρίζει την ακριβή θέση του λαγού στο προηγούμενο βήμα και κινηθεί προς τον λαγό τότε το
. Αν π.χ. ο κυνηγός γνωρίζει την ακριβή θέση του λαγού στο προηγούμενο βήμα και κινηθεί προς τον λαγό τότε το  δεν μπορεί να αυξηθεί.
δεν μπορεί να αυξηθεί.Η δυσκολία του σχολίου 5 είναι και η σημαντικότερη δυσκολία που πρέπει να παρακαμφθεί. Το κόλπο για να την παρακάμψουμε είναι να δείξουμε ότι
 . Γιατί μπορούμε να το επιτύχουμε αυτό θα το δούμε αργότερα. Προς το παρόν γράφω το σημαντικότερο λήμμα για την λύση της άσκησης:
. Γιατί μπορούμε να το επιτύχουμε αυτό θα το δούμε αργότερα. Προς το παρόν γράφω το σημαντικότερο λήμμα για την λύση της άσκησης:Λήμμα 1: Έστω φυσικός
 . Αν μπορώ να πετύχω
. Αν μπορώ να πετύχω  , τότε μπορώ να πετύχω και
, τότε μπορώ να πετύχω και  .
.Πρωτού αποδείξω το λήμμα, θα δείξω γιατί αυτό είναι αρκετό για την επίλυση της άσκησης.
Λήμμα 2: Έστω φυσικός
 . Αν μπορώ να πετύχω
. Αν μπορώ να πετύχω  , τότε μπορώ να πετύχω και
, τότε μπορώ να πετύχω και  .
.Απόδειξη λήμματος 2: Απλά επαναλαμβάνω το Λήμμα 1 το πολύ
 φορές. Αν σε κάποια φάση πετύχω
φορές. Αν σε κάποια φάση πετύχω  τότε χρησιμοποιώ το Λήμμα 3 πιο κάτω.
τότε χρησιμοποιώ το Λήμμα 3 πιο κάτω.Λήμμα 3: Αν μπορώ να πετύχω
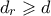 , τότε μπορώ να πετύχω και
, τότε μπορώ να πετύχω και 
Απόδειξη λήμματος 3: Άμεσο αν κινηθώ στην ευθεία που ενώνει τον κυνηγό με το κουνέλι απομακρυνόμενος από τον κυνηγό.
Από το Λήμμα 2 έχουμε
 ,
,  κ.τ.λ. μέχρι το
κ.τ.λ. μέχρι το 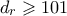 , όπου
, όπου
Άρα μπορώ να πετύχω και
 .
.Μένει να δείξουμε το Λήμμα 1 που είναι και το ζουμί της άσκησης. Πριν την απόδειξη βάζω ακόμη ένα σχόλιο.
Σχόλιο 6: Σε ένα βήμα η τριγωνική ανισότητα δουλεύει εναντίον μας. Για να την κάνουμε να δουλέψει υπέρ μας πρέπει ο κυνηγός να ξεπεράσει το σημείο που βρισκόμασταν στον γύρο
 και μετά να μην γνωρίζει πολλά για το που βρισκόμαστε. Σε αυτήν την περίπτωση η τριγωνική ανισότητα δουλεύει ανάποδα. Ας δούμε και τις τεχνικές λεπτομέρειες:
και μετά να μην γνωρίζει πολλά για το που βρισκόμαστε. Σε αυτήν την περίπτωση η τριγωνική ανισότητα δουλεύει ανάποδα. Ας δούμε και τις τεχνικές λεπτομέρειες:Απόδειξη Λήμματος 1: Χωρίς βλάβη της γενικότητας, ο κυνηγός βρίσκεται στην θέση
 και ο λαγός στην θέση
και ο λαγός στην θέση 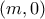 με
με  . Θα υποθέσουμε ακόμη ότι ο λαγός ανακοινώνει πλήρως την θέση του στον κυνηγό. Κλωνοποιούμε τον λαγό σε δύο λαγούς. Για τα επόμενα
. Θα υποθέσουμε ακόμη ότι ο λαγός ανακοινώνει πλήρως την θέση του στον κυνηγό. Κλωνοποιούμε τον λαγό σε δύο λαγούς. Για τα επόμενα  βήματα, ο ένας λαγός κινείται ευθεία προς το σημείο
βήματα, ο ένας λαγός κινείται ευθεία προς το σημείο  και ο άλλος προς το σημείο
και ο άλλος προς το σημείο  . Σε κάθε βήμα ανακοινώνουμε το σημείο
. Σε κάθε βήμα ανακοινώνουμε το σημείο  όπου το
όπου το  είναι η κοινή τετμημένη των δύο λαγών. Στο τέλος των
είναι η κοινή τετμημένη των δύο λαγών. Στο τέλος των  γύρων ο κυνηγός θα βρίσκεται σε ένα σημείο
γύρων ο κυνηγός θα βρίσκεται σε ένα σημείο  με
με  . Οπότε η απόσταση
. Οπότε η απόσταση  του κυνηγού από ένα από τους δύο λαγούς (αυτόν που θα ονομάσουμε πραγματικό) θα ικανοποιεί
του κυνηγού από ένα από τους δύο λαγούς (αυτόν που θα ονομάσουμε πραγματικό) θα ικανοποιεί![\displaystyle{ d^2 = (m + \sqrt{(N+2)^2-1} - x)^2 + 1 \geqslant [(m - (N+2 - \sqrt{(N+2)^2-1})]^2 + 1} \displaystyle{ d^2 = (m + \sqrt{(N+2)^2-1} - x)^2 + 1 \geqslant [(m - (N+2 - \sqrt{(N+2)^2-1})]^2 + 1}](/forum/ext/geomar/texintegr/latexrender/pictures/f4fd72b98e3e88e4e21bf0528cbb2dc6.png)
Αλλά

Οπότε
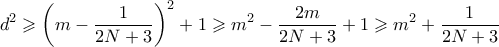
όπως θέλαμε να δείξουμε.
-
simantiris j.
- Δημοσιεύσεις: 246
- Εγγραφή: Σάβ Ιαν 18, 2014 5:07 pm
Re: IMO 2017
Έστω και καθυστερημένα,βρίσκοντας τώρα λίγο χρόνο για να ασχοληθώ,βάζω τη λύση μου για το 2,ώστε να έχουμε λύσεις όλων των προβλημάτων (και ρίχνοντας μια ματιά στο παραπάνω σύνδεσμο δεν υπάρχει ίδια η παρακάτω λύση).
 η δοσμένη πρόταση.Έχουμε:
η δοσμένη πρόταση.Έχουμε:

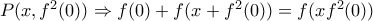 .Έστω
.Έστω 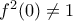 .Τότε σε αυτήν για
.Τότε σε αυτήν για  (η λύση της
(η λύση της  ) έχουμε ότι
) έχουμε ότι  οπότε από αυτή προκύπτει ότι
οπότε από αυτή προκύπτει ότι  που προφανώς είναι λύση.
που προφανώς είναι λύση.
Έστω τώρα .Παρατηρούμε από τη δοσμένη σχέση ότι αν η
.Παρατηρούμε από τη δοσμένη σχέση ότι αν η  είναι λύση της τότε και η
είναι λύση της τότε και η  είναι λύση της,άρα χωρίς βλάβη της γενικότητας υποθέτουμε ότι
είναι λύση της,άρα χωρίς βλάβη της γενικότητας υποθέτουμε ότι  και έχουμε:
και έχουμε:
 (1) άρα
(1) άρα  (2).
(2).
 (3), από όπου εύκολα έχουμε ότι
(3), από όπου εύκολα έχουμε ότι 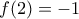 και
και  (και γενικά ότι
(και γενικά ότι  για κάθε ακέραιο
για κάθε ακέραιο  που δε μας ενδιαφέρει εδώ,αλλά μας δείχνει τη συνάρτηση που ψάχνουμε).
που δε μας ενδιαφέρει εδώ,αλλά μας δείχνει τη συνάρτηση που ψάχνουμε).
Επίσης είναι (1 και 3) άρα
(1 και 3) άρα 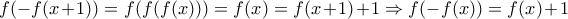 (από 2 και 3).
(από 2 και 3).
 άρα και
άρα και 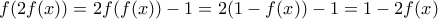 (4).
(4).
 (5),όπου χρησιμοποιήσαμε τις 3 και 4.
(5),όπου χρησιμοποιήσαμε τις 3 και 4.
Τώρα έχουμε 2 επιλογές:Είτε να συνεχίσουμε τη λογική των αντικατάστασεων στην αρχική με την ελπίδα να πάρουμε κάτι καλό,είτε να αρχίσουμε να εξετάζουμε τη σχέση δυο αριθμών με ίδιες εικόνες (υπό μια έννοια το 1-1 της ).Λόγω της (2) θα κινηθούμε προς τη 2η επιλογή.Αξιοποιώντας την (5) και θέλοντας να "σπάσουμε" τη συμμετρία της αρχικής είναι:
).Λόγω της (2) θα κινηθούμε προς τη 2η επιλογή.Αξιοποιώντας την (5) και θέλοντας να "σπάσουμε" τη συμμετρία της αρχικής είναι:
 (6).
(6).
Η (6) είναι σημαντική και πετυχαίνει αυτό που θέλαμε.Πράγματι έστω με
με 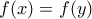 .Εναλλάσοντας τα
.Εναλλάσοντας τα  αυτά στην 6 έχουμε
αυτά στην 6 έχουμε  .Όμως
.Όμως  άρα είναι
άρα είναι  .
.
Από την 5 όμως
Αποδείξαμε λοιπόν ότι αν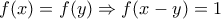 .
.
Επιστρέφοντας λοιπόν στην 2 είναι (7).
(7).
Έχουμε σχεδόν τελειώσει.Πράγματι έστω τέτοιο ώστε
τέτοιο ώστε  .Είναι:
.Είναι:
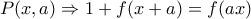 όπου για
όπου για  έχουμε
έχουμε  ,άτοπο.Συνεπώς
,άτοπο.Συνεπώς  .
.
Αυτό για την 7 όμως σημαίνει ότι που επαληθεύει την αρχική.
που επαληθεύει την αρχική.
Άρα όπως εξηγήσαμε οι λύσεις είναι η μηδενική καθώς και οι συναρτήσεις .
.
ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Το πρόβλημα 2 είναι
Να βρεθούν όλες οι
που ικανοποιούν την
 η δοσμένη πρόταση.Έχουμε:
η δοσμένη πρόταση.Έχουμε:
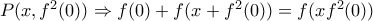 .Έστω
.Έστω 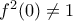 .Τότε σε αυτήν για
.Τότε σε αυτήν για  (η λύση της
(η λύση της  ) έχουμε ότι
) έχουμε ότι  οπότε από αυτή προκύπτει ότι
οπότε από αυτή προκύπτει ότι  που προφανώς είναι λύση.
που προφανώς είναι λύση.Έστω τώρα
 .Παρατηρούμε από τη δοσμένη σχέση ότι αν η
.Παρατηρούμε από τη δοσμένη σχέση ότι αν η  είναι λύση της τότε και η
είναι λύση της τότε και η  είναι λύση της,άρα χωρίς βλάβη της γενικότητας υποθέτουμε ότι
είναι λύση της,άρα χωρίς βλάβη της γενικότητας υποθέτουμε ότι  και έχουμε:
και έχουμε: (1) άρα
(1) άρα  (2).
(2). (3), από όπου εύκολα έχουμε ότι
(3), από όπου εύκολα έχουμε ότι 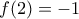 και
και  (και γενικά ότι
(και γενικά ότι  για κάθε ακέραιο
για κάθε ακέραιο  που δε μας ενδιαφέρει εδώ,αλλά μας δείχνει τη συνάρτηση που ψάχνουμε).
που δε μας ενδιαφέρει εδώ,αλλά μας δείχνει τη συνάρτηση που ψάχνουμε).Επίσης είναι
 (1 και 3) άρα
(1 και 3) άρα 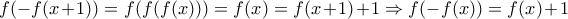 (από 2 και 3).
(από 2 και 3). άρα και
άρα και 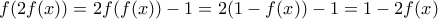 (4).
(4). (5),όπου χρησιμοποιήσαμε τις 3 και 4.
(5),όπου χρησιμοποιήσαμε τις 3 και 4.Τώρα έχουμε 2 επιλογές:Είτε να συνεχίσουμε τη λογική των αντικατάστασεων στην αρχική με την ελπίδα να πάρουμε κάτι καλό,είτε να αρχίσουμε να εξετάζουμε τη σχέση δυο αριθμών με ίδιες εικόνες (υπό μια έννοια το 1-1 της
 ).Λόγω της (2) θα κινηθούμε προς τη 2η επιλογή.Αξιοποιώντας την (5) και θέλοντας να "σπάσουμε" τη συμμετρία της αρχικής είναι:
).Λόγω της (2) θα κινηθούμε προς τη 2η επιλογή.Αξιοποιώντας την (5) και θέλοντας να "σπάσουμε" τη συμμετρία της αρχικής είναι: (6).
(6).Η (6) είναι σημαντική και πετυχαίνει αυτό που θέλαμε.Πράγματι έστω
 με
με 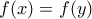 .Εναλλάσοντας τα
.Εναλλάσοντας τα  αυτά στην 6 έχουμε
αυτά στην 6 έχουμε  .Όμως
.Όμως  άρα είναι
άρα είναι  .
.Από την 5 όμως

Αποδείξαμε λοιπόν ότι αν
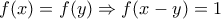 .
.Επιστρέφοντας λοιπόν στην 2 είναι
 (7).
(7).Έχουμε σχεδόν τελειώσει.Πράγματι έστω
 τέτοιο ώστε
τέτοιο ώστε  .Είναι:
.Είναι: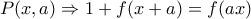 όπου για
όπου για  έχουμε
έχουμε  ,άτοπο.Συνεπώς
,άτοπο.Συνεπώς  .
.Αυτό για την 7 όμως σημαίνει ότι
 που επαληθεύει την αρχική.
που επαληθεύει την αρχική.Άρα όπως εξηγήσαμε οι λύσεις είναι η μηδενική καθώς και οι συναρτήσεις
 .
.Σημαντήρης Γιάννης
Re: IMO 2017
Έχω κάνει ένα αρχείο με τις λύσεις που συζητήθηκαν στην ΙΜΟ. Άλλες είναι των παιδιών, άλλες είναι οι επίσημες, άλλες δικές μου.
Καλή ανάγνωση!
Καλή ανάγνωση!
Σιλουανός Μπραζιτίκος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες


