Σελίδα 1 από 9
ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 9:57 am
από Μπάμπης Στεργίου
Τα θέματα του 2017 !!!
Αναρτήστε τις ωραίες λύσεις και τα σχόλιά σας .
Εύχομαι καλές εμπνύσεις !
Καλά αποτελέσματα στους μαθητές που διαγωνίστηκαν !!!
Μπ
(Δόθηκε οδηγία ότι ο ν είναι φυσικός σε σχετικό θέμα της Β΄Λυκείου)
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 10:15 am
από achilleas
ΘΕΜΑ 2/ Α ΛΥΚΕΙΟΥ
Με συμπλήρωση τετραγώνου παίρνουμε

.
Συνεπώς θέλουμε να βρούμε τους ακεραίους με

Αλλά το 3 δεν είναι τέλειο τετράγωνο, αλλά ούτε άθροισμα δύο τετραγώνων. Γράφεται μοναδικά ως

κι άρα

και

και
 (Σχόλιο*)
(Σχόλιο*)
Συνεπώς,

ή

,

ή

και

Οι λύσεις

, λοιπόν, είναι

,

,

και
 (13 Νοεμβρίου 2017- Σχόλιο*)
(13 Νοεμβρίου 2017- Σχόλιο*)
Αφού

, eίναι

κι άρα

ή

Ομοίως,

ή

και

ή

Ο μοναδικός τρόπος να γράψουμε το 3 ως άθροισμα 0 και 1 είναι

Φιλικά,
Αχιλλέας
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 10:23 am
από achilleas
ΘΕΜΑ 1/ Β ΛΥΚΕΙΟΥ
Είναι

,
οπότε το συμπέρασμα έπεται.
Διαφορετικά, από τη δοθείσα έχουμε

και

Συνεπώς,

και το συμπέρασμα έπεται άμεσα.
Φιλικά,
Αχιλλέας
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 10:31 am
από achilleas
ΘΕΜΑ 3/ Β ΛΥΚΕΙΟΥ
Είναι

οπότε ο

ισούται με

.
Αφού

είναι

και

.
Άρα ο

είναι σύνθετος.
Φιλικά,
Αχιλλέας
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 10:36 am
από george visvikis
Πρόβλημα 2/ Β' Λυκείου

- Θαλής B. Γεωμ. 2017.2.png (20.75 KiB) Προβλήθηκε 15268 φορές
To

είναι ισοσκελές και το

εγγεγραμμένο, άρα:

και


, οπότε τα ισοσκελή τρίγωνα

είναι ίσα, άρα το

είναι ισοσκελές τραπέζιο κι επειδή

θα είναι
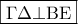
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 10:45 am
από KARKAR

- Γ.png (26.82 KiB) Προβλήθηκε 15254 φορές

,

, ρόμβος αφού οι έγχρωμοι
κύκλοι είναι ίσοι (η κοινή τους χορδή φαίνεται υπό γωνία

)
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:18 am
από achilleas
ΘΕΜΑ 3/ Α ΛΥΚΕΙΟΥ
Ένας αριθμός της δοθείσας μορφής διαιρείται με το 5 αν λήγει σε 5. Τέτοιος αριθμός με ψηφία 4 και 9 δεν μπορεί να σχηματισθεί.
Για να διαιρείται ο αριθμός

με

ή

πρέπει να είναι άρτιος, κι άρα να λήγει σε 4.
Για να διαιρείται με το 3 και το 9 πρέπει το άρθοισμα των ψηφίων του να διαιρείται με το 9.
Αν χρησιμοποιήσουμε το 9, αποκλείεται ο αριθμός να διαιρείται που λήγει σε 4 να διαιρείται με το 9, ούτε με το 3 ούτε με 6.
Συνεπώς, το μέγιστο σύνολο διαιρετών από τη δοθείσα λίστα είναι το

Για να διαρείται με το 8, πρέπει ο αριθμός που σχηματίζεται από τα τελευταία 3 ψηφία να διαιρείται με το 8.
Αφού το

δεν διαιρείται με το 8, όλοι οι άλλοι αριθμοί της μορφής της άσκησης με περισσότερα από 2 ψηφία, δε διαιρούνται με το 8.
Συνεπώς, το μέγιστο σύνολο διαιρετών από τη δοθείσα λίστα είναι το

.
Από τους αριθμούς που διαιρούνται από όσο γίνεται περισσότερους από αυτούς, επιλέγουμε τον ελάχιστο.
Ο πρώτος τέτοιος αριθμός είναι ο

--Σημείωση: Εάν δεν απαιτείται να χρησιμοποιήσουμε το 9 τουλάχιστον μια φορά, τότε η απάντηση είναι 4, όπως αναφέρθηκε από τον Τσιάλα Νικόλαο
εδώ.
Φιλικά,
Αχιλλέας
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:25 am
από george visvikis
Πρόβλημα 4/ A' Λυκείου

- Θαλής A. Γεωμ. 2017.4.png (14.98 KiB) Προβλήθηκε 15196 φορές
Η παραλληλία

και τα ορθογώνια τρίγωνα

, εύκολα δίνουν ότι το

είναι ισόπλευρο.


Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:44 am
από JimNt.
Θέμα 4/Β Λυκείου
Είναι



. Το μήκος της διαγωνίου είναι

. Ισότητα ανν

.
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:46 am
από Τσιαλας Νικολαος
achilleas έγραψε: ↑Σάβ Νοέμ 11, 2017 11:18 am
ΘΕΜΑ 3/ Α ΛΥΚΕΙΟΥ
Ένας αριθμός της δοθείσας μορφής διαιρείται με το 5 αν λήγει σε 5. Αυτοί οι αιρθμοί, όμως, αποκλείουν όλους τους άρτιους διαιρέτες κι έτσι μικραίνουν πολύ το σύνολο των διαιρετών από τους

Για να διαιρείται ο αριθμός

με

ή

πρέπει να είναι άρτιος, κι άρα να λήγει σε 4.
Για να διαιρείται με το 3 και το 9 πρέπει το άρθοισμα των ψηφίων του να διαιρείται με το 9.
Αν χρησιμοποιήσουμε το 9, αποκλείεται ο αριθμός να διαιρείται που λήγει σε 4 να διαιρείται με το 9.
Συνεπώς, το μέγιστο σύνολο διαιρετών από τη δοθείσα λίστα είναι το

.
Για να διαρείται με το 8, πρέπει ο αριθμός που σχηματίζεται από τα τελευταία 3 ψηφία να διαιρείται με το 8.
Αφού το

δεν διαιρείται με το 8, όλοι οι άλλοι αριθμοί της μορφής της άσκησης με περισσότερα από 2 ψηφία, δε διαιρούνται με το 8.
Συνεπώς, το μέγιστο σύνολο διαιρετών από τη δοθείσα λίστα είναι το

.
Από τους αριθμούς που διαιρούνται από όσο γίνεται περισσότερους από αυτούς, επιλέγουμε τον ελάχιστο.
Ο πρώτος τέτοιος αριθμός είναι ο

.
Φιλικά,
Αχιλλέας
Ο ζητούμενος αριθμός ειναι το 994. Το 94 δεν διαιρείτε με το 7
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:47 am
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
Β Λυκείου.
Πρόβλημα 3
έχει παράληψη ότι το

είναι φυσικός.
Σε εξεταστικό κέντρο δόθηκε η πληροφορία στους μαθητές.
Είναι

Αλλά

Ετσι ο αριθμός είναι ο

που είναι σύνθετος γιατί

πρόβλημα 4
Εχουμε ότι

και θέλουμε ελαχιστοποίηση του

Ειναι

Αρα

Αλλά

Η ελάχιστη τιμή της διαγωνίου που είναι

είναι

Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:51 am
από achilleas
Τσιαλας Νικολαος έγραψε: ↑Σάβ Νοέμ 11, 2017 11:46 am
achilleas έγραψε: ↑Σάβ Νοέμ 11, 2017 11:18 am
ΘΕΜΑ 3/ Α ΛΥΚΕΙΟΥ
Ένας αριθμός της δοθείσας μορφής διαιρείται με το 5 αν λήγει σε 5. Αυτοί οι αιρθμοί, όμως, αποκλείουν όλους τους άρτιους διαιρέτες κι έτσι μικραίνουν πολύ το σύνολο των διαιρετών από τους

Για να διαιρείται ο αριθμός

με

ή

πρέπει να είναι άρτιος, κι άρα να λήγει σε 4.
Για να διαιρείται με το 3 και το 9 πρέπει το άρθοισμα των ψηφίων του να διαιρείται με το 9.
Αν χρησιμοποιήσουμε το 9, αποκλείεται ο αριθμός να διαιρείται που λήγει σε 4 να διαιρείται με το 9.
Συνεπώς, το μέγιστο σύνολο διαιρετών από τη δοθείσα λίστα είναι το

.
Για να διαρείται με το 8, πρέπει ο αριθμός που σχηματίζεται από τα τελευταία 3 ψηφία να διαιρείται με το 8.
Αφού το

δεν διαιρείται με το 8, όλοι οι άλλοι αριθμοί της μορφής της άσκησης με περισσότερα από 2 ψηφία, δε διαιρούνται με το 8.
Συνεπώς, το μέγιστο σύνολο διαιρετών από τη δοθείσα λίστα είναι το

.
Από τους αριθμούς που διαιρούνται από όσο γίνεται περισσότερους από αυτούς, επιλέγουμε τον ελάχιστο.
Ο πρώτος τέτοιος αριθμός είναι ο

.
Φιλικά,
Αχιλλέας
Ο ζητούμενος αριθμός ειναι το 994. Το 94 δεν διαιρείτε με το 7
994 είχα στην αρχή αλλά το άλαξα εκ παραδρομής...θα το διορθώσω σύντομα.
Ευχαριστώ!
Αχιλλέας
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:52 am
από ΚΕΦΑΛΟΝΙΤΗΣ
Για το 2ο της Τρίτης Λυκείου...
Η εξίσωση γράφεται ισοδύναμα

,
Oι παράγοντες

και

είναι θετικοί για κάθε x και έτσι η μόνη πραγματική ρίζα είναι το -1.
Συγνώμη για τη βιασύνη , είμαι σε σχολείο για το διαγωνισμό...
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 11:52 am
από achilleas
ΘΕΜΑ 1/Α ΛΥΚΕΙΟΥ
Όχι, διότι ο συνολικός χρόνος παιχνιδιού για όλους τους παίχτες που είναι

λεπτά, δεν διαιρείται με το 16.
Αναλυτικότερα, αλλά όχι στο πνεύμα των διαγωνισμών.
Έστω ότι ο προπονητής χρησιμοποίησε

συνθέσεις για χρόνο

η καθεμία
Τότε

Έστω

ο συνολικός χρόνος του

στου παίκτη κι έστω

ο χρόνος του

στου παίκτη είναι στη σύνθεση

, ο οποίος μπορεί να είναι και μηδέν.
Έχουμε

για

και

για

Για τις

συνθέσεις έχουμε:

Αθροίζοντας κατά γραμμή παίρνουμε

Αθροίζοντας κατά στήλη παίρνουμε

Αφού τα αθοίσματα είναι ίδια έχουμε

Το αριστερό μέλος (το άθροισμα των στοιχείων κατά στήλη στο παρακάτω σχόλιο) είναι πολλαπλάσιο του 16,
ενώ το

, (το άθροισμα των στοιχείων κατά γραμμή) όχι.
Άρα δεν είναι δυνατόν.
Φιλικά,
Αχιλλέας
(Συνεχείς διορθώσεις τυπογραφικών ...

) και προσθήκη πίνακα για καλύτερη επεξήγηση.)
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 12:00 pm
από JimNt.
Διαφορετικά. Αν κάθε παίκτης έπαιξε

λεπτά πρέπει

, που δεν έχει ακέραια λύση.
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 12:04 pm
από JimNt.
Θέμα 1 /Γ Λυκείου
Για

παίρνουμε

. Για

παίρνουμε



. Συνεπώς,

.
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 12:08 pm
από Μιχάλης Τσουρακάκης
Πρόβλημα 1 Β' Λυκείου
Ισχύει


=

Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 12:13 pm
από george visvikis
Το πρόβλημα 1 της Γ' Γυμνασίου είναι σωστό;
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 12:30 pm
από xr.tsif
Θεωρώ ατυχέστατο το πρόβλημα 1 της Α Λυκείου. Επίσης στο 1 της Γ γυμνασίου η αριθμητική τιμή
βγαίνει συναρτήσει του

. πιστεύω ότι ήταν

και ο δεύτερος εκθέτης (τυπο)
Re: ΘΑΛΗΣ 2017
Δημοσιεύτηκε: Σάβ Νοέμ 11, 2017 12:45 pm
από Τσιαλας Νικολαος
 .
.
 κι άρα
κι άρα και
και  και
και 
 ή
ή  ,
, ή
ή 

 , λοιπόν, είναι
, λοιπόν, είναι ,
,  ,
,  και
και 
 , eίναι
, eίναι  κι άρα
κι άρα  ή
ή 
 ή
ή  και
και  ή
ή 
 ,
,



 ισούται με
ισούται με  .
. είναι
είναι  και
και  .
. είναι ισοσκελές και το
είναι ισοσκελές και το  εγγεγραμμένο, άρα:
εγγεγραμμένο, άρα:  και
και 
 , οπότε τα ισοσκελή τρίγωνα
, οπότε τα ισοσκελή τρίγωνα  είναι ίσα, άρα το
είναι ίσα, άρα το  θα είναι
θα είναι 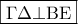
 ,
,  , ρόμβος αφού οι έγχρωμοι
, ρόμβος αφού οι έγχρωμοι )
) ή
ή  πρέπει να είναι άρτιος, κι άρα να λήγει σε 4.
πρέπει να είναι άρτιος, κι άρα να λήγει σε 4. 
 δεν διαιρείται με το 8, όλοι οι άλλοι αριθμοί της μορφής της άσκησης με περισσότερα από 2 ψηφία, δε διαιρούνται με το 8.
δεν διαιρείται με το 8, όλοι οι άλλοι αριθμοί της μορφής της άσκησης με περισσότερα από 2 ψηφία, δε διαιρούνται με το 8. .
.
 και τα ορθογώνια τρίγωνα
και τα ορθογώνια τρίγωνα  , εύκολα δίνουν ότι το
, εύκολα δίνουν ότι το  είναι ισόπλευρο.
είναι ισόπλευρο.



 . Το μήκος της διαγωνίου είναι
. Το μήκος της διαγωνίου είναι  . Ισότητα ανν
. Ισότητα ανν  .
.
 .
. .
. .
. είναι φυσικός.
είναι φυσικός.



 και θέλουμε ελαχιστοποίηση του
και θέλουμε ελαχιστοποίηση του 





 ,
, και
και  είναι θετικοί για κάθε x και έτσι η μόνη πραγματική ρίζα είναι το -1.
είναι θετικοί για κάθε x και έτσι η μόνη πραγματική ρίζα είναι το -1. λεπτά, δεν διαιρείται με το 16.
λεπτά, δεν διαιρείται με το 16. συνθέσεις για χρόνο
συνθέσεις για χρόνο  η καθεμία
η καθεμία
 ο συνολικός χρόνος του
ο συνολικός χρόνος του  στου παίκτη κι έστω
στου παίκτη κι έστω  ο χρόνος του
ο χρόνος του  , ο οποίος μπορεί να είναι και μηδέν.
, ο οποίος μπορεί να είναι και μηδέν.  για
για  και
και  για
για 




 λεπτά πρέπει
λεπτά πρέπει  , που δεν έχει ακέραια λύση.
, που δεν έχει ακέραια λύση. παίρνουμε
παίρνουμε  . Για
. Για  παίρνουμε
παίρνουμε 

 . Συνεπώς,
. Συνεπώς,  .
.


 . πιστεύω ότι ήταν
. πιστεύω ότι ήταν  και ο δεύτερος εκθέτης (τυπο)
και ο δεύτερος εκθέτης (τυπο)