Πρόβλημα 1
Να απλοποιήσετε την παράσταση:
![\displaystyle{A=\sqrt[5]{2\sqrt{5}-3\sqrt{2}}\cdot\sqrt[10]{\dfrac{19+6\sqrt{10}}{2}}} \displaystyle{A=\sqrt[5]{2\sqrt{5}-3\sqrt{2}}\cdot\sqrt[10]{\dfrac{19+6\sqrt{10}}{2}}}](/forum/ext/geomar/texintegr/latexrender/pictures/7973caa4bfc131ed526daa7f66040c80.png)
Πρόβλημα 2
Έστω
 ένας θετικός ακέραιος. Να αποδείξετε ότι:
ένας θετικός ακέραιος. Να αποδείξετε ότι:(α) Το άθροισμα
 των άρτιων αριθμών που βρίσκονται μεταξύ των θετικών ακεραίων
των άρτιων αριθμών που βρίσκονται μεταξύ των θετικών ακεραίων  και
και 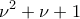 είναι:
είναι: 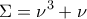
(β) Ο ακέραιος
 διαιρείται με το
διαιρείται με το  .
.Πρόβλημα 3
Θεωρούμε δύο κύκλους
 και
και  , που εφάπτονται εξωτερικά στο
, που εφάπτονται εξωτερικά στο  και φέρουμε τις διαμέτρους τους
και φέρουμε τις διαμέτρους τους  και
και  , αντίστοιχα. Γράφουμε τον κύκλο
, αντίστοιχα. Γράφουμε τον κύκλο  , διαμέτρου
, διαμέτρου  . Έστω
. Έστω  σημείο ενός από τα δύο ημικύκλια, διαμέτρου
σημείο ενός από τα δύο ημικύκλια, διαμέτρου  του κύκλου
του κύκλου  . Η ευθεία
. Η ευθεία  τέμνει τον
τέμνει τον  στο
στο  και τον
και τον  στα σημεία
στα σημεία  , ώστε το
, ώστε το  να βρίσκεται μεταξύ των
να βρίσκεται μεταξύ των  και
και  . Από το κέντρο
. Από το κέντρο  του κύκλου
του κύκλου  φέρουμε την κάθετη στην
φέρουμε την κάθετη στην  , που τέμνει τον κύκλο
, που τέμνει τον κύκλο  στο
στο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
. Πρόβλημα 4
Να προσδιορίσετε όλα τα ζεύγη θετικών και πρώτων ακεραίων
 , για τα οποία ο αριθμός
, για τα οποία ο αριθμός  είναι τέλειο τετράγωνο θετικού ακεραίου.
είναι τέλειο τετράγωνο θετικού ακεραίου.(Ένας θετικός ακέραιος
 είναι τέλειο τετράγωνο θετικού ακεραίου, όταν υπάρχει θετικός ακέραιος
είναι τέλειο τετράγωνο θετικού ακεραίου, όταν υπάρχει θετικός ακέραιος  , ώστε
, ώστε  .)
.)
![\displaystyle A = \sqrt[5]{{2\sqrt 5 - 3\sqrt 2 }} \cdot \sqrt[{10}]{{{{\left( {\frac{{\sqrt {10} + 3}}{{\sqrt 2 }}} \right)}^2}}} = \sqrt[5]{{\left( {2\sqrt 5 - 3\sqrt 2 } \right)\left( {\frac{{\sqrt {10} + 3}}{{\sqrt 2 }}} \right)}} \displaystyle A = \sqrt[5]{{2\sqrt 5 - 3\sqrt 2 }} \cdot \sqrt[{10}]{{{{\left( {\frac{{\sqrt {10} + 3}}{{\sqrt 2 }}} \right)}^2}}} = \sqrt[5]{{\left( {2\sqrt 5 - 3\sqrt 2 } \right)\left( {\frac{{\sqrt {10} + 3}}{{\sqrt 2 }}} \right)}}](/forum/ext/geomar/texintegr/latexrender/pictures/73445587a663b0eeacbdd5af0e9f7b3a.png)
![\displaystyle A = \sqrt[5]{{\frac{{2\sqrt {50} + 6\sqrt 5 - 3\sqrt {20} - 9\sqrt 2 }}{{\sqrt 2 }}}} = \sqrt[5]{{\frac{{10\sqrt 2 + 6\sqrt 5 - 6\sqrt 5 - 9\sqrt 2 }}{{\sqrt 2 }}}} = 1 \displaystyle A = \sqrt[5]{{\frac{{2\sqrt {50} + 6\sqrt 5 - 3\sqrt {20} - 9\sqrt 2 }}{{\sqrt 2 }}}} = \sqrt[5]{{\frac{{10\sqrt 2 + 6\sqrt 5 - 6\sqrt 5 - 9\sqrt 2 }}{{\sqrt 2 }}}} = 1](/forum/ext/geomar/texintegr/latexrender/pictures/918d9b3c7fb0356ebedf89770ce69ef5.png)
 είναι περιττός αφού ο
είναι περιττός αφού ο  είναι άρτιος ,όπως και ο
είναι άρτιος ,όπως και ο  είναι περιττός.
είναι περιττός.
 είναι
είναι 
 , άρα
, άρα 

 , για την οποία η συνάρτηση
, για την οποία η συνάρτηση  με
με  είναι σταθερή.
είναι σταθερή. και
και  η διχοτόμος της. Στην πλευρά
η διχοτόμος της. Στην πλευρά  παίρνουμε τμήμα
παίρνουμε τμήμα  με
με  , στη διχοτόμο
, στη διχοτόμο  με
με  και στην πλευρά
και στην πλευρά 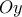 παίρνουμε τμήμα
παίρνουμε τμήμα  με
με  . Αν το σημείο
. Αν το σημείο  είναι το μέσον του
είναι το μέσον του  και
και 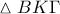 είναι όμοια.
είναι όμοια.  με διαστάσεις
με διαστάσεις  με
με  . Από τις κορυφές
. Από τις κορυφές 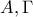 φέρουμε παράλληλες ευθείες
φέρουμε παράλληλες ευθείες  , οι οποίες δεν έχουν άλλο κοινό σημείο με το ορθογώνιο και στη συνέχεια φέρουμε από τις κορυφές
, οι οποίες δεν έχουν άλλο κοινό σημείο με το ορθογώνιο και στη συνέχεια φέρουμε από τις κορυφές  ευθείες
ευθείες  κάθετες στις
κάθετες στις  σχηματίζουν ένα νέο ορθογώνιο
σχηματίζουν ένα νέο ορθογώνιο 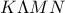 , του οποίου το εμβαδόν συμβολίζουμε με
, του οποίου το εμβαδόν συμβολίζουμε με  . Να βρείτε τη μέγιστη τιμή
. Να βρείτε τη μέγιστη τιμή  του
του 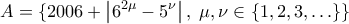 .
.

 είναι πρώτοι, διακρίνουμε τις εξής περιπτώσεις:
είναι πρώτοι, διακρίνουμε τις εξής περιπτώσεις:
 (άτοπο)
(άτοπο)
 (άτοπο)
(άτοπο)
 , άρα
, άρα  (
(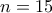 , άτοπο) ή
, άτοπο) ή  και
και  .
. ικανοποιεί την αρχική και εγκρίνεται.
ικανοποιεί την αρχική και εγκρίνεται.
 Θα αποδείξουμε ότι αυτή είναι η ελάχιστη τιμή. Αρκεί να αποκλείσουμε τις τιμές
Θα αποδείξουμε ότι αυτή είναι η ελάχιστη τιμή. Αρκεί να αποκλείσουμε τις τιμές 
 περιττός.
περιττός. λήγει είτε σε
λήγει είτε σε  , είτε σε
, είτε σε  , άρα από τις περιττές περιπτώσεις αρκεί να εξετάσουμε τις
, άρα από τις περιττές περιπτώσεις αρκεί να εξετάσουμε τις 
 .
. άτοπο.
άτοπο. Αυτή πάλι είναι αδύνατη, εξετάζοντας το τελευταίο ψηφίο του αριστερού μέλους.
Αυτή πάλι είναι αδύνατη, εξετάζοντας το τελευταίο ψηφίο του αριστερού μέλους.

 , με τις ιδιότητες:
, με τις ιδιότητες:


 , με
, με  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
. . Οι διχοτόμοι των γωνιών
. Οι διχοτόμοι των γωνιών  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο 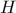 και
και 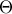 , αντίστοιχα. Έστω
, αντίστοιχα. Έστω  . Η ευθεία
. Η ευθεία  τέμνει τις ευθείες
τέμνει τις ευθείες  και
και  το σημείο τομής των διαγωνίων
το σημείο τομής των διαγωνίων  του
του  τέμνει για δεύτερη φορά τις ευθείες
τέμνει για δεύτερη φορά τις ευθείες  στα σημεία
στα σημεία  και
και  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  βρίσκονται πάνω στον ίδιο κύκλο.
βρίσκονται πάνω στον ίδιο κύκλο. σχηματίζουν ένα νέο ορθογώνιο
σχηματίζουν ένα νέο ορθογώνιο  κι επειδή η
κι επειδή η  είναι διχοτόμος, τα τρίγωνα
είναι διχοτόμος, τα τρίγωνα  είναι όμοια,
είναι όμοια,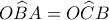 και
και  Αλλά,
Αλλά, 
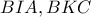 είναι όμοια (έχουν δύο πλευρές ανάλογες και τις περιεχόμενες γωνίες ίσες).
είναι όμοια (έχουν δύο πλευρές ανάλογες και τις περιεχόμενες γωνίες ίσες). θα πρέπει να επαληθεύεται για κάθε τιμή του
θα πρέπει να επαληθεύεται για κάθε τιμή του  άρα θα είναι και
άρα θα είναι και 

 τότε:
τότε:  που εξαρτάται από το
που εξαρτάται από το  τότε:
τότε: 


 η συνάρτηση είναι σταθερή και παίρνει την τιμή
η συνάρτηση είναι σταθερή και παίρνει την τιμή 
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  [1]
[1] για την
για την  με
με 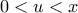 [2]
[2] είναι γν. αύξουσα για
είναι γν. αύξουσα για  διότι
διότι  από [2] αφού
από [2] αφού  και τότε
και τότε ![\displaystyle{[e,\pi]} \displaystyle{[e,\pi]}](/forum/ext/geomar/texintegr/latexrender/pictures/785016f871b3f44f20f2b636620ef9f5.png) μια που είναι και συνεχής στο διάστημα αυτό αρα
μια που είναι και συνεχής στο διάστημα αυτό αρα 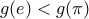 που είναι το ζητούμενο
που είναι το ζητούμενο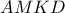 προκύπτει ότι πως
προκύπτει ότι πως 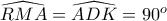 .
. , δηλαδή
, δηλαδή  .
.  είναι ορθογώνιο, το
είναι ορθογώνιο, το  είναι το μέσο του
είναι το μέσο του  .
. (
( ) με έγκεντρο
) με έγκεντρο  . Οι ευθείες
. Οι ευθείες  και
και  τέμνουν τις
τέμνουν τις  και
και  αντίστοιχα στα σημεία
αντίστοιχα στα σημεία  . Να αποδειχθεί ότι η κάθετη από το
. Να αποδειχθεί ότι η κάθετη από το  διέρχεται από το μέσο του
διέρχεται από το μέσο του  .
. , την
, την  και την
και την  .
. με διατέμνουσα την
με διατέμνουσα την  έχουμε την σχέση:
έχουμε την σχέση:
 , οπότε αρκεί:
, οπότε αρκεί:
 με διατέμνουσα την
με διατέμνουσα την  έχουμε την σχέση:
έχουμε την σχέση:

 και
και  έχουν κοινή γωνία, επομένως ο λόγος
έχουν κοινή γωνία, επομένως ο λόγος  δηλώνει το λόγο των εμβαδών τους.
δηλώνει το λόγο των εμβαδών τους. .
. .
. . Θα είναι
. Θα είναι  ,
,  ,
,  και
και  .
. έχουμε πως
έχουμε πως  , ενώ από νόμο ημιτόνων στο τρίγωνο
, ενώ από νόμο ημιτόνων στο τρίγωνο  .
.
 , ενώ
, ενώ  .
.

 ορθογώνιο τρίγωνο και
ορθογώνιο τρίγωνο και  τα ίχνη των διχοτόμων του από τις κορυφές
τα ίχνη των διχοτόμων του από τις κορυφές  αντίστοιχα τότε η ευθεία που ορίζουν το μέσο
αντίστοιχα τότε η ευθεία που ορίζουν το μέσο  και το έγκεντρο
και το έγκεντρο  . Για το δεύτερο μέλος έχουμε από το δεύτερο θεώρημα διαμέσων
. Για το δεύτερο μέλος έχουμε από το δεύτερο θεώρημα διαμέσων![\left.\begin{matrix}
2BO^2+ZE^2/2=BZ^2+BE^2\\
2CO^2+ZE^2/2=CZ^2+CE^2
\end{matrix}\right\} \Rightarrow 2(BO^2-CO^2) = BZ^2+BE^2-CZ^2-CE^2 = \xrightarrow[BE^2=AB^2+AE^2]{CZ^2=AZ^2+AC^2} = \left.\begin{matrix}
2BO^2+ZE^2/2=BZ^2+BE^2\\
2CO^2+ZE^2/2=CZ^2+CE^2
\end{matrix}\right\} \Rightarrow 2(BO^2-CO^2) = BZ^2+BE^2-CZ^2-CE^2 = \xrightarrow[BE^2=AB^2+AE^2]{CZ^2=AZ^2+AC^2} =](/forum/ext/geomar/texintegr/latexrender/pictures/c6b56526963012737e513ee222889a65.png)
 (1)
(1)





 και η παράσταση γίνεται
και η παράσταση γίνεται
 (2)
(2) , όπου
, όπου  ). Ομως
). Ομως  . Οπότε έχουμε
. Οπότε έχουμε
 το κέντρο (
το κέντρο ( θα είναι το μέσο του
θα είναι το μέσο του  . Οπότε σύμφωνα με το παραπάνω λήμμα θα είναι
. Οπότε σύμφωνα με το παραπάνω λήμμα θα είναι  .
. και το τετράπλευρο
και το τετράπλευρο  είναι εγγεγραμμένο θα ισχύει και
είναι εγγεγραμμένο θα ισχύει και  . Από την καθετότητα
. Από την καθετότητα  . Δηλαδή
. Δηλαδή  και τα σημεία
και τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά. το σημείο
το σημείο  είναι το μέσο του τόξου
είναι το μέσο του τόξου  . Άρα το τρίγωνο
. Άρα το τρίγωνο  είναι ισοσκελές με
είναι ισοσκελές με  . Η
. Η  θα είναι ύψος και διχοτόμος, οπότε
θα είναι ύψος και διχοτόμος, οπότε  (1).
(1).  . Επομένως
. Επομένως  και εφόσον
και εφόσον 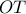 είναι μεσοπαράλληλος των
είναι μεσοπαράλληλος των 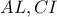 θα διέρχεται και από το μέσο, έστω
θα διέρχεται και από το μέσο, έστω  .
.  είναι διάμεσος και ύψος του τριγώνου
είναι διάμεσος και ύψος του τριγώνου  . Άρα το τρίγωνο αυτό είναι ισοσκελές με
. Άρα το τρίγωνο αυτό είναι ισοσκελές με  και
και  (2).
(2).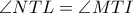 .
.