Πρόβλημα 1. Σε στρογγυλό τραπέζι ανά ίσα διαστήματα είναι τοποθετημένα γλυκά. Ο Γρηγόρης κινείται γύρο από το τραπέζι και τρώει κάθε τρίτο γλυκό που συναντάει (κάθε γλυκό μπορεί να συναντάται αρκετές φορές). Όταν στο τραπέζι δεν έμειναν γλυκά, παρατήρησε, ότι τελευταία πήρε το γλυκό, το οποίο συνάντησε πρώτο και έκανε ακριβώς 7 στροφές γύρω από το τραπέζι. Πόσα ήταν τα γλυκά;
Πρόβλημα 2. Σε τρίγωνο
 , όπου η γωνία
, όπου η γωνία  είναι ορθή και η γωνία
είναι ορθή και η γωνία  μικρότερη της γωνίας
μικρότερη της γωνίας  , φέρουμε την διάμεσο
, φέρουμε την διάμεσο  . Στην πλευρά
. Στην πλευρά  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο, ώστε
τέτοιο, ώστε  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι 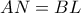 .
.Πρόβλημα 3. Για τους θετικούς αριθμούς
 είναι γνωστό, ότι
είναι γνωστό, ότι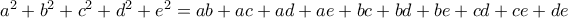 .
.Αποδείξετε, ότι μεταξύ αυτών των αριθμών θα βρεθούν τρεις, τέτοιοι ώστε να μην υπάρχει τρίγωνο με μήκη πλευρών αυτούς τους αριθμούς.
Πρόβλημα 4. Να κόψετε το παρακάτω σχήμα σε δυο ίσα κομμάτια.
Πρόβλημα 5. Θα ονομάσουμε ένα σημείο του επιπέδου «κόμβο», αν και οι δυο συντεταγμένες του είναι ακέραιοι αριθμοί. Δίνεται τρίγωνο με τις κορυφές του σε κόμβους, στο εσωτερικό του οποίου είναι τοποθετημένοι τουλάχιστον δυο κόμβοι. Να αποδείξετε, ότι μεταξύ των κόμβων στο εσωτερικό του τριγώνου μπορούμε να διαλέξουμε τέτοιους δυο, ώστε η ευθεία που διέρχεται από αυτούς περιέχει μια από τις κορυφές του τριγώνου ή είναι παράλληλη προς μία από τις πλευρές του.
Πρόβλημα 6. Εκατό οπαδοί θέλουν να μεταβούν με τρένο 12 βαγονιών από την πρώτη στάση που είναι ο σύνδεσμός τους στην 76η που είναι το γήπεδο. Γνωρίζουν, ότι στην πρώτη στάση σε δυο από τα βαγόνια του τρένου βρίσκονται δυο ελεγκτές. Μετά την τέταρτη στάση σε κάθε επιβίβαση/αποβίβαση ένας από τους ελεγκτές μεταβαίνει σε διπλανό βαγόνι, εξάλλου οι ελεγκτές κινούνται με την σειρά. Ο οπαδός βλέπει τον ελεγκτή, μόνο όταν βρίσκεται σε διπλανό βαγόνι ή σε παραδιπλανό. Σε κάθε στάση κάθε οπαδός μπορεί (προλαβαίνει) να μετεπιβιβαστεί μέσο της πλατφόρμας το πολύ 3 βαγόνια μακρύτερα(για παράδειγμα, από το 7ο βαγόνι ο οπαδός μπορεί να μετεπιβιβαστεί σε οποιοδήποτε βαγόνι από το 4ο μέχρι το 10ο και να κάτσει σε αυτό). Ποιος είναι ο μέγιστος αριθμός οπαδών που δεν θα βρεθεί ούτε μια φορά στο ίδιο βαγόνι με ελεγκτή, με οποιονδήποτε τρόπο και αν κινούνται οι ελεγκτές; (Άλλή πληροφόριση για τους ελεγκτές, πέραν αυτής που αναφέρει το πρόβλημα, οι οπαδοί δεν έχουν. Οι οπαδοί συνεννοούνται για την στρατηγική που θα ακολουθήσουν εκ τον προτέρων).

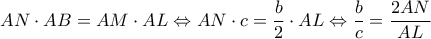


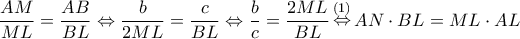

 άρα η
άρα η 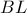 εφάπτεται στον περίκυκλο του
εφάπτεται στον περίκυκλο του  οπότε
οπότε 
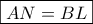
 . Μπορούμε να υποθέσουμε ότι
. Μπορούμε να υποθέσουμε ότι  αφού σε διαφορετική περίπτωση τα μήκη
αφού σε διαφορετική περίπτωση τα μήκη 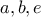 δεν σχηματίζουν τρίγωνο. Τότε:
δεν σχηματίζουν τρίγωνο. Τότε: