Πρώτη μέρα
1. Στο εσωτερικό κυρτού πενταγώνου σημειώθηκε σημείο και ενώθηκε με όλες τις κορυφές του. Ποιος είναι ο μέγιστος αριθμός εκ των δέκα τμημάτων (πέντε πλευρές και τα πέντε τμήματα, που ενώνουν το δοθέν σημείο με τις κορυφές του πενταγώνου) που μπορεί να έχουν μήκος
 ;
;2. Σε κάθε κελί ενός πίνακα
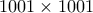 τοποθετήθηκε είτε το
τοποθετήθηκε είτε το  είτε το
είτε το  . Προέκυψε, ότι σε οποιαδήποτε στήλη τα μηδενικά είναι περισσότερα από τις μονάδες. Άραγε οπωσδήποτε θα βρεθούν δυο στήλες τέτοιες, ώστε ο αριθμός των γραμμών, στη τομή των οποίων με αυτές τις στήλες είναι τοποθετημένα μόνο μηδενικά, είναι μεγαλύτερος του αριθμού των γραμμών, στη τομή των οποίων με αυτές τις στήλες είναι τοποθετημένες μόνο μονάδες;
. Προέκυψε, ότι σε οποιαδήποτε στήλη τα μηδενικά είναι περισσότερα από τις μονάδες. Άραγε οπωσδήποτε θα βρεθούν δυο στήλες τέτοιες, ώστε ο αριθμός των γραμμών, στη τομή των οποίων με αυτές τις στήλες είναι τοποθετημένα μόνο μηδενικά, είναι μεγαλύτερος του αριθμού των γραμμών, στη τομή των οποίων με αυτές τις στήλες είναι τοποθετημένες μόνο μονάδες;3. Δίνεται μη ισοσκελές τρίγωνο
 , στο οποίο
, στο οποίο  . Έστω
. Έστω  το μέσο της πλευράς
το μέσο της πλευράς  . Το σημείο
. Το σημείο  είναι το κέντρο του περιγεγραμμένου κύκλου
είναι το κέντρο του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου  . Η χορδή
. Η χορδή  τέμνει σε ένα δεύτερο σημείο
τέμνει σε ένα δεύτερο σημείο  το κύκλο
το κύκλο  . Αποδείξτε, ότι το κέντρο του περιγεγραμμένου κύκλου
. Αποδείξτε, ότι το κέντρο του περιγεγραμμένου κύκλου  του τριγώνου
του τριγώνου 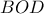 , βρίσκεται επί της ευθείας
, βρίσκεται επί της ευθείας  .
.4. Αρχικά στον πίνακα είναι γραμμένοι οι αριθμοί
 . Κάθε λεπτό όλοι οι αριθμοί
. Κάθε λεπτό όλοι οι αριθμοί  που είναι γραμμένοι στον πίνακα σβήνονται και στη θέση τους γράφονται οι αριθμοί
που είναι γραμμένοι στον πίνακα σβήνονται και στη θέση τους γράφονται οι αριθμοί 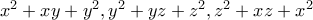 . Μπορεί να προκύψει σε κάποια χρονική στιγμή και οι τρεις αριθμοί στον πίνακα να είναι ρητοί;
. Μπορεί να προκύψει σε κάποια χρονική στιγμή και οι τρεις αριθμοί στον πίνακα να είναι ρητοί;5. Θα ονομάσουμε βάρκα ένα τραπέζιο με βάσεις
 και
και  που προκύπτει αν προσκολλήσουμε στις απέναντι πλευρές ενός μοναδιαίου τετραγώνου δυο τρίγωνα (μισό του τετραγώνου).
Σε ένα τετράγωνο
που προκύπτει αν προσκολλήσουμε στις απέναντι πλευρές ενός μοναδιαίου τετραγώνου δυο τρίγωνα (μισό του τετραγώνου).
Σε ένα τετράγωνο  είναι τοποθετημένη μια αόρατη βάρκα (μπορεί να περιστραφεί, δεν εξέρχεται από το όριο του τετραγώνου, το μεσαίο τετράγωνό της κείται εξ ολοκλήρου σε ένα από τα κελιά του τετραγώνου). Με μια βολή μπορούμε να χρωματίσουμε οποιοδήποτε τριγωνικό μισό ενός κελιού. Αν μια βολή τέμνεται με το εσωτερικό της βάρκας (δηλαδή η τομή του τριγώνου της βολής με την βάρκα έχει μη μηδενικό εμβαδόν), τότε αυτή θεωρείτε βυθισμένη. Ποιος είναι ο ελάχιστος αριθμός βολών που χρειάζονται, ώστε να είμαστε σίγουροι ότι η βάρκα βυθίστηκε;
είναι τοποθετημένη μια αόρατη βάρκα (μπορεί να περιστραφεί, δεν εξέρχεται από το όριο του τετραγώνου, το μεσαίο τετράγωνό της κείται εξ ολοκλήρου σε ένα από τα κελιά του τετραγώνου). Με μια βολή μπορούμε να χρωματίσουμε οποιοδήποτε τριγωνικό μισό ενός κελιού. Αν μια βολή τέμνεται με το εσωτερικό της βάρκας (δηλαδή η τομή του τριγώνου της βολής με την βάρκα έχει μη μηδενικό εμβαδόν), τότε αυτή θεωρείτε βυθισμένη. Ποιος είναι ο ελάχιστος αριθμός βολών που χρειάζονται, ώστε να είμαστε σίγουροι ότι η βάρκα βυθίστηκε;Δεύτερη Μέρα
6. Ο Πέτρος διάλεξε ένα φυσικό αριθμό
 και έγραψε στον πίνακα τα ακόλουθα κλάσματα
και έγραψε στον πίνακα τα ακόλουθα κλάσματα .
.Έστω ότι ο αριθμός
 διαιρείτε με τον φυσικό αριθμό
διαιρείτε με τον φυσικό αριθμό  . Να αποδείξετε, ότι μεταξύ των γραμμένων κλασμάτων θα βρεθεί κλάσμα, ίσο με το αριθμό
. Να αποδείξετε, ότι μεταξύ των γραμμένων κλασμάτων θα βρεθεί κλάσμα, ίσο με το αριθμό  .
.7. Η συνάρτηση
 που ορίζεται σε όλο το σύνολο των πραγματικών αριθμών και για κάθε πραγματικό
που ορίζεται σε όλο το σύνολο των πραγματικών αριθμών και για κάθε πραγματικό  και
και  ικανοποιεί την συνθήκη
ικανοποιεί την συνθήκη  .
.Αληθεύει, ότι η συνάρτηση
 θα είναι οπωσδήποτε άρτια;
θα είναι οπωσδήποτε άρτια;8. Να αποδείξετε, ότι θα βρεθεί τέτοιος φυσικός αριθμός
 , ώστε το άθροισμα όλων των πρώτων αριθμών, μικρότερων του
, ώστε το άθροισμα όλων των πρώτων αριθμών, μικρότερων του  , θα είναι σχετικά πρώτο με τον
, θα είναι σχετικά πρώτο με τον  .
.9. Σε ένα σύνολο
 παιδιών, μερικά παιδιά είναι φίλοι (η φιλία είναι αμοιβαία). Είναι γνωστό, ότι αν αφαιρέσουμε οποιοδήποτε παιδί τα εναπομείναντα
παιδιών, μερικά παιδιά είναι φίλοι (η φιλία είναι αμοιβαία). Είναι γνωστό, ότι αν αφαιρέσουμε οποιοδήποτε παιδί τα εναπομείναντα  παιδιά μπορούμε να τα χωρίσουμε σε
παιδιά μπορούμε να τα χωρίσουμε σε  ομάδες των τριών παιδιών έτσι, ώστε σε κάθε ομάδα και τα τρία παιδιά ανά δυο να είναι φίλοι. Να βρείτε το μικρότερο δυνατό αριθμό ζευγών παιδιών που είναι φίλοι.
ομάδες των τριών παιδιών έτσι, ώστε σε κάθε ομάδα και τα τρία παιδιά ανά δυο να είναι φίλοι. Να βρείτε το μικρότερο δυνατό αριθμό ζευγών παιδιών που είναι φίλοι.10. Στη σφαίρα
 σημειώθηκε σταθερό σημείο
σημειώθηκε σταθερό σημείο  και στη σφαίρα
και στη σφαίρα  σταθερό σημείο
σταθερό σημείο  . Στη σφαίρα
. Στη σφαίρα  διαλέγουμε ένα μεταβλητό σημείο
διαλέγουμε ένα μεταβλητό σημείο  και στη σφαίρα
και στη σφαίρα  μεταβλητό σημείο
μεταβλητό σημείο  έτσι, ώστε
έτσι, ώστε  . Να αποδείξετε, ότι το μέσο όλων των τμημάτων
. Να αποδείξετε, ότι το μέσο όλων των τμημάτων  που κατασκευάζονται με αυτό το τρόπο βρίσκονται σε μια σφαίρα.
που κατασκευάζονται με αυτό το τρόπο βρίσκονται σε μια σφαίρα.
 και έχουμε πως:
και έχουμε πως: , άρα είτε
, άρα είτε  , είτε
, είτε  για κάθε
για κάθε  και προκύπτει ότι:
και προκύπτει ότι: .
. . Ολα τα κλάσματα είναι της μορφής
. Ολα τα κλάσματα είναι της μορφής  ,
,  ακέραιος ώστε
ακέραιος ώστε  . Συνεπώς αφού
. Συνεπώς αφού  θα υπάρχει το κλάσμα
θα υπάρχει το κλάσμα  και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε. το τρίγωνο
το τρίγωνο  είναι ορθογώνιο και ισοσκελές. Έστω
είναι ορθογώνιο και ισοσκελές. Έστω  το κέντρο του κύκλου
το κέντρο του κύκλου 
 η ακτίνα του κύκλου
η ακτίνα του κύκλου  Προφανώς το
Προφανώς το  η οποία διέρχεται από το
η οποία διέρχεται από το 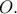

 άρα το
άρα το 
 όπου
όπου  είναι περιττοί ακέραιοι. Στο πρώτο βήμα ισχύει αφού παίρνω τους αριθμούς
είναι περιττοί ακέραιοι. Στο πρώτο βήμα ισχύει αφού παίρνω τους αριθμούς  . Για το επαγωγικό βήμα, αν έχω τους
. Για το επαγωγικό βήμα, αν έχω τους  περιττούς, στο επόμενο βήμα παίρνω τους
περιττούς, στο επόμενο βήμα παίρνω τους  και
και  οι οποίοι είναι της μορφής που ισχυρίζομαι.
οι οποίοι είναι της μορφής που ισχυρίζομαι. στην πρώτη σφαίρα
στην πρώτη σφαίρα 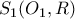 και ένα σταθερό σημείο
και ένα σταθερό σημείο  στη δεύτερη
στη δεύτερη 
 αντίστοιχα στις σφαίρες αυτές
αντίστοιχα στις σφαίρες αυτές  .
. του τμήματος
του τμήματος  .
. προς τη διάκεντρο των σφαιρών
προς τη διάκεντρο των σφαιρών  και πάνω σ' αυτές ορίζουμε αντίστοιχα τα σημεία
και πάνω σ' αυτές ορίζουμε αντίστοιχα τα σημεία  τέτοια ώστε:
τέτοια ώστε: 
 είναι ένα τραπέζιο, δηλαδή:
είναι ένα τραπέζιο, δηλαδή: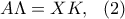
 ανήκει στο μεσοκάθετο επίπεδο του τμήματος
ανήκει στο μεσοκάθετο επίπεδο του τμήματος 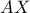 καθώς και του
καθώς και του  , άρα το τραπέζιο
, άρα το τραπέζιο 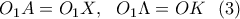
 της διακέντρου
της διακέντρου 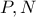 αντίστοιχα
αντίστοιχα  και
και  .
.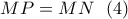
 , φέροντες από τα σημεία
, φέροντες από τα σημεία 


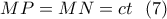
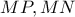 είναι διάμεσοι των τριγώνων αυτών(εύκολα δείχνεται).
είναι διάμεσοι των τριγώνων αυτών(εύκολα δείχνεται).  , όπου
, όπου  το μέσο του σταθερού μήκους
το μέσο του σταθερού μήκους  χρειαζόμαστε τουλάχιστον δύο βολές. Πράγματι αν πυροβολήσουμε μόνο μία βολή και η βολή δεν χτυπήσει στο μεσαίο κελί τότε δεν θα είμαστε σίγουροι ότι βυθίσαμε την βάρκα αφού αυτή μπορεί να βρίσκεται είτε στα πρώτα τρία κελιά, είτε στα τελευταία τρία κελιά. Έστω λοιπόν ότι κάναμε μια βολή στο μεσαίο κελί. Χωρίς βλάβη της γενικότητας στο τριγωνικό μισό με την ορθή γωνία κάτω αριστερά. Τότε δεν θα είμαστε σίγουροι ότι βυθίσαμε την βάρκα αφού αυτή μπορεί να βρίσκεται αναποδογυρισμένη στα τελευταία τρία κελιά.
χρειαζόμαστε τουλάχιστον δύο βολές. Πράγματι αν πυροβολήσουμε μόνο μία βολή και η βολή δεν χτυπήσει στο μεσαίο κελί τότε δεν θα είμαστε σίγουροι ότι βυθίσαμε την βάρκα αφού αυτή μπορεί να βρίσκεται είτε στα πρώτα τρία κελιά, είτε στα τελευταία τρία κελιά. Έστω λοιπόν ότι κάναμε μια βολή στο μεσαίο κελί. Χωρίς βλάβη της γενικότητας στο τριγωνικό μισό με την ορθή γωνία κάτω αριστερά. Τότε δεν θα είμαστε σίγουροι ότι βυθίσαμε την βάρκα αφού αυτή μπορεί να βρίσκεται αναποδογυρισμένη στα τελευταία τρία κελιά. βολές. Αυτό επιτυγχάνεται ως εξής. Χωρίζουμε το τετράγωνο σε
βολές. Αυτό επιτυγχάνεται ως εξής. Χωρίζουμε το τετράγωνο σε  τετράγωνα και σε κάθε ένα πυροβολάμε όπως στο σχήμα:
τετράγωνα και σε κάθε ένα πυροβολάμε όπως στο σχήμα: , συμβολίζουμε με
, συμβολίζουμε με 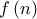 το άθροισμα των πρώτων αριθμών που είναι μικρότεροι του
το άθροισμα των πρώτων αριθμών που είναι μικρότεροι του 
 Ειδικότερα, για κάθε πρώτο αριθμό
Ειδικότερα, για κάθε πρώτο αριθμό  ισχύει
ισχύει  και άρα
και άρα 
 με
με  Τότε, υπάρχει θετικός ακέραιος
Τότε, υπάρχει θετικός ακέραιος  τέτοιος, ώστε
τέτοιος, ώστε  Επίσης, είναι:
Επίσης, είναι:
 και άρα
και άρα 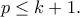


 η ακολουθία των πρώτων. Για
η ακολουθία των πρώτων. Για  ορίζω
ορίζω 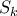 το άθροισμα όλων των πρώτων αριθμών μικρότερων του
το άθροισμα όλων των πρώτων αριθμών μικρότερων του  .
.  ώστε για κάθε
ώστε για κάθε  ο
ο  και άρα
και άρα  για κάποιον θετικό ακέραιο
για κάποιον θετικό ακέραιο 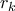 . Τότε
. Τότε 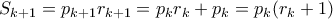
 είναι και
είναι και  και άρα
και άρα  . Δεν μπορούμε όμως να έχουμε
. Δεν μπορούμε όμως να έχουμε  (για
(για  ) αφού τότε είναι
) αφού τότε είναι
 , τότε
, τότε  . Αλλά τότε είναι
. Αλλά τότε είναι  , άτοπο.
, άτοπο.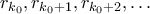 είναι μια αυστηρά φθίνουσα ακολουθία θετικών ακεραίων. Αυτό είναι άτοπο. Άρα το ζητούμενο έπεται. (Υποθέτω ότι
είναι μια αυστηρά φθίνουσα ακολουθία θετικών ακεραίων. Αυτό είναι άτοπο. Άρα το ζητούμενο έπεται. (Υποθέτω ότι 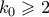 .)
.)