Δίνεται ένα σύνολο θετικών ακεραίων αριθμών
 , όπου
, όπου  είναι περιττός αριθμός με
είναι περιττός αριθμός με  . Μπορούμε να δημιουργήσουμε μια σειρά νέων συνόλων
. Μπορούμε να δημιουργήσουμε μια σειρά νέων συνόλων  με πλήθος στοιχείων τρία το κάθε ένα, έχοντας σε κάθε βήμα τις εξής δύο επιλογές, ξεκινώντας από το
με πλήθος στοιχείων τρία το κάθε ένα, έχοντας σε κάθε βήμα τις εξής δύο επιλογές, ξεκινώντας από το  .
. επιλογή
επιλογήΓια να πάρουμε το
 επιλέγουμε έναν θετικό ακέραιο αριθμό και τον προσθέτουμε σε δύο από τα στοιχεία του
επιλέγουμε έναν θετικό ακέραιο αριθμό και τον προσθέτουμε σε δύο από τα στοιχεία του 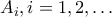 και το τρίτο στοιχείο του
και το τρίτο στοιχείο του  παραμένει το ίδιο και στο σύνολο
παραμένει το ίδιο και στο σύνολο  . (Για παράδειγμα, αν επιλέξω
. (Για παράδειγμα, αν επιλέξω  , τότε το σύνολο
, τότε το σύνολο  μπορεί να είναι
μπορεί να είναι  .)
.) επιλογή
επιλογήΓια να πάρουμε το
 , επιλέγουμε έναν θετικό ακέραιο αριθμό και τον προσθέτουμε σε ένα από τα στοιχεία του
, επιλέγουμε έναν θετικό ακέραιο αριθμό και τον προσθέτουμε σε ένα από τα στοιχεία του 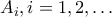 και τον αφαιρούμε από ένα άλλο από τα στοιχεία του
και τον αφαιρούμε από ένα άλλο από τα στοιχεία του  , ενώ το τρίτο στοιχείο του
, ενώ το τρίτο στοιχείο του  παραμένει το ίδιο και στο σύνολο
παραμένει το ίδιο και στο σύνολο  . (Για παράδειγμα, αν επιλέξω
. (Για παράδειγμα, αν επιλέξω  , τότε το σύνολο
, τότε το σύνολο  μπορεί να είναι
μπορεί να είναι  .)
.)Να εξετάσετε αν είναι δυνατόν με αυτή τη διαδικασία σε κάποιο βήμα να έχουμε το σύνολο
 .
.Πρόβλημα 2
Δίνονται τα ψηφία
 . Να βρείτε το άθροισμα όλων των άρτιων τριψήφιων αριθμών που σχηματίζονται από αυτά τα ψηφία αν δεν επιτρέπεται η επανάληψη ψηφίου.
. Να βρείτε το άθροισμα όλων των άρτιων τριψήφιων αριθμών που σχηματίζονται από αυτά τα ψηφία αν δεν επιτρέπεται η επανάληψη ψηφίου.Πρόβλημα 3
Έστω
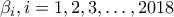 θετικοί ακέραιοι αριθμοί, τέτοιοι ώστε
θετικοί ακέραιοι αριθμοί, τέτοιοι ώστε  .
.Να αποδείξετε ότι:
(α) Για κάθε ακέραιο
 ισχύει:
ισχύει: 
(β) Τουλάχιστον τρεις από τους αριθμούς
 είναι ίσοι.
είναι ίσοι.Πρόβλημα 4
Δίνεται ισόπλευρο τρίγωνο
 . Με κέντρο το
. Με κέντρο το  και ακτίνα
και ακτίνα  γράφουμε κύκλο
γράφουμε κύκλο  . Στο μεγαλύτερο από τα δύο τόξα
. Στο μεγαλύτερο από τα δύο τόξα  του κύκλου
του κύκλου  παίρνουμε σημείο
παίρνουμε σημείο  και φέρουμε τη χορδή
και φέρουμε τη χορδή  . Η παράλληλη από το
. Η παράλληλη από το  προς την
προς την  τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  . Έστω
. Έστω 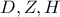 τα μέσα των τμημάτων
τα μέσα των τμημάτων  , αντίστοιχα. Έστω σημείο
, αντίστοιχα. Έστω σημείο  έξω από τον κύκλο και πάνω στην ημιευθεία
έξω από τον κύκλο και πάνω στην ημιευθεία  και ένα σημείο
και ένα σημείο  μέσα στον κύκλο, έτσι ώστε το
μέσα στον κύκλο, έτσι ώστε το  να είναι κυρτό τετράπλευρο με
να είναι κυρτό τετράπλευρο με  και
και  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:(α) το τρίγωνο
 είναι ισόπλευρο
είναι ισόπλευρο(β)



 δεν είναι ίσος με
δεν είναι ίσος με  , οπότε όλοι είναι
, οπότε όλοι είναι 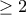 . Έστω κάθε όρος εμφανίζεται το πολύ δύο φορές και έστω
. Έστω κάθε όρος εμφανίζεται το πολύ δύο φορές και έστω  ο μεγαλύτερος παρονομαστής. Τότε το αριστερό μέλος είναι
ο μεγαλύτερος παρονομαστής. Τότε το αριστερό μέλος είναι 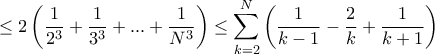
 , άτοπο.
, άτοπο. κι επειδή το
κι επειδή το  είναι μέσο του
είναι μέσο του  η
η  είναι μεσοκάθετη του
είναι μεσοκάθετη του  άρα
άρα 
 είναι
είναι  το
το  είναι εγγράψιμο και
είναι εγγράψιμο και 
 είναι ισόπλευρο.
είναι ισόπλευρο. διέρχεται από τα σημεία
διέρχεται από τα σημεία  και είναι
και είναι  άρα τα σημεία
άρα τα σημεία  είναι
είναι  είναι μεσοκάθετη του
είναι μεσοκάθετη του 
 άρτιος (αφου ν είναι περιττός).
άρτιος (αφου ν είναι περιττός). 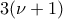 , δηλαδή δεν αλλάζεται.
, δηλαδή δεν αλλάζεται. είναι
είναι  , δηλαδή παραμένει άρτιος.
, δηλαδή παραμένει άρτιος. είναι πάντα άρτιος.
είναι πάντα άρτιος. αριθμούς που τελιώνουν σε 0,
αριθμούς που τελιώνουν σε 0,  αριθμούς που τελιώνουν σε 2 και
αριθμούς που τελιώνουν σε 2 και 
 και
και  , δηλαδή είναι
, δηλαδή είναι 

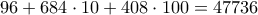
 τέτοιοι αριθμοί, το άθροισμα των ψηφίων των δεκάδων δεν θα μπορούσε να υπερβεί το
τέτοιοι αριθμοί, το άθροισμα των ψηφίων των δεκάδων δεν θα μπορούσε να υπερβεί το  . Αρκετά μικρότερο από το
. Αρκετά μικρότερο από το