Δίνεται η ακολουθία
 με
με  και για
και για  ισχύει
ισχύει .
.Να αποδείξετε ότι:
(α) Ο γενικός όρος της ακολουθίας δίνεται από τον τύπο:

β)
 αν και μόνον αν τουλάχιστον ένας από τους δείκτες
αν και μόνον αν τουλάχιστον ένας από τους δείκτες  είναι άρτιος.
είναι άρτιος.Πρόβλημα 2
Δίνεται ένας φυσικός αριθμός
 . Να αποδείξετε ότι υπάρχει φυσικός αριθμός
. Να αποδείξετε ότι υπάρχει φυσικός αριθμός  , ο οποίος είναι πολλαπλάσιο του
, ο οποίος είναι πολλαπλάσιο του  και έχει ακριβώς
και έχει ακριβώς  θετικούς διαιρέτες.
θετικούς διαιρέτες.Πρόβλημα 3
Δίνονται δύο κύκλοι
 και
και  με
με  , οι οποίοι εφάπτονται εξωτερικά στο σημείο
, οι οποίοι εφάπτονται εξωτερικά στο σημείο  . Από ένα σημείο
. Από ένα σημείο  του κύκλου
του κύκλου  που δεν βρίσκεται πάνω στην ευθεία
που δεν βρίσκεται πάνω στην ευθεία  φέρουμε τις εφαπτόμενες
φέρουμε τις εφαπτόμενες  προς τον κύκλο
προς τον κύκλο  και έστω
και έστω  τα αντίστοιχα σημεία επαφής τους με τον
τα αντίστοιχα σημεία επαφής τους με τον  . Οι ευθείες
. Οι ευθείες  τέμνουν τον κύκλο
τέμνουν τον κύκλο  ξανά στα σημεία
ξανά στα σημεία  , αντίστοιχα. Έστω
, αντίστοιχα. Έστω  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας  και της εφαπτομένης του κύκλου
και της εφαπτομένης του κύκλου  στο σημείο
στο σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
.Πρόβλημα 4
Δίνονται
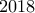 σύνολα. Να αποδείξετε ότι υπάρχουν
σύνολα. Να αποδείξετε ότι υπάρχουν  από αυτά, έστω
από αυτά, έστω  , τέτοια ώστε να ισχύει
, τέτοια ώστε να ισχύει για κάθε
για κάθε  με
με  .
.Δηλαδή η ένωση κάθε δύο από αυτά τα 64 σύνολα είναι ένα σύνολο διαφορετικό από κάθε άλλο από αυτά τα 64 σύνολα.

 την ανάλυσή του σε πρώτους. Τότε ο
την ανάλυσή του σε πρώτους. Τότε ο  κάνει την δουλειά. καθώς
κάνει την δουλειά. καθώς αφού
αφού  και όμοια για τους υπόλοιπους παράγοντες του
και όμοια για τους υπόλοιπους παράγοντες του  ). Επίσης,
). Επίσης,  με χρήση του τύπου ότι το πλήθος των διαιρετών του
με χρήση του τύπου ότι το πλήθος των διαιρετών του  είναι
είναι 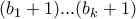 .
. να είναι εφαπτόμενη του
να είναι εφαπτόμενη του  . Επομένως αρκεί το τετράπλευρο
. Επομένως αρκεί το τετράπλευρο  να είναι αρμονικό, καθώς σε αυτή την περίπτωση από γνωστό λήμμα θα ξέρουμε πως οι εφαπτόμενες από το
να είναι αρμονικό, καθώς σε αυτή την περίπτωση από γνωστό λήμμα θα ξέρουμε πως οι εφαπτόμενες από το  και το
και το  θα τέμνονται πάνω στην
θα τέμνονται πάνω στην  .
. τέμνει τον
τέμνει τον 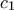 ξανά στο σημείο
ξανά στο σημείο  . Παρατηρούμε πως το τετράπλευρο
. Παρατηρούμε πως το τετράπλευρο  είναι αρμονικό, καθώς οι εφαπτόμενες από το
είναι αρμονικό, καθώς οι εφαπτόμενες από το  και
και  στον
στον  (δηλαδή στο
(δηλαδή στο  (αυτό λέγεται ομοιότητα) με κέντρο το
(αυτό λέγεται ομοιότητα) με κέντρο το  , το
, το  και το
και το  είναι
είναι 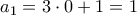 και για
και για  είναι
είναι 
 ισχύει ότι:
ισχύει ότι:
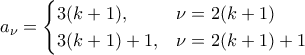
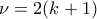 τότε:
τότε: 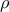 είναι άρτιος, έστω
είναι άρτιος, έστω 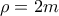 έχουμε:
έχουμε:
 έχουμε:
έχουμε:

 τότε:
τότε: 

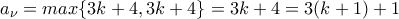
 έχουμε:
έχουμε:
 έχουμε:
έχουμε:
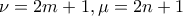 έχουμε:
έχουμε: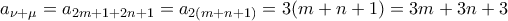


 σύνολα, τότε μπορούμε να βρούμε υποοικογένεια από
σύνολα, τότε μπορούμε να βρούμε υποοικογένεια από  σύνολα με την ιδιότητα η ένωση οποιονδήποτε δύο συνόλων της υποοικογένειας να μην ανήκει στην υποοικογένεια. Το αποτέλεσμα αυτό είναι βέλτιστο.
σύνολα με την ιδιότητα η ένωση οποιονδήποτε δύο συνόλων της υποοικογένειας να μην ανήκει στην υποοικογένεια. Το αποτέλεσμα αυτό είναι βέλτιστο.