Εκπαιδευτικό κέντρο «Σείριος», Σότσι 21-27 Απριλίου 2023
Θέματα της πρώτης μέρας για την 11η τάξη.
1. Ο αριθμός
 είναι τέτοιος, ώστε
είναι τέτοιος, ώστε 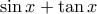 και
και 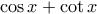 να είναι ρητοί αριθμοί. Να αποδείξετε, ότι ο αριθμός
να είναι ρητοί αριθμοί. Να αποδείξετε, ότι ο αριθμός 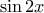 είναι ρίζα δευτεροβάθμιας εξίσωσης με ακέραιους συντελεστές. (Ν. Αγκαχάνοβ)
είναι ρίζα δευτεροβάθμιας εξίσωσης με ακέραιους συντελεστές. (Ν. Αγκαχάνοβ)2.
 μαθητές έχουν μια τράπουλα
μαθητές έχουν μια τράπουλα  καρτών, οι οποίες είναι αριθμημένες με τους αριθμούς από
καρτών, οι οποίες είναι αριθμημένες με τους αριθμούς από  έως
έως  . Ο πρώτος μαθητής ανακατεύει την τράπουλα, ύστερα επιλέγει από την κορυφή της ανακατεμένης τράπουλας μια κάρτα και με κάθε επιλογή κάρτας (συμπεριλαμβανομένης της πρώτης) γράφει στον πίνακα τον αριθμητικό μέσο των αριθμών όλων των καρτών που έχει διαλέξει την δεδομένη στιγμή. Έτσι αυτός γράφει
. Ο πρώτος μαθητής ανακατεύει την τράπουλα, ύστερα επιλέγει από την κορυφή της ανακατεμένης τράπουλας μια κάρτα και με κάθε επιλογή κάρτας (συμπεριλαμβανομένης της πρώτης) γράφει στον πίνακα τον αριθμητικό μέσο των αριθμών όλων των καρτών που έχει διαλέξει την δεδομένη στιγμή. Έτσι αυτός γράφει  αριθμούς και όταν στην τράπουλα απομείνει μια κάρτα, τότε ξανά τοποθετεί της κάρτες στην τράπουλα, στην συνέχεια γίνεται το ίδιο, ξεκινώντας από το ανακάτεμα της τράπουλας, από τον δεύτερο μαθητή. Ύστερα ο τρίτος μαθητής, κ.ο.κ . Να αποδείξετε, ότι μεταξύ των γραμμένων στον πίνακα
αριθμούς και όταν στην τράπουλα απομείνει μια κάρτα, τότε ξανά τοποθετεί της κάρτες στην τράπουλα, στην συνέχεια γίνεται το ίδιο, ξεκινώντας από το ανακάτεμα της τράπουλας, από τον δεύτερο μαθητή. Ύστερα ο τρίτος μαθητής, κ.ο.κ . Να αποδείξετε, ότι μεταξύ των γραμμένων στον πίνακα 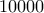 αριθμών θα βρεθούν δυο ίδιοι. (Α. Γκριμπάλκο)
αριθμών θα βρεθούν δυο ίδιοι. (Α. Γκριμπάλκο)3. Σε κάθε γραμμή ενός πίνακα
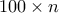 με κάποια σειρά είναι τοποθετημένοι οι αριθμοί από το
με κάποια σειρά είναι τοποθετημένοι οι αριθμοί από το  έως το
έως το  , οι αριθμοί στην γραμμή δεν επαναλαμβάνονται (ο πίνακας έχει
, οι αριθμοί στην γραμμή δεν επαναλαμβάνονται (ο πίνακας έχει  γραμμές και
γραμμές και  στήλες). Επιτρέπεται να ανταλλάξουμε την θέση δυο αριθμών σε μια γραμμή, που διαφέρουν κατά
στήλες). Επιτρέπεται να ανταλλάξουμε την θέση δυο αριθμών σε μια γραμμή, που διαφέρουν κατά  , αν δεν είναι γειτονικοί. Προέκυψε ότι με την βοήθεια τέτοιων πράξεων δεν μπορούμε να λάβουμε δυο ίδιες γραμμές. Για ποιο μέγιστο
, αν δεν είναι γειτονικοί. Προέκυψε ότι με την βοήθεια τέτοιων πράξεων δεν μπορούμε να λάβουμε δυο ίδιες γραμμές. Για ποιο μέγιστο  αυτό είναι δυνατό; (Μ. Αντίποβ)
αυτό είναι δυνατό; (Μ. Αντίποβ)4. Ο κύκλος
 είναι περιγεγραμμένος γύρω από το τρίγωνο
είναι περιγεγραμμένος γύρω από το τρίγωνο  , στο οποίο
, στο οποίο  . Οι διχοτόμοι του τριγώνου
. Οι διχοτόμοι του τριγώνου  τέμνονται στο σημείο
τέμνονται στο σημείο  . Από το μέσο
. Από το μέσο  της πλευράς
της πλευράς  προς την ευθεία
προς την ευθεία  φέρουμε την κάθετο
φέρουμε την κάθετο  . Οι ευθείες
. Οι ευθείες  ,
,  και
και  ορίζουν (οριοθετούν) το τρίγωνο
ορίζουν (οριοθετούν) το τρίγωνο  και οι ευθείες
και οι ευθείες  ,
,  και
και  ορίζουν το τρίγωνο
ορίζουν το τρίγωνο 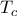 . Οι περιγεγραμμένοι κύκλοι των τριγώνων
. Οι περιγεγραμμένοι κύκλοι των τριγώνων  και
και 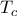 επανατέμνουν τον κύκλο
επανατέμνουν τον κύκλο  στα σημεία
στα σημεία 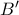 και
και  αντίστοιχα. Να αποδείξετε, ότι το σημείο
αντίστοιχα. Να αποδείξετε, ότι το σημείο  βρίσκεται πάνω στην ευθεία
βρίσκεται πάνω στην ευθεία 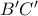 . (Α. Κουζνέτσοβ)
. (Α. Κουζνέτσοβ)
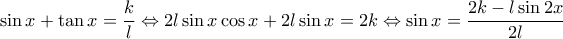
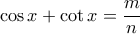 βρίσκω
βρίσκω 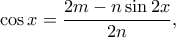 όπου
όπου 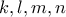 ακέραιοι.
ακέραιοι.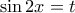 και αντικαταστήσω στην ταυτότητα
και αντικαταστήσω στην ταυτότητα 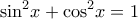 καταλήγω στην εξίσωση
καταλήγω στην εξίσωση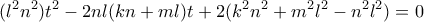 που αποδεικνύει το ζητούμενο.
που αποδεικνύει το ζητούμενο. Έστω
Έστω 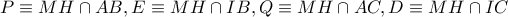 , τότε
, τότε 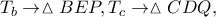 και ας είναι
και ας είναι 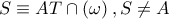 το οποίο προφανώς είναι το μέσο του τόξου του κύκλου
το οποίο προφανώς είναι το μέσο του τόξου του κύκλου 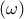 που δεν περιέχει το
που δεν περιέχει το  (αφού
(αφού  του
του  )
)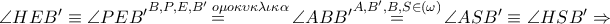
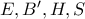 ομοκυκλικά , οπότε
ομοκυκλικά , οπότε 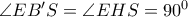 και συνεπώς η
και συνεπώς η 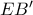 διέρχεται από το αντιδιαμετρικό
διέρχεται από το αντιδιαμετρικό  του
του  ως προς τον
ως προς τον 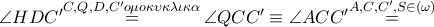
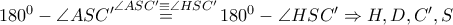 ομοκυκλικά άρα
ομοκυκλικά άρα 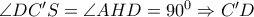 διέρχεται από το
διέρχεται από το 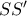 του
του 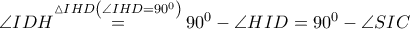
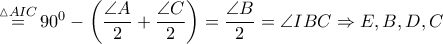 ομοκυκλικά , άρα από το θεώρημα των τεμνομένων χορδών στον εν λόγω περίκυκλο θα έχουμε:
ομοκυκλικά , άρα από το θεώρημα των τεμνομένων χορδών στον εν λόγω περίκυκλο θα έχουμε: 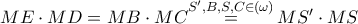 και σύμφωνα με το αντίστροφο του θεωρήματος των τεμνομένων χορδών τα σημεία
και σύμφωνα με το αντίστροφο του θεωρήματος των τεμνομένων χορδών τα σημεία  είναι ομοκυκλικά, άρα
είναι ομοκυκλικά, άρα 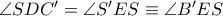 και συνεπώς τα ορθογώνια τρίγωνα
και συνεπώς τα ορθογώνια τρίγωνα 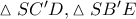 είναι όμοια (ορθογώνια με μια οξεία γωνία ίση) , άρα και
είναι όμοια (ορθογώνια με μια οξεία γωνία ίση) , άρα και 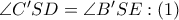
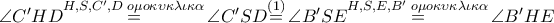 και με
και με 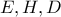 συνευθειακά προκύπτει ότι και
συνευθειακά προκύπτει ότι και 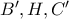 συνευθειακά και το ζητούμενο έχει αποδειχθεί.
συνευθειακά και το ζητούμενο έχει αποδειχθεί.