Ένα Λήμμα
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Ένα Λήμμα
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 2:27 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Λέξεις Κλειδιά:
Re: Ένα Λήμμα
Έστω  η προβολή του
η προβολή του  στην
στην  και
και 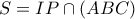 .
.
Θα δείξουμε ότι ομοκυκλικα και ότι
ομοκυκλικα και ότι  συνευθειακα.
συνευθειακα.
Θεωρούμε την αντιστροφή ως προς τον εγγεγραμμένο κύκλο τότε τα πηγαίνουν στα μέσα των
πηγαίνουν στα μέσα των  οπότε ο
οπότε ο  πηγαινει στον κύκλο του Euler του [unparseable or potentially dangerous latex formula] επειδή
πηγαινει στον κύκλο του Euler του [unparseable or potentially dangerous latex formula] επειδή  ανήκει στον
ανήκει στον  θα έχουμε ότι το
θα έχουμε ότι το 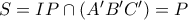 .
.
Επειδή τώρα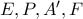 ειναι συνευθειακα τα
ειναι συνευθειακα τα 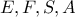 θα είναι ομοκυκλικα αρα και τα
θα είναι ομοκυκλικα αρα και τα  .
.
Το είναι το κέντρο της spiral similarity που στέλνει την
είναι το κέντρο της spiral similarity που στέλνει την  στην
στην  οπότε θα έχουμε:
οπότε θα έχουμε:
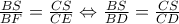
Που δίνει ότι διχοτόμος της
διχοτόμος της 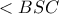 και αρα
και αρα  συνευθειακα.
συνευθειακα.
 η προβολή του
η προβολή του  στην
στην  και
και 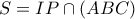 .
.Θα δείξουμε ότι
 ομοκυκλικα και ότι
ομοκυκλικα και ότι  συνευθειακα.
συνευθειακα.Θεωρούμε την αντιστροφή ως προς τον εγγεγραμμένο κύκλο τότε τα
 πηγαίνουν στα μέσα των
πηγαίνουν στα μέσα των  οπότε ο
οπότε ο  πηγαινει στον κύκλο του Euler του [unparseable or potentially dangerous latex formula] επειδή
πηγαινει στον κύκλο του Euler του [unparseable or potentially dangerous latex formula] επειδή  ανήκει στον
ανήκει στον  θα έχουμε ότι το
θα έχουμε ότι το 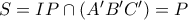 .
.Επειδή τώρα
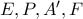 ειναι συνευθειακα τα
ειναι συνευθειακα τα 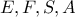 θα είναι ομοκυκλικα αρα και τα
θα είναι ομοκυκλικα αρα και τα  .
.Το
 είναι το κέντρο της spiral similarity που στέλνει την
είναι το κέντρο της spiral similarity που στέλνει την  στην
στην  οπότε θα έχουμε:
οπότε θα έχουμε: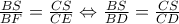
Που δίνει ότι
 διχοτόμος της
διχοτόμος της 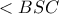 και αρα
και αρα  συνευθειακα.
συνευθειακα.-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Ένα Λήμμα
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 2:28 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Re: Ένα Λήμμα
Κάπως πιο άμεσα. Θα αποδείξουμε πρώτα ότι 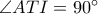 και θα έχουμε το πρώτο ζητούμενο.
και θα έχουμε το πρώτο ζητούμενο.
Όμως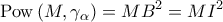 , όπου
, όπου 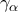 ο κύκλος
ο κύκλος 
Οπότε η ευθεία είναι εφαπτομένη του
είναι εφαπτομένη του 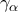 από όπου λαμβάνουμε
από όπου λαμβάνουμε 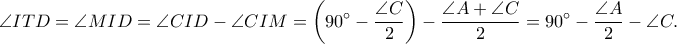
Έπεται ότι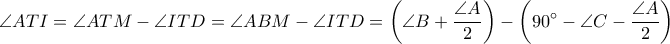
ή ισοδύναμα και το πρώτο ζητούμενο δείχθηκε.
και το πρώτο ζητούμενο δείχθηκε.
Θα αποδείξουμε τώρα και το δεύτερο ζητούμενο. Παρατηρούμε ότι τα σημεία ανήκουν στον κύκλο διαμέτρου
ανήκουν στον κύκλο διαμέτρου  , αφού
, αφού 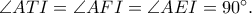 Παίρνουμε
Παίρνουμε  και
και 
Σε συνδυασμό με τις ισότητες γωνιών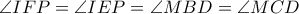 , λαμβάνουμε τελικά ότι
, λαμβάνουμε τελικά ότι  και
και 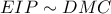 που θα δώσουν
που θα δώσουν 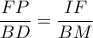 και
και 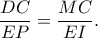
Έχουμε λοιπόν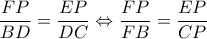 και λόγω του ότι
και λόγω του ότι  , έπεται ότι
, έπεται ότι 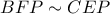 .
.
Από το τελευταίο συμπέρασμα έπονται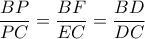 που δίνει ότι η ευθεία
που δίνει ότι η ευθεία  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  , καθώς και
, καθώς και 
Θέτοντας τώρα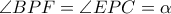 και
και 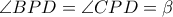 , θα πάρουμε
, θα πάρουμε 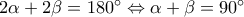 , από όπου και το ζητούμενο.
, από όπου και το ζητούμενο.
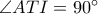 και θα έχουμε το πρώτο ζητούμενο.
και θα έχουμε το πρώτο ζητούμενο. Όμως
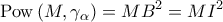 , όπου
, όπου 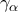 ο κύκλος
ο κύκλος 
Οπότε η ευθεία
 είναι εφαπτομένη του
είναι εφαπτομένη του 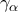 από όπου λαμβάνουμε
από όπου λαμβάνουμε 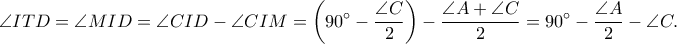
Έπεται ότι
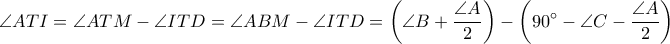
ή ισοδύναμα
 και το πρώτο ζητούμενο δείχθηκε.
και το πρώτο ζητούμενο δείχθηκε.Θα αποδείξουμε τώρα και το δεύτερο ζητούμενο. Παρατηρούμε ότι τα σημεία
 ανήκουν στον κύκλο διαμέτρου
ανήκουν στον κύκλο διαμέτρου  , αφού
, αφού 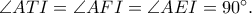 Παίρνουμε
Παίρνουμε  και
και 
Σε συνδυασμό με τις ισότητες γωνιών
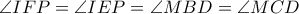 , λαμβάνουμε τελικά ότι
, λαμβάνουμε τελικά ότι  και
και 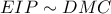 που θα δώσουν
που θα δώσουν 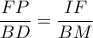 και
και 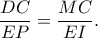
Έχουμε λοιπόν
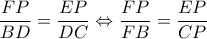 και λόγω του ότι
και λόγω του ότι  , έπεται ότι
, έπεται ότι 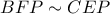 .
.Από το τελευταίο συμπέρασμα έπονται
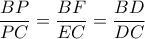 που δίνει ότι η ευθεία
που δίνει ότι η ευθεία  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  , καθώς και
, καθώς και 
Θέτοντας τώρα
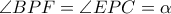 και
και 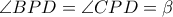 , θα πάρουμε
, θα πάρουμε 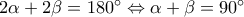 , από όπου και το ζητούμενο.
, από όπου και το ζητούμενο.-
giannimani
- Δημοσιεύσεις: 233
- Εγγραφή: Δευ Μαρ 09, 2009 6:26 pm
- Τοποθεσία: Αθήνα
Re: Ένα Λήμμα
Θεωρούμε τον κύκλο διαμέτρου  που τέμνει τον κύκλο
που τέμνει τον κύκλο  στο σημείο
στο σημείο  .
.
Προφανώς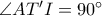 . Αν αποδείξουμε ότι τα σημεία
. Αν αποδείξουμε ότι τα σημεία  ,
,  και
και  ανήκουν στην ίδια ευθεία,
ανήκουν στην ίδια ευθεία,
τότε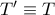 .
.
Τα τρίγωνα και
και 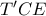 είναι όμοια (
είναι όμοια (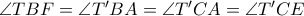 και
και
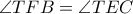 ως παραπληρώματα των ίσων γωνιών
ως παραπληρώματα των ίσων γωνιών 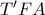 και
και 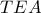 ).
).
Επομένως,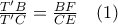
Αλλά, και
και 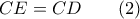
Η λόγω των
λόγω των  γίνεται
γίνεται 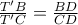 , δηλαδή, η
, δηλαδή, η  διχοτόμος της εγγεγραμμένης γωνίας
διχοτόμος της εγγεγραμμένης γωνίας
στον κύκλο , οπότε η ευθεία
, οπότε η ευθεία  θα περάσει από το μέσο
θα περάσει από το μέσο  του τόξου
του τόξου  ,
,
δηλαδή, το αποδεικτέο. Άμεσα προκύπτει ότι το αντιδιαμετρικό του
αντιδιαμετρικό του  .
.
Έστω τώρα ότι οι παράλληλες ευθείες και
και  (αμφότερες κάθετες στην
(αμφότερες κάθετες στην  ) τέμνουν
) τέμνουν
την ευθεία; στα σημεία
στα σημεία  και
και  αντίστοιχα. Τότε,
αντίστοιχα. Τότε, 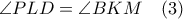 (εντός εναλλάξ).
(εντός εναλλάξ).
Αλλά,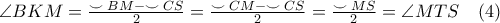
Από τις και
και  έχουμε ότι
έχουμε ότι 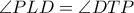 , οπότε το τετράπλευρο
, οπότε το τετράπλευρο 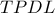 εγγράψιμο.
εγγράψιμο.
Είναι όμως γνωστό ότι η τετράδα είναι αρμονική
είναι αρμονική 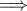 η δέσμη
η δέσμη 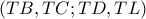
είναι αρμονική, και εφόσον η διχοτόμος της γωνίας
διχοτόμος της γωνίας  , από γνωστό λήμμα
, από γνωστό λήμμα 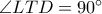 ,
,
οπότε και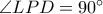 , δηλαδή,
, δηλαδή, 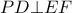 .
.
 που τέμνει τον κύκλο
που τέμνει τον κύκλο  στο σημείο
στο σημείο  .
. Προφανώς
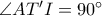 . Αν αποδείξουμε ότι τα σημεία
. Αν αποδείξουμε ότι τα σημεία  ,
,  και
και  ανήκουν στην ίδια ευθεία,
ανήκουν στην ίδια ευθεία,τότε
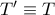 .
.Τα τρίγωνα
 και
και 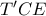 είναι όμοια (
είναι όμοια (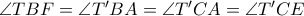 και
και 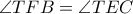 ως παραπληρώματα των ίσων γωνιών
ως παραπληρώματα των ίσων γωνιών 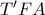 και
και 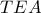 ).
).Επομένως,
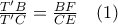
Αλλά,
 και
και 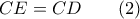
Η
 λόγω των
λόγω των  γίνεται
γίνεται 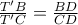 , δηλαδή, η
, δηλαδή, η  διχοτόμος της εγγεγραμμένης γωνίας
διχοτόμος της εγγεγραμμένης γωνίας στον κύκλο
 , οπότε η ευθεία
, οπότε η ευθεία  θα περάσει από το μέσο
θα περάσει από το μέσο  του τόξου
του τόξου  ,
,δηλαδή, το αποδεικτέο. Άμεσα προκύπτει ότι το
 αντιδιαμετρικό του
αντιδιαμετρικό του  .
.Έστω τώρα ότι οι παράλληλες ευθείες
 και
και  (αμφότερες κάθετες στην
(αμφότερες κάθετες στην  ) τέμνουν
) τέμνουν την ευθεία;
 στα σημεία
στα σημεία  και
και  αντίστοιχα. Τότε,
αντίστοιχα. Τότε, 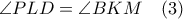 (εντός εναλλάξ).
(εντός εναλλάξ).Αλλά,
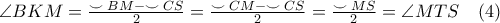
Από τις
 και
και  έχουμε ότι
έχουμε ότι 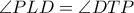 , οπότε το τετράπλευρο
, οπότε το τετράπλευρο 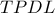 εγγράψιμο.
εγγράψιμο.Είναι όμως γνωστό ότι η τετράδα
 είναι αρμονική
είναι αρμονική 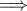 η δέσμη
η δέσμη 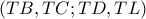
είναι αρμονική, και εφόσον η
 διχοτόμος της γωνίας
διχοτόμος της γωνίας  , από γνωστό λήμμα
, από γνωστό λήμμα 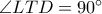 ,
, οπότε και
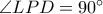 , δηλαδή,
, δηλαδή, 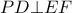 .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες
