1. Να προσδιορίσετε όλα τα διατεταγμένα ζεύγη
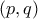 πρώτων αριθμών, που είναι τέτοια, ώστε ο ακέραιος
πρώτων αριθμών, που είναι τέτοια, ώστε ο ακέραιος 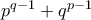 να ισούται με τετράγωνο ακεραίου αριθμού.
να ισούται με τετράγωνο ακεραίου αριθμού. 2. Να προσδιορίσετε όλα τα διατεταγμένα ζεύγη
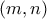 θετικών ακεραίων ,που ικανοποιούν την εξίσωση
θετικών ακεραίων ,που ικανοποιούν την εξίσωση 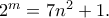
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
Μη αναγνωσμένη δημοσίευση από Dimessi » Κυρ Ιαν 28, 2024 10:38 pm
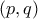 πρώτων αριθμών, που είναι τέτοια, ώστε ο ακέραιος
πρώτων αριθμών, που είναι τέτοια, ώστε ο ακέραιος 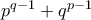 να ισούται με τετράγωνο ακεραίου αριθμού.
να ισούται με τετράγωνο ακεραίου αριθμού. 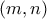 θετικών ακεραίων ,που ικανοποιούν την εξίσωση
θετικών ακεραίων ,που ικανοποιούν την εξίσωση 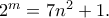
Μη αναγνωσμένη δημοσίευση από Dimessi » Δευ Ιαν 29, 2024 3:34 pm
 περιττοί, τότε οι θετικοί ακέραιοι
περιττοί, τότε οι θετικοί ακέραιοι 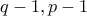 είναι άρτιοι και άρα οι θετικοί ακέραιοι
είναι άρτιοι και άρα οι θετικοί ακέραιοι 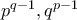 είναι τέλεια τετράγωνα περιττών. Έπεται ότι
είναι τέλεια τετράγωνα περιττών. Έπεται ότι 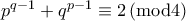 και κατ' επέκταση
και κατ' επέκταση 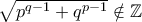 , άτοπο. Άρα, ένας τουλάχιστον από τους
, άτοπο. Άρα, ένας τουλάχιστον από τους  είναι άρτιος. Οπότε έχουμε τις περιπτώσεις:
είναι άρτιος. Οπότε έχουμε τις περιπτώσεις: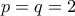 που ικανοποιεί τις συνθήκες, άρα το ζεύγος
που ικανοποιεί τις συνθήκες, άρα το ζεύγος 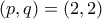 είναι λύση.
είναι λύση. και
και  , άρα παίρνουμε ότι ο θετικός ακέραιος
, άρα παίρνουμε ότι ο θετικός ακέραιος 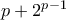 είναι τέλειο τετράγωνο. Θέτουμε
είναι τέλειο τετράγωνο. Θέτουμε 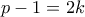 με
με  θετικό ακέραιο για να πάρουμε
θετικό ακέραιο για να πάρουμε 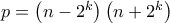 με
με  θετικούς ακεραίους. Επειδή
θετικούς ακεραίους. Επειδή  έπεται
έπεται 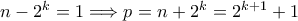 από όπου λαμβάνουμε
από όπου λαμβάνουμε  που είναι άτοπο από την ανισότητα του Bernouli.
που είναι άτοπο από την ανισότητα του Bernouli. 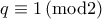 και
και  .
.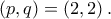
 άρτιος. Γράφουμε
άρτιος. Γράφουμε 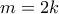 με
με  θετικό ακέραιο για να πάρουμε
θετικό ακέραιο για να πάρουμε 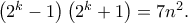 Αφού
Αφού  και ο
και ο  είναι πρώτος, έπεται ότι ένας από τους
είναι πρώτος, έπεται ότι ένας από τους 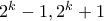 είναι τέλειο τετράγωνο. Για κάθε ακέραιο
είναι τέλειο τετράγωνο. Για κάθε ακέραιο  ισχύει
ισχύει 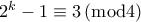 , άρα ο
, άρα ο 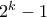 δεν είναι τέλειο τετράγωνο. Δεν γίνεται να είναι
δεν είναι τέλειο τετράγωνο. Δεν γίνεται να είναι  , διότι τότε θα παίρναμε
, διότι τότε θα παίρναμε 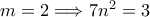 , άτοπο. Επομένως, ο
, άτοπο. Επομένως, ο 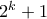 είναι τέλειο τετράγωνο ακεραίου και άμεσα λαμβάνουμε
είναι τέλειο τετράγωνο ακεραίου και άμεσα λαμβάνουμε  Άρα, έχουμε την λύση
Άρα, έχουμε την λύση 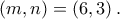
 περιττός. Επειδή
περιττός. Επειδή 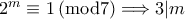 οπότε γράφουμε
οπότε γράφουμε 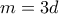 με
με  θετικό ακέραιο. Έπεται ότι
θετικό ακέραιο. Έπεται ότι 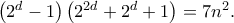 Επειδή ο
Επειδή ο  είναι περιττός έπεται
είναι περιττός έπεται 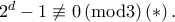 Είναι
Είναι 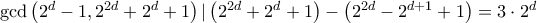 και αφού
και αφού 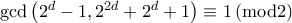 , έπεται ότι
, έπεται ότι 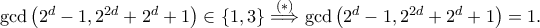 Επομένως έχουμε τις περιπτώσεις:
Επομένως έχουμε τις περιπτώσεις: και
και 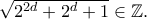 Τότε
Τότε  , άτοπο.
, άτοπο. 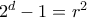 και
και 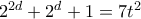 με
με 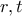 θετικούς ακεραίους. Παίρνουμε
θετικούς ακεραίους. Παίρνουμε 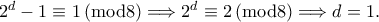 Έπεται ότι
Έπεται ότι 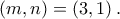
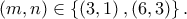
Μη αναγνωσμένη δημοσίευση από stranger » Δευ Ιαν 29, 2024 4:08 pm
Dimessi έγραψε: ↑Δευ Ιαν 29, 2024 3:34 pmΕπειδή είναι απλές, βάζω τις λύσεις μου και για τις δύο .
1. Ανπεριττοί, τότε οι θετικοί ακέραιοι
είναι άρτιοι και άρα οι θετικοί ακέραιοι
είναι τέλεια τετράγωνα περιττών. Έπεται ότι
και κατ' επέκταση
, άτοπο. Άρα, ένας τουλάχιστον από τους
είναι άρτιος. Οπότε έχουμε τις περιπτώσεις:
που ικανοποιεί τις συνθήκες, άρα το ζεύγος
είναι λύση.
και
, άρα παίρνουμε ότι ο θετικός ακέραιος
είναι τέλειο τετράγωνο. Θέτουμε
με
θετικό ακέραιο για να πάρουμε
με
θετικούς ακεραίους. Επειδή
έπεται
από όπου λαμβάνουμε
που είναι άτοπο από την ανισότητα του Bernouli.
Όμοια απορρίπτεται η τρίτη περίπτωση όπουκαι
.
Άρα μοναδική λύση είναι το ζεύγος
2. Περίτπωση1:άρτιος. Γράφουμε
με
θετικό ακέραιο για να πάρουμε
Αφού
και ο
είναι πρώτος, έπεται ότι ένας από τους
είναι τέλειο τετράγωνο. Για κάθε ακέραιο
ισχύει
, άρα ο
δεν είναι τέλειο τετράγωνο. Δεν γίνεται να είναι
, διότι τότε θα παίρναμε
, άτοπο. Επομένως, ο
είναι τέλειο τετράγωνο ακεραίου και άμεσα λαμβάνουμε
Άρα, έχουμε την λύση
Περίπτωση 2:περιττός. Επειδή
οπότε γράφουμε
με
θετικό ακέραιο. Έπεται ότι
Επειδή ο
είναι περιττός έπεται
Είναι
και αφού
, έπεται ότι
Επομένως έχουμε τις περιπτώσεις:
(α)και
Τότε
, άτοπο.
(β)και
με
θετικούς ακεραίους. Παίρνουμε
Έπεται ότι
Οπότε λύσεις είναι τα ζεύγη
Επιστροφή σε “Θέματα διαγωνισμών (ΕΜΕ, ΚΥΜΕ, BMO, JBMO, IMO, Kangaroo κλπ)”
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 6 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off