silouan έγραψε: ↑Τετ Μαρ 13, 2024 7:36 pm
Μπορείς να μας γράψεις την λύση που βασίζεται στην ισότητα με τους λογαρίθμους;
Καλησπέρα Σιλουανέ. Μεταφέρω την λύση χωρίς να την έχω μελετήσει διεξοδικά, οπότε ζητώ την κατανόηση για πιθανά λάθη. Η απόδειξη είναι από το προαναφερθέν βιβλίο με τα προβλήματα της ολυμπιάδας.
Λύση
Θεωρούμε για συντομία


Παρατηρούμε εύκολα, ότι

(13)

και

. (14)

(15)
Μας ζητείται να αποδείξουμε ότι

Μεταφέρουμε τα

στο αριστερό μέλος και με χρήση της ολοκληρωτικής μορφής του λογαρίθμου

έχουμε

(21)
Στην περίπτωση που

, θεωρούμε

. Το ολοκλήρωμα

αναπαριστά το εμβαδόν, που περικλείεται μεταξύ των κατακόρυφων ευθειών
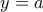
και
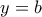
και βρίσκεται μεταξύ της υπερβολής

και του άξονα

. Στο σχήμα τα σκιασμένα με κλίση 135 μοίρες γραμμές εμβαδά τα θεωρούμε με πρόσημο "+" και τα σκιασμένα με 45 μοίρες με πρόσημο "-". Για συντομία το διάστημα
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
στην πρώτη περίπτωση θα το ονομάσουμε θετικό και στην δεύτερη αρνητικό.

- Screenshot 2024-03-13 at 23.28.52.png (86.65 KiB) Προβλήθηκε 300 φορές
Παρατηρούμε, ότι από την συνθήκη (15) προκύπτει ότι, το συνολικό άθροισμα των μηκών των θετικών διαστημάτων είναι ίσο με τα συνολικό μήκος των αρνητικών διαστημάτων. Από την ανισότητα (13) προκύπτει, ότι τα διαστήματα
![[y_{1}, x_{1}], [y_{2}, x_{2}], \ldots , [y_{n-2}, x_{n-2}] [y_{1}, x_{1}], [y_{2}, x_{2}], \ldots , [y_{n-2}, x_{n-2}]](/forum/ext/geomar/texintegr/latexrender/pictures/85775fd1e919aa99205e23f56e17b11f.png)
είναι αρνητικά και δεν τέμνονται. Έτσι, θετικά μπορεί να είναι μόνο τα διαστήματα
![[x_{n-1}, y_{n-1}] [x_{n-1}, y_{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/3b2b645dc99dbb8c418aa477127b2b1c.png)
και
![[x_{n}, y_{n}] [x_{n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/44fde5fc899dd2324a23902e97c0377d.png)
. Δηλαδή, εν γένει ο αριθμός των θετικών διαστημάτων είναι ίσος με

ή

.
1. Εξετάζουμε την περίπτωση όταν υπάρχει ακριβώς ένα θετικό διάστημα. Το αριστερό άκρο του θετικού διαστήματος βρίσκεται αριστερότερα των άλλων διαστημάτων, καθώς

και

για όλα τα

. Εφόσον η συνάρτηση

είναι γνησίως φθίνουσα, τότε η κίνηση του αρνητικού διαστήματος
![[y_{k}, x_{k}] [y_{k}, x_{k}]](/forum/ext/geomar/texintegr/latexrender/pictures/0579c3f888a9f6d76723ba59d7d6db19.png)
αριστερά μόνο αυξάνει το ολοκλήρωμα

, το οποίο το θεωρούμε με πρόσημο "-". Για αυτό με μία τέτοια κίνηση απλά μειώνουμε το αριστερό μέλος της ανισότητας (21). Όταν θα μετακινήσουμε όλα τα αρνητικά διαστήματα δεξιά, τότε αυτά ακριβώς χωρίς επικάλυψει θα χωρέσουν στο θετικό διάστημα
![[x_{n-1}, y_{n-1}] [x_{n-1}, y_{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/3b2b645dc99dbb8c418aa477127b2b1c.png)
, καθώς το μήκος του θετικού διαστήματος είναι ΄σιο με το συνολικό μήκος των αρνητικών διαστημάτων. Συνεπώς, το άθροισμα των ολοκληρωμάτων των μετατοπισμένων διαστημάτων είναι ίσο με μηδέν, που σημαίνει, ότι το άθροισμα των αρχικών ολοκληρωμάτων είναι μη αρνητικό.
2. Αν ο αριθμός των θετικών διαστημάτων είναι ίσος με

, τότε, όπως βρήκαμε, τα αρνητικά διαστήματα δεν τέμνονται. Είναι αρκετό να αποδείξουμε, ότι μετακινώντας τα αρνητικά διαστήματα αριστερά, θα μπορέσουμε να τα χωρέσουμε σε θετικά. Για αυτό όλα τα διαστήματα, που υπάρχουν στο διάστημα
![[x_n}, y_{n}] [x_n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/7c2551b6d090d34e71476df84d03fe46.png)
, θα τα τοποθετήσουμε σε αυτό και τα υπόλοιπα θα τα μετακινήσουμε ακόμα πιο αριστερά στο διάστημα
![[ x_{n-1}, y_{n-1}] [ x_{n-1}, y_{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/090a44c67962183760636b9afc73d4fe.png)
. Εξάλλου, πιθανόν, μπορεί να χρειαστεί ένα από τα αρνητικά διαστήματα να χωριστεί σε δυο κομμάτια. Εφόσον όλα τα αρνητικά διαστήματα βρίσκονται δεξιότερα του

, τότε αρκεί ν ελέγξουμε, ότι το συνολικό μήκος των αρνητικών διαστημάτων που βρίσκονται δεξιότερα του

, δεν είναι μικρότερη από το μήκος του διαστήματος
![[x_{n}, y_{n}] [x_{n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/44fde5fc899dd2324a23902e97c0377d.png)
. Σε αυτήν την περίπτωση με μετατοπίσεις αρνητικών διαστημάτων, που βρίσκονται δεξιότερα του

, αριστερά μπορούμε να επικαλύψουμε το διάστημα
![[x_{n}, y_{n}] [x_{n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/44fde5fc899dd2324a23902e97c0377d.png)
"χωρίς κενά" και τα υπόλοιπα διαστήματα θα χωρέσουν ακριβώς στο διάστημα
![[x_{n-1}, y_{n-1}] [x_{n-1}, y_{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/3b2b645dc99dbb8c418aa477127b2b1c.png)
καθώς ισχύει η ισότητα του αθροίσματος των μηκών των θετικών και αρνητικών διαστημάτων.

- Screenshot 2024-03-13 at 23.29.03.png (34.47 KiB) Προβλήθηκε 300 φορές
Έστω

, σε αυτήν την περίπτωση όλα τα διαστήματα
![[y_{1}, x_{1}] [y_{1}, x_{1}]](/forum/ext/geomar/texintegr/latexrender/pictures/f3bfe6931cf0a298f1ce16f3eb270886.png)
,
![[y_{2}, x_{2}] [y_{2}, x_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/81844e953343f509150f066ffd0bafcd.png)
, ...,
![[y_{k-1}, x_{k-1}] [y_{k-1}, x_{k-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/36b58531f276e3e30754560f486fb7b8.png)
, βρίσκονται δεξιότερα του σημείου

. Επίσης, πιαθνόν, δεξιότερα του σημείου

να βρίσκεται και κομμάτι του διαστήματος
![[y_{k}, x_{k}] [y_{k}, x_{k}]](/forum/ext/geomar/texintegr/latexrender/pictures/0579c3f888a9f6d76723ba59d7d6db19.png)
, το μήκος αυτού του κομματιού είναι ίσο με

(θεωρούμε το μήκος ίσο με μηδέν, αν δεν υπάρχει τέτοιο κομμάτι). Θα δείξουμε, ότι μετακινώντας δεξιά αυτά τα τμήματα, θα μπορέσουμε να επικαλύψουμε το διάστημα
![[x_{n}, y_{n}] [x_{n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/44fde5fc899dd2324a23902e97c0377d.png)
. Για αυτό είναι αρκετό να ελέγξουμε, ότι

μετά την εφαρμογή του λήμματος 1 και το άνοιγμα των παρενθέσεων καταλήγουμε στην ανισότητα

,
η οποία προκύπτει από το άθροισμα των ανισοτήτων

,

,

Με αυτό το τρόπο, ακόμα και όταν υπάρχουν δυο θετικά διαστήματα, μετακινώντας δεξιά αρνητικά διαστήματα, μπορούμε να τα χωρέσουμε χωρίς επικάλυψη στα θετικά διαστήματα. Το άθροισμα των ολοκήρωμάτων των μετατοπισμένων διαστημάτων είναι ίσο με μηδέν και άρα το άθροισμα των αρχικών ολοκληρωμάτων είναι μη αρνητικό. Η Μογγολική ανισότητα αποδείχθηκε.
 Λήμμα 1.
Λήμμα 1.
Για


.
Απόδειξη. Παρτηρούμε ότι

, από όπου

.

 , και ο Γιώργος μετακινεί το πιόνι σε απόσταση, που ανακοίνωσε ο Νίκος, σε οποιαδήποτε κατεύθυνση. Εξάλλου απαγορεύεται δέκα συνεχόμενες φορές να μετακινηθεί το πιόνι προς την ίδια κατεύθυνση. Μπορεί άραγε ο Νίκος να ανακοινώσει τέτοιους αριθμούς, ώστε μετά από κάποια χρονική στιγμή το πιόνι να βρεθεί σε απόσταση μεγαλύτερη του
, και ο Γιώργος μετακινεί το πιόνι σε απόσταση, που ανακοίνωσε ο Νίκος, σε οποιαδήποτε κατεύθυνση. Εξάλλου απαγορεύεται δέκα συνεχόμενες φορές να μετακινηθεί το πιόνι προς την ίδια κατεύθυνση. Μπορεί άραγε ο Νίκος να ανακοινώσει τέτοιους αριθμούς, ώστε μετά από κάποια χρονική στιγμή το πιόνι να βρεθεί σε απόσταση μεγαλύτερη του  από την αρχική του θέση; (Σ. Μπέρλοβ)
από την αρχική του θέση; (Σ. Μπέρλοβ) και του άλλου στα σημεία
και του άλλου στα σημεία  . Να αποδείξετε, ότι τα τρίγωνα
. Να αποδείξετε, ότι τα τρίγωνα  και
και  έχουν κοινό ορθόκεντρο. (Τ. Εμελιάνοβα, Λ. Εμελιάνοβ)
έχουν κοινό ορθόκεντρο. (Τ. Εμελιάνοβα, Λ. Εμελιάνοβ) έχει την ακόλουθη ιδιότητα: για οποιουσδήποτε φυσικούς αριθμούς
έχει την ακόλουθη ιδιότητα: για οποιουσδήποτε φυσικούς αριθμούς  και
και  (μη μηδενικούς) ο αριθμός
(μη μηδενικούς) ο αριθμός  , είναι ακέραιος. Να αποδείξετε ότι αυτό το πολυώνυμο διαιρείτε με το
, είναι ακέραιος. Να αποδείξετε ότι αυτό το πολυώνυμο διαιρείτε με το  . (Φ. Πετρόβ)
. (Φ. Πετρόβ) του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  δίνεται ένα σημείο
δίνεται ένα σημείο  . Οι ευθείες
. Οι ευθείες  και
και  τέμνουν την προέκταση των πλευρών
τέμνουν την προέκταση των πλευρών  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα και η ευθεία
αντίστοιχα και η ευθεία  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Οι ευθείες
. Οι ευθείες  και
και  τέμνουν τις πλευρές
τέμνουν τις πλευρές  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα. Να αποδείξετε ότι η ευθεία
αντίστοιχα. Να αποδείξετε ότι η ευθεία  διέρχεται από το σημείο τομής των συμμετροδιάμεσων του τριγώνου
διέρχεται από το σημείο τομής των συμμετροδιάμεσων του τριγώνου  . (Λ. Εμελιάνοβ)
. (Λ. Εμελιάνοβ) γράφος χωρίς τρίγωνα, στον οποίο μπορούμε να διαλέξουμε το πολύ
γράφος χωρίς τρίγωνα, στον οποίο μπορούμε να διαλέξουμε το πολύ  ζεύγη μη γειτονικών ακμών. Να αποδείξετε ότι οι κορυφές του επιδέχονται κανονικό χρωματισμό με
ζεύγη μη γειτονικών ακμών. Να αποδείξετε ότι οι κορυφές του επιδέχονται κανονικό χρωματισμό με  χρώματα. (Β. Ντόλνικοβ, Σ. Μπέρλοβ)
χρώματα. (Β. Ντόλνικοβ, Σ. Μπέρλοβ) οι αριθμοί
οι αριθμοί  (
( ) δίνουν ανά δυο διαφορετικά υπόλοιπα στην διαίρεση με το
) δίνουν ανά δυο διαφορετικά υπόλοιπα στην διαίρεση με το  . (Ντ. Τζούκιτς)
. (Ντ. Τζούκιτς) ισχύει η ανισότητα:
ισχύει η ανισότητα:
 . (Α. Χράμπροβ)
. (Α. Χράμπροβ) σφαιρών στον χώρο με ακτίνες
σφαιρών στον χώρο με ακτίνες  μπορεί να επικαλυφτεί με σφαίρα ακτίνας
μπορεί να επικαλυφτεί με σφαίρα ακτίνας  . (Φ. Πετρόβ)
. (Φ. Πετρόβ)
 που δεν έχουν κοινή πλευρά ούτε κοινή κορυφή, είναι τοποθετημένα ώστε να αντιστοιχούν οι πλευρές τους κατά σειρά, αλλά και οι κορυφές τους και οι ευθείες
που δεν έχουν κοινή πλευρά ούτε κοινή κορυφή, είναι τοποθετημένα ώστε να αντιστοιχούν οι πλευρές τους κατά σειρά, αλλά και οι κορυφές τους και οι ευθείες  να συντρέχουν, τότε, οι ευθείες που ανήκουν οι αντίστοιχες πλευρές των τριγώνων τέμνονται σε σημεία που βρίσκονται σε ευθεία, και αντιστρόφως».
να συντρέχουν, τότε, οι ευθείες που ανήκουν οι αντίστοιχες πλευρές των τριγώνων τέμνονται σε σημεία που βρίσκονται σε ευθεία, και αντιστρόφως».  τα σημεία
τα σημεία  ανήκουν στην ίδια
ανήκουν στην ίδια  συντρέχουν με τις ευθείες
συντρέχουν με τις ευθείες  να είναι οι δύο
να είναι οι δύο 
 , που ικανοποιούν την συνθήκη
, που ικανοποιούν την συνθήκη  , ισχύει ανισότητα
, ισχύει ανισότητα
 , η τελευταία και χωρίς την συνθήκη της διάταξης (π.χ. όπως δόθηκε στην ολυμπιάδα της Α. Πετρούπολης). Για αρκετό καιρό απόδειξη για την ανισότητα στην γενική της μορφή δεν είχε εμφανιστεί. Μάλιστα είχε προκύψει η εικασία ότι όπως και στην ανισότητα
, η τελευταία και χωρίς την συνθήκη της διάταξης (π.χ. όπως δόθηκε στην ολυμπιάδα της Α. Πετρούπολης). Για αρκετό καιρό απόδειξη για την ανισότητα στην γενική της μορφή δεν είχε εμφανιστεί. Μάλιστα είχε προκύψει η εικασία ότι όπως και στην ανισότητα  , η οποία παρουσιάζεται στην παράγραφο 6 (του εν λόγου άρθρου), πρότεινε το 1999 ο Ντ. Σ. Τσελκάκ. Μετά από ένα χρόνο περίπου ο Σ.Ε. Ρούκσιν ενημέρωσε τον αρθρογράφο (Χραμπρόβ) ότι η ανισότητα μπορεί να εξαχθεί από την ανισότητα Karamata. Αργότερα έγινε γνωστό ότι απόδειξη της Μογγολικής ανισότητας είχε δημοσιοποιηθεί ήδη το 1998 στο βιβλίο των Ν.Μ. Σεντριακιάν και Α.Μ. Αβοιάν "Ανισότητες, Μέθοδοι αποδείξεων, Γερεβάν 1998". Το βιβλίο αυτό λόγω του ότι ήταν γραμμένο στα αρμένικα δεν ήταν ευρέως διαδεδομένο, μέχρι να εμφανιστεί ρωσική μετάφραση.
, η οποία παρουσιάζεται στην παράγραφο 6 (του εν λόγου άρθρου), πρότεινε το 1999 ο Ντ. Σ. Τσελκάκ. Μετά από ένα χρόνο περίπου ο Σ.Ε. Ρούκσιν ενημέρωσε τον αρθρογράφο (Χραμπρόβ) ότι η ανισότητα μπορεί να εξαχθεί από την ανισότητα Karamata. Αργότερα έγινε γνωστό ότι απόδειξη της Μογγολικής ανισότητας είχε δημοσιοποιηθεί ήδη το 1998 στο βιβλίο των Ν.Μ. Σεντριακιάν και Α.Μ. Αβοιάν "Ανισότητες, Μέθοδοι αποδείξεων, Γερεβάν 1998". Το βιβλίο αυτό λόγω του ότι ήταν γραμμένο στα αρμένικα δεν ήταν ευρέως διαδεδομένο, μέχρι να εμφανιστεί ρωσική μετάφραση. η ανισότητα ισχύει μόνο για
η ανισότητα ισχύει μόνο για  . Για
. Για  ανάγεται στην ανισότητα αριθμητικού - γεωμετρικού μέσου.
ανάγεται στην ανισότητα αριθμητικού - γεωμετρικού μέσου.

 (13)
(13) και
και  . (14)
. (14) (15)
(15)
 στο αριστερό μέλος και με χρήση της ολοκληρωτικής μορφής του λογαρίθμου
στο αριστερό μέλος και με χρήση της ολοκληρωτικής μορφής του λογαρίθμου  (21)
(21) , θεωρούμε
, θεωρούμε  . Το ολοκλήρωμα
. Το ολοκλήρωμα  αναπαριστά το εμβαδόν, που περικλείεται μεταξύ των κατακόρυφων ευθειών
αναπαριστά το εμβαδόν, που περικλείεται μεταξύ των κατακόρυφων ευθειών 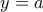 και
και 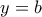 και βρίσκεται μεταξύ της υπερβολής
και βρίσκεται μεταξύ της υπερβολής  και του άξονα
και του άξονα  . Στο σχήμα τα σκιασμένα με κλίση 135 μοίρες γραμμές εμβαδά τα θεωρούμε με πρόσημο "+" και τα σκιασμένα με 45 μοίρες με πρόσημο "-". Για συντομία το διάστημα
. Στο σχήμα τα σκιασμένα με κλίση 135 μοίρες γραμμές εμβαδά τα θεωρούμε με πρόσημο "+" και τα σκιασμένα με 45 μοίρες με πρόσημο "-". Για συντομία το διάστημα ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) στην πρώτη περίπτωση θα το ονομάσουμε θετικό και στην δεύτερη αρνητικό.
στην πρώτη περίπτωση θα το ονομάσουμε θετικό και στην δεύτερη αρνητικό. ![[y_{1}, x_{1}], [y_{2}, x_{2}], \ldots , [y_{n-2}, x_{n-2}] [y_{1}, x_{1}], [y_{2}, x_{2}], \ldots , [y_{n-2}, x_{n-2}]](/forum/ext/geomar/texintegr/latexrender/pictures/85775fd1e919aa99205e23f56e17b11f.png)
![[x_{n-1}, y_{n-1}] [x_{n-1}, y_{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/3b2b645dc99dbb8c418aa477127b2b1c.png) και
και ![[x_{n}, y_{n}] [x_{n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/44fde5fc899dd2324a23902e97c0377d.png) . Δηλαδή, εν γένει ο αριθμός των θετικών διαστημάτων είναι ίσος με
. Δηλαδή, εν γένει ο αριθμός των θετικών διαστημάτων είναι ίσος με  .
. και
και  για όλα τα
για όλα τα  . Εφόσον η συνάρτηση
. Εφόσον η συνάρτηση  είναι γνησίως φθίνουσα, τότε η κίνηση του αρνητικού διαστήματος
είναι γνησίως φθίνουσα, τότε η κίνηση του αρνητικού διαστήματος ![[y_{k}, x_{k}] [y_{k}, x_{k}]](/forum/ext/geomar/texintegr/latexrender/pictures/0579c3f888a9f6d76723ba59d7d6db19.png) αριστερά μόνο αυξάνει το ολοκλήρωμα
αριστερά μόνο αυξάνει το ολοκλήρωμα  , το οποίο το θεωρούμε με πρόσημο "-". Για αυτό με μία τέτοια κίνηση απλά μειώνουμε το αριστερό μέλος της ανισότητας (21). Όταν θα μετακινήσουμε όλα τα αρνητικά διαστήματα δεξιά, τότε αυτά ακριβώς χωρίς επικάλυψει θα χωρέσουν στο θετικό διάστημα
, το οποίο το θεωρούμε με πρόσημο "-". Για αυτό με μία τέτοια κίνηση απλά μειώνουμε το αριστερό μέλος της ανισότητας (21). Όταν θα μετακινήσουμε όλα τα αρνητικά διαστήματα δεξιά, τότε αυτά ακριβώς χωρίς επικάλυψει θα χωρέσουν στο θετικό διάστημα ![[x_n}, y_{n}] [x_n}, y_{n}]](/forum/ext/geomar/texintegr/latexrender/pictures/7c2551b6d090d34e71476df84d03fe46.png) , θα τα τοποθετήσουμε σε αυτό και τα υπόλοιπα θα τα μετακινήσουμε ακόμα πιο αριστερά στο διάστημα
, θα τα τοποθετήσουμε σε αυτό και τα υπόλοιπα θα τα μετακινήσουμε ακόμα πιο αριστερά στο διάστημα ![[ x_{n-1}, y_{n-1}] [ x_{n-1}, y_{n-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/090a44c67962183760636b9afc73d4fe.png) . Εξάλλου, πιθανόν, μπορεί να χρειαστεί ένα από τα αρνητικά διαστήματα να χωριστεί σε δυο κομμάτια. Εφόσον όλα τα αρνητικά διαστήματα βρίσκονται δεξιότερα του
. Εξάλλου, πιθανόν, μπορεί να χρειαστεί ένα από τα αρνητικά διαστήματα να χωριστεί σε δυο κομμάτια. Εφόσον όλα τα αρνητικά διαστήματα βρίσκονται δεξιότερα του  , τότε αρκεί ν ελέγξουμε, ότι το συνολικό μήκος των αρνητικών διαστημάτων που βρίσκονται δεξιότερα του
, τότε αρκεί ν ελέγξουμε, ότι το συνολικό μήκος των αρνητικών διαστημάτων που βρίσκονται δεξιότερα του  , δεν είναι μικρότερη από το μήκος του διαστήματος
, δεν είναι μικρότερη από το μήκος του διαστήματος  , σε αυτήν την περίπτωση όλα τα διαστήματα
, σε αυτήν την περίπτωση όλα τα διαστήματα ![[y_{1}, x_{1}] [y_{1}, x_{1}]](/forum/ext/geomar/texintegr/latexrender/pictures/f3bfe6931cf0a298f1ce16f3eb270886.png) ,
, ![[y_{2}, x_{2}] [y_{2}, x_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/81844e953343f509150f066ffd0bafcd.png) , ...,
, ..., ![[y_{k-1}, x_{k-1}] [y_{k-1}, x_{k-1}]](/forum/ext/geomar/texintegr/latexrender/pictures/36b58531f276e3e30754560f486fb7b8.png) , βρίσκονται δεξιότερα του σημείου
, βρίσκονται δεξιότερα του σημείου  (θεωρούμε το μήκος ίσο με μηδέν, αν δεν υπάρχει τέτοιο κομμάτι). Θα δείξουμε, ότι μετακινώντας δεξιά αυτά τα τμήματα, θα μπορέσουμε να επικαλύψουμε το διάστημα
(θεωρούμε το μήκος ίσο με μηδέν, αν δεν υπάρχει τέτοιο κομμάτι). Θα δείξουμε, ότι μετακινώντας δεξιά αυτά τα τμήματα, θα μπορέσουμε να επικαλύψουμε το διάστημα 
 ,
, ,
, ,
,


 .
. , από όπου
, από όπου .
.