 . Να βρεθεί ο αριθμός των διακεκριμένων πραγματικών λύσεων της
. Να βρεθεί ο αριθμός των διακεκριμένων πραγματικών λύσεων της 
Συντονιστής: Demetres
 και
και  για κάθε θετικό ακέραιο
για κάθε θετικό ακέραιο  .
. και
και  για κάθε
για κάθε  με
με  και κάθε
και κάθε  .
. και κάθε
και κάθε  , η εξίσωση
, η εξίσωση 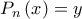 έχει ακριβώς δύο πραγματικές ρίζες.
έχει ακριβώς δύο πραγματικές ρίζες. , έχουμε:
, έχουμε: .
. . Τότε, έχουμε ότι:
. Τότε, έχουμε ότι: ,
, για κάθε
για κάθε  . Άρα, ο Ισχυρισμός έπεται επαγωγικά.
. Άρα, ο Ισχυρισμός έπεται επαγωγικά. 
 , η εξίσωση
, η εξίσωση  έχει ακριβώς
έχει ακριβώς  πραγματικές ρίζες.
πραγματικές ρίζες. και
και  έχουμε:
έχουμε: ,
, .
. . Τότε, έχουμε ότι:
. Τότε, έχουμε ότι: .
.
 ,
, πραγματικές ρίζες, από την επαγωγική υπόθεση.
πραγματικές ρίζες, από την επαγωγική υπόθεση. 
 ,
, έχει ακριβώς
έχει ακριβώς  πραγματικές ρίζες, οπότε το συμπέρασμα έπεται επαγωγικά.
πραγματικές ρίζες, οπότε το συμπέρασμα έπεται επαγωγικά. 
 έχει ακριβώς
έχει ακριβώς  πραγματικές ρίζες.
πραγματικές ρίζες.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες