 για τους οποίους υπάρχει πραγματικό πολυώνυμο
για τους οποίους υπάρχει πραγματικό πολυώνυμο  ώστε να ισχύουν τα ακόλουθα:
ώστε να ισχύουν τα ακόλουθα:(α) Όλοι οι συντελεστές του
 είναι μη αρνητικοί, και
είναι μη αρνητικοί, και(β) το
 είναι ρίζα του
είναι ρίζα του  .
. [Επεξεργασία: Βελτίωση εκφώνησης.]
Συντονιστής: Demetres
 για τους οποίους υπάρχει πραγματικό πολυώνυμο
για τους οποίους υπάρχει πραγματικό πολυώνυμο  ώστε να ισχύουν τα ακόλουθα:
ώστε να ισχύουν τα ακόλουθα: είναι μη αρνητικοί, και
είναι μη αρνητικοί, και είναι ρίζα του
είναι ρίζα του  .
.  θετικός πραγματικός, τότε προφανώς δεν υπάρχει τέτοιο πολυώνυμο. Θα δείξουμε ότι σε όλες τις άλλες περιπτώσεις υπάρχει.
θετικός πραγματικός, τότε προφανώς δεν υπάρχει τέτοιο πολυώνυμο. Θα δείξουμε ότι σε όλες τις άλλες περιπτώσεις υπάρχει.  παίρνουμε
παίρνουμε  . Οπότε μπορούμε να υποθέσουμε ότι
. Οπότε μπορούμε να υποθέσουμε ότι  με
με 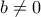 . Για θετικό ακέραιο
. Για θετικό ακέραιο  , ορίζουμε πραγματικά πολυώνυμα
, ορίζουμε πραγματικά πολυώνυμα και
και 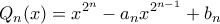
 ορίζονται με τις πιο κάτω αναδρομικές σχέσεις:
ορίζονται με τις πιο κάτω αναδρομικές σχέσεις: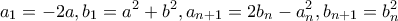
 είναι ρίζα του
είναι ρίζα του 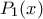 . Επαγωγικά είναι ρίζα του
. Επαγωγικά είναι ρίζα του  για κάθε
για κάθε  , αφού
, αφού  .
. ώστε
ώστε  . Ορίζω
. Ορίζω  Αρκεί να δείξω ότι
Αρκεί να δείξω ότι  για κάποιον
για κάποιον  αφού τότε θα είναι
αφού τότε θα είναι  .
. ικανοποιεί τον αναδρομικό τύπο
ικανοποιεί τον αναδρομικό τύπο
 για κάθε
για κάθε  . Έχουμε επίσης την αρχική συνθήκη
. Έχουμε επίσης την αρχική συνθήκη  Τότε όμως είναι
Τότε όμως είναι![\displaystyle{ c_{n+1} - c_n = \frac{c_n}{(1-2c_n)^2}\left[ c_n - (1-2c_n)^2\right] = \frac{c_n(5c_n - 1 - 4c_n^2)}{(1-2c_n)^2} = \frac{c_n(4c_n - 1)(1-c_n)}{(1-2c_n)^2}} \displaystyle{ c_{n+1} - c_n = \frac{c_n}{(1-2c_n)^2}\left[ c_n - (1-2c_n)^2\right] = \frac{c_n(5c_n - 1 - 4c_n^2)}{(1-2c_n)^2} = \frac{c_n(4c_n - 1)(1-c_n)}{(1-2c_n)^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/f0006bc0ba796861aad919a192644476.png)
 είναι αύξουσα και άνω φραγμένη από το
είναι αύξουσα και άνω φραγμένη από το  . Άρα τείνει σε κάποιο όριο
. Άρα τείνει σε κάποιο όριο  . Παίρνοντας όρια στην αναδρομική σχέση λαμβάνουμε
. Παίρνοντας όρια στην αναδρομική σχέση λαμβάνουμε
 , οπότε
, οπότε  ή
ή  . Και τα δύο όμως απορρίπτονται. Οπότε όντως
. Και τα δύο όμως απορρίπτονται. Οπότε όντως  για κάποιο
για κάποιο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες