 και
και  μήκους
μήκους  . Δείξτε ότι υπάρχουν φυσικοί αριθμοί
. Δείξτε ότι υπάρχουν φυσικοί αριθμοί  και
και  τέτοιοι ώστε οι ακολουθίες να διαφέρουν στο πλήθος των άσσων που υπάρχουν στις θέσεις που οι αριθμοί τους είναι ισοϋπόλοιποι με
τέτοιοι ώστε οι ακολουθίες να διαφέρουν στο πλήθος των άσσων που υπάρχουν στις θέσεις που οι αριθμοί τους είναι ισοϋπόλοιποι με  .
.Συντονιστής: Demetres
 και
και  μήκους
μήκους  . Δείξτε ότι υπάρχουν φυσικοί αριθμοί
. Δείξτε ότι υπάρχουν φυσικοί αριθμοί  και
και  τέτοιοι ώστε οι ακολουθίες να διαφέρουν στο πλήθος των άσσων που υπάρχουν στις θέσεις που οι αριθμοί τους είναι ισοϋπόλοιποι με
τέτοιοι ώστε οι ακολουθίες να διαφέρουν στο πλήθος των άσσων που υπάρχουν στις θέσεις που οι αριθμοί τους είναι ισοϋπόλοιποι με  .
. είναι
είναι  και το ζητούμενο είναι προφανές παίρνοντας
και το ζητούμενο είναι προφανές παίρνοντας  και
και  οποιαδήποτε θέση στην οποία διαφέρουν οι ακολουθίες. Μπορούμε λοιπόν να υποθέσουμε ότι
οποιαδήποτε θέση στην οποία διαφέρουν οι ακολουθίες. Μπορούμε λοιπόν να υποθέσουμε ότι  .
. το σύνολο των θέσεων όπου η πρώτη ακολουθία έχει άσσους, και
το σύνολο των θέσεων όπου η πρώτη ακολουθία έχει άσσους, και  το σύνολο των θέσεων όπου η δεύτερη ακολουθία έχει άσσους. Ορίζουμε
το σύνολο των θέσεων όπου η δεύτερη ακολουθία έχει άσσους. Ορίζουμε
 είναι μη μηδενικό πολυώνυμο βαθμού το πολύ
είναι μη μηδενικό πολυώνυμο βαθμού το πολύ  . Επίσης, για κάθε
. Επίσης, για κάθε  , αν θέσουμε
, αν θέσουμε  έχουμε
έχουμε  για κάθε
για κάθε  αφού κάθε
αφού κάθε  με
με 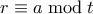 συνεισφέρει
συνεισφέρει  στο
στο  , και κάθε
, και κάθε  με
με  συνεισφέρει
συνεισφέρει  στο
στο  .
. 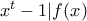 για κάθε
για κάθε  .
.  , και
, και  . Για
. Για  έχουμε
έχουμε 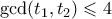 οπότε
οπότε 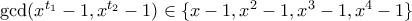 .
. , όλα τα πολυώνυμα
, όλα τα πολυώνυμα 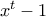 είναι πολλαπλάσια του
είναι πολλαπλάσια του  .
. ακέραιοι
ακέραιοι  , ώστε το πολυώνυμο
, ώστε το πολυώνυμο 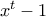 να είναι πολλαπλάσιο του
να είναι πολλαπλάσιο του 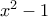 .
. ακέραιοι
ακέραιοι  , ώστε το πολυώνυμο
, ώστε το πολυώνυμο 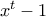 να είναι πολλαπλάσιο του
να είναι πολλαπλάσιο του  .
. ακέραιοι
ακέραιοι  , ώστε το πολυώνυμο
, ώστε το πολυώνυμο 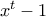 να είναι πολλαπλάσιο του
να είναι πολλαπλάσιο του 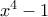 .
. διαιρεί το πολυώνυμο
διαιρεί το πολυώνυμο 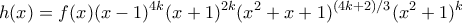
 είναι το πολύ
είναι το πολύ 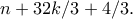
 είναι τουλάχιστον
είναι τουλάχιστον
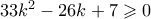 που ισχύει αφού
που ισχύει αφού  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες