Να υπολογίσετε το
![\lim_{n\rightarrow \infty }\sum_{k=0}^{[n/2]}\binom{n}{2k}(-1)^k\frac{1}{n^{2k}} \lim_{n\rightarrow \infty }\sum_{k=0}^{[n/2]}\binom{n}{2k}(-1)^k\frac{1}{n^{2k}}](/forum/ext/geomar/texintegr/latexrender/pictures/d94f37a50a9ce953071634c3074d673f.png) .
.Συντονιστής: Demetres
![\lim_{n\rightarrow \infty }\sum_{k=0}^{[n/2]}\binom{n}{2k}(-1)^k\frac{1}{n^{2k}} \lim_{n\rightarrow \infty }\sum_{k=0}^{[n/2]}\binom{n}{2k}(-1)^k\frac{1}{n^{2k}}](/forum/ext/geomar/texintegr/latexrender/pictures/d94f37a50a9ce953071634c3074d673f.png) .
.Θα δώσω μια απόδειξη χωρίς μιγαδικούς.Λάμπρος Κατσάπας έγραψε: ↑Κυρ Φεβ 25, 2018 3:11 pmΚατά την επίλυση ενός προβλήματος μου προέκυψε το παρακάτω όριο. Δεν δίνω την τιμή του γιατί μάλλον θα ''καρφώσω'' την μέθοδο. Για όποιον θέλει να ασχοληθεί λοιπόν:
Να υπολογίσετε το.
![a_{n}=\sum_{k=0}^{[n/2]}\binom{n}{2k}(-1)^k\frac{1}{n^{2k}} a_{n}=\sum_{k=0}^{[n/2]}\binom{n}{2k}(-1)^k\frac{1}{n^{2k}}](/forum/ext/geomar/texintegr/latexrender/pictures/4aa7da4cff80406aeff62390914003b6.png)
![b_{n}=\sum_{k=0}^{[n/2]}(-1)^k\frac{1}{(2k)!} b_{n}=\sum_{k=0}^{[n/2]}(-1)^k\frac{1}{(2k)!}](/forum/ext/geomar/texintegr/latexrender/pictures/d92cc8807e7c7a0d8f2a9469425d3a2a.png)
![b_{n}-a_{n}=\sum_{k=0}^{[n/2]}(-1)^k\frac{1}{(2k)!}(1-\dfrac{n(n-1)..(n-2k+1)}{n^{2k}}) b_{n}-a_{n}=\sum_{k=0}^{[n/2]}(-1)^k\frac{1}{(2k)!}(1-\dfrac{n(n-1)..(n-2k+1)}{n^{2k}})](/forum/ext/geomar/texintegr/latexrender/pictures/bad545e80dc68deefd0a8cfb27ffe5dc.png) (1)
(1)
![\left | b_{n}-a_{n} \right |\leq \sum_{k=1}^{[\frac{n}{2}]}\frac{1}{(2k)!}\frac{(2k-1)2k}{2n}=\sum_{k=1}^{[\frac{n}{2}]}\frac{1}{(2(k-1)!}\frac{1}{2n}\leq \frac{c_{1}}{n} \left | b_{n}-a_{n} \right |\leq \sum_{k=1}^{[\frac{n}{2}]}\frac{1}{(2k)!}\frac{(2k-1)2k}{2n}=\sum_{k=1}^{[\frac{n}{2}]}\frac{1}{(2(k-1)!}\frac{1}{2n}\leq \frac{c_{1}}{n}](/forum/ext/geomar/texintegr/latexrender/pictures/5497db3274d5b5be5a95daf14dbd23a5.png)
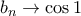

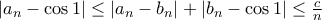
 είναι
είναι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες