Φυσικά δε φιλοδοξώ να παραστήσω τον Murray Klamkin, αλλά κάνω την αρχή με ένα τέτοιο και αν υπάρχει ενδιαφέρον ας το συνεχίσουμε.
1o Quickie
Αν
 να αποδείξετε ότι
να αποδείξετε ότι
Συντονιστής: spyros
 να αποδείξετε ότι
να αποδείξετε ότι
Μία αντιμετώπιση προς επαναφορά της άσκησης κυρίως αφού σίγουρα δεν βρήκα το κλειδί που τα "σπάει" , όπως λέει ο θεματοδότης και ΝΑΙ υπάρχει ενδιαφέρον και να συνεχιστούν αυτές οι προκλητικές και όμορφες ασκήσεις. Σκέψεις..matha έγραψε:Τα Quickies τα γνωρίζουμε από το Mathematics Magazine. Πρόκειται για προβλήματα τα οποία, αν και ίσως φαίνονται ορισμένες φορές δύσκολα ή φαίνεται ότι απαιτούν μακροσκελή απόδειξη, μπορούν να λυθούν μέσα σε δυο-τρεις γραμμές, αρκεί κανείς να βρει το κλειδί που τα "σπάει".
Φυσικά δε φιλοδοξώ να παραστήσω τον Murray Klamkin, αλλά κάνω την αρχή με ένα τέτοιο και αν υπάρχει ενδιαφέρον ας το συνεχίσουμε.
1o Quickie
Αννα αποδείξετε ότι
 και
και  .
. , θα ισχύει :
, θα ισχύει : . Ό,τι συμβαίνει λοιπόν στο
. Ό,τι συμβαίνει λοιπόν στο  , θα συμβαίνει και στο
, θα συμβαίνει και στο  . Ας δουλέψω μόνο στο
. Ας δουλέψω μόνο στο  .
.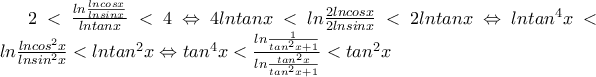
 ως
ως  , ποσότητα που βρίσκεται στο διάστημα
, ποσότητα που βρίσκεται στο διάστημα  και ισοδύναμα πάλι θέλω να αποδείξω ότι :
και ισοδύναμα πάλι θέλω να αποδείξω ότι :
 είναι
είναι 
 .
. η συνάρτηση
η συνάρτηση  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.
![\displaystyle \left[ {\left| {\ln \left( {\cos x} \right)} \right|,\;\left| {\ln \left( {\sin x} \right)} \right|} \right] \displaystyle \left[ {\left| {\ln \left( {\cos x} \right)} \right|,\;\left| {\ln \left( {\sin x} \right)} \right|} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/c8cd883f016e2f0f242404b6d1c12c66.png) η
η  είναι συνεχής και στο
είναι συνεχής και στο  παραγωγίσιμη, οπότε, από Θ.Μ.Τ., υπάρχει
παραγωγίσιμη, οπότε, από Θ.Μ.Τ., υπάρχει  τέτοιο ώστε
τέτοιο ώστε .
.


 .
.

Σκέψεις...matha έγραψε:... αρκεί κανείς να βρει το κλειδί που τα "σπάει".
1o Quickie
Αννα αποδείξετε ότι


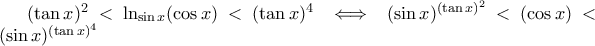

 , τη συνάρτηση
, τη συνάρτηση  . Εύκολα αποδεικνύουμε ότι η παράγωγος
. Εύκολα αποδεικνύουμε ότι η παράγωγος 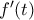 μηδενίζεται στο μοναδικό σημείο
μηδενίζεται στο μοναδικό σημείο  . Επίσης
. Επίσης  . Έτσι, το ζητούμενο έπεται από το θεώρημα Rolle.
. Έτσι, το ζητούμενο έπεται από το θεώρημα Rolle.dement έγραψε:Όπως εξήγησα στον Θάνο, αυτή η σχέση μού προέκυψε ενώ δούλευα πάνω στο άλλο ωραίο πρόβλημα που είχε στείλει (με την τριγωνομετρική ανισότητα).
Θεωρούμε, για δεδομένο, τη συνάρτηση
. Εύκολα αποδεικνύουμε ότι η παράγωγος
μηδενίζεται στο μοναδικό σημείο
. Επίσης
. Έτσι, το ζητούμενο έπεται από το θεώρημα Rolle.
dement έγραψε:Όπως εξήγησα στον Θάνο, αυτή η σχέση μού προέκυψε ενώ δούλευα πάνω στο άλλο ωραίο πρόβλημα που είχε στείλει (με την τριγωνομετρική ανισότητα).
Θεωρούμε, για δεδομένο, τη συνάρτηση
. Εύκολα αποδεικνύουμε ότι η παράγωγος
μηδενίζεται στο μοναδικό σημείο
. Επίσης
. Έτσι, το ζητούμενο έπεται από το θεώρημα Rolle.
Αυτή ακριβώς ήταν και η ιδέα κατασκευής του προβλήματος! Τόσο απλό, και συνάμα δύσκολο να το φανταστεί κανείς. (εκτός του Δημήτρη που το μυρίστηηκε αμέσως).dement έγραψε:Όπως εξήγησα στον Θάνο, αυτή η σχέση μού προέκυψε ενώ δούλευα πάνω στο άλλο ωραίο πρόβλημα που είχε στείλει (με την τριγωνομετρική ανισότητα).
Θεωρούμε, για δεδομένο, τη συνάρτηση
. Εύκολα αποδεικνύουμε ότι η παράγωγος
μηδενίζεται στο μοναδικό σημείο
. Επίσης
. Έτσι, το ζητούμενο έπεται από το θεώρημα Rolle.

Μπορώ να δείξω ότι ανήκει στοmatha έγραψε:Αυτή ακριβώς ήταν και η ιδέα κατασκευής του προβλήματος! Τόσο απλό, και συνάμα δύσκολο να το φανταστεί κανείς. (εκτός του Δημήτρη που το μυρίστηηκε αμέσως).dement έγραψε:Όπως εξήγησα στον Θάνο, αυτή η σχέση μού προέκυψε ενώ δούλευα πάνω στο άλλο ωραίο πρόβλημα που είχε στείλει (με την τριγωνομετρική ανισότητα).
Θεωρούμε, για δεδομένο, τη συνάρτηση
. Εύκολα αποδεικνύουμε ότι η παράγωγος
μηδενίζεται στο μοναδικό σημείο
. Επίσης
. Έτσι, το ζητούμενο έπεται από το θεώρημα Rolle.
Πάντως υπάρχει περιθώριο βελτίωσης. Ισχύει
όπως φαίνεται από την απόδειξη του Γιώργου Ρίζου.
 το οποίο είναι και βέλτιστο.
το οποίο είναι και βέλτιστο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 20 επισκέπτες