μιγαδικοί
Συντονιστής: nsmavrogiannis
Re: μιγαδικοί
Με την άδεια του Ροδόλφου θα παρακάμψω τους μιγαδικούς αφού έτσι το πρόβλημα γενικεύεται σε περισσότερες διαστάσεις.
Έστω το σύνολο των σημείων του χάρτη
το σύνολο των σημείων του χάρτη  και
και  η Ευκλείδεια μετρική. Ορίζουμε απεικόνιση
η Ευκλείδεια μετρική. Ορίζουμε απεικόνιση  τέτοια ώστε το
τέτοια ώστε το  να είναι το σημείο κάτω από το σημείο του χάρτη
να είναι το σημείο κάτω από το σημείο του χάρτη  που αντιστοιχεί στο
που αντιστοιχεί στο  . Εύκολα αποδεικνύεται ότι η
. Εύκολα αποδεικνύεται ότι η  είναι συνεχής.
είναι συνεχής.
Έστω τυχαίο . Ορίζουμε την ακολουθία
. Ορίζουμε την ακολουθία  με
με  . Αν η κλίμακα του χάρτη
. Αν η κλίμακα του χάρτη  ως προς τον
ως προς τον  είναι
είναι  τότε
τότε  . Έτσι
. Έτσι  για
για  και η
και η  είναι Cauchy, οπότε συγκλίνουσα. Έστω
είναι Cauchy, οπότε συγκλίνουσα. Έστω  . Λόγω συνέχειας της
. Λόγω συνέχειας της  ισχύει
ισχύει  και έτσι αποδείχθηκε η ύπαρξη.
και έτσι αποδείχθηκε η ύπαρξη.
Για τη μοναδικότητα, έστω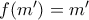 . Ισχύει
. Ισχύει  .
.
Έστω
 το σύνολο των σημείων του χάρτη
το σύνολο των σημείων του χάρτη  και
και  η Ευκλείδεια μετρική. Ορίζουμε απεικόνιση
η Ευκλείδεια μετρική. Ορίζουμε απεικόνιση  τέτοια ώστε το
τέτοια ώστε το  να είναι το σημείο κάτω από το σημείο του χάρτη
να είναι το σημείο κάτω από το σημείο του χάρτη  που αντιστοιχεί στο
που αντιστοιχεί στο  . Εύκολα αποδεικνύεται ότι η
. Εύκολα αποδεικνύεται ότι η  είναι συνεχής.
είναι συνεχής.Έστω τυχαίο
 . Ορίζουμε την ακολουθία
. Ορίζουμε την ακολουθία  με
με  . Αν η κλίμακα του χάρτη
. Αν η κλίμακα του χάρτη  ως προς τον
ως προς τον  είναι
είναι  τότε
τότε  . Έτσι
. Έτσι  για
για  και η
και η  είναι Cauchy, οπότε συγκλίνουσα. Έστω
είναι Cauchy, οπότε συγκλίνουσα. Έστω  . Λόγω συνέχειας της
. Λόγω συνέχειας της  ισχύει
ισχύει  και έτσι αποδείχθηκε η ύπαρξη.
και έτσι αποδείχθηκε η ύπαρξη.Για τη μοναδικότητα, έστω
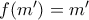 . Ισχύει
. Ισχύει  .
.Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Re: μιγαδικοί
πράγματι πρόκειται για πρόβλημα σταθερού σημείου σε...
αν επιμείνω στους μιγαδικούς
μεταφερω το Β(ΑΒCD) κατά το διάνυσμα ΑΑ΄ τότε ο γίνεται
γίνεται 
στρέφω τον Β κατά γωνία θ γύρω από την κορυφή Α΄ του Α(Α΄Β΄C΄D΄)ώστε το Β να βρεθεί στην Α΄Β΄τοτε ο γίνεται
γίνεται 
Μεγενθύνω τον κατά την αναλογία του λόγου των πλευρών
κατά την αναλογία του λόγου των πλευρών  o
o  γίνεται
γίνεται  .
.
Θελουμε ο Α να ταυτιστεί με τον Β ή όμως
όμως  .αρα
.αρα  ή
ή 
H εξίσωση είναι 1 ου βαθμου , με αφου
αφου  επομένως έχει ακριβώς μια λύση
επομένως έχει ακριβώς μια λύση
αν επιμείνω στους μιγαδικούς
μεταφερω το Β(ΑΒCD) κατά το διάνυσμα ΑΑ΄ τότε ο
 γίνεται
γίνεται 
στρέφω τον Β κατά γωνία θ γύρω από την κορυφή Α΄ του Α(Α΄Β΄C΄D΄)ώστε το Β να βρεθεί στην Α΄Β΄τοτε ο
 γίνεται
γίνεται 
Μεγενθύνω τον
 κατά την αναλογία του λόγου των πλευρών
κατά την αναλογία του λόγου των πλευρών  o
o  γίνεται
γίνεται  .
.Θελουμε ο Α να ταυτιστεί με τον Β ή
 όμως
όμως  .αρα
.αρα  ή
ή 
H εξίσωση είναι 1 ου βαθμου , με
 αφου
αφου  επομένως έχει ακριβώς μια λύση
επομένως έχει ακριβώς μια λύσηΜέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
