'Εστω
 και
και 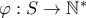 με
με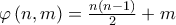 .
.Να αποδειχθεί ότι η
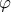 είναι 1-1 και επί.
είναι 1-1 και επί.Συντονιστής: nsmavrogiannis
 και
και 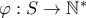 με
με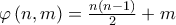 .
.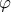 είναι 1-1 και επί.
είναι 1-1 και επί.Θυμίζει το επιχείρημα Cantor.nsmavrogiannis έγραψε: ↑Κυρ Νοέμ 21, 2021 12:26 amΔεν είνα άγνωστη. Αλλά είναι ενδιαφέρουσα.
'Εστωκαι
με
.
Να αποδειχθεί ότι ηείναι 1-1 και επί.
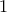
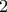
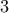
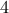 ....
.... 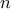 (κόκκινη γραμματοσειρά) πηγαίνοντας από πάνω δεξιά προς τα κάτω αριστερά.
(κόκκινη γραμματοσειρά) πηγαίνοντας από πάνω δεξιά προς τα κάτω αριστερά.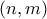 βρίσκεται εκ κατασκευής στην
βρίσκεται εκ κατασκευής στην  κόκκινη γραμμή και μάλιστα
κόκκινη γραμμή και μάλιστα  θέσεις κάτω. 'Αρα α) προηγούνται οι
θέσεις κάτω. 'Αρα α) προηγούνται οι 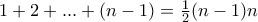 αριθμοί στις προηγούμενες
αριθμοί στις προηγούμενες  κόκκινες γραμμές, β) ο ίδιος είναι
κόκκινες γραμμές, β) ο ίδιος είναι 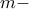 οστός στην γραμμή του. Άρα η αρίθμηση του
οστός στην γραμμή του. Άρα η αρίθμηση του 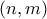 στην διάταξη είναι
στην διάταξη είναι 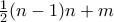 .
.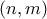 με
με 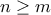 έχει απαριθμηθεί, και μάλιστα ακριβώς μία φορά. Με άλλα λόγια η απεικόνιση
έχει απαριθμηθεί, και μάλιστα ακριβώς μία φορά. Με άλλα λόγια η απεικόνιση 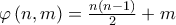 είναι α) επί (αφού η απαρίθμηση είναι
είναι α) επί (αφού η απαρίθμηση είναι 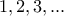 χωρίς να λείπει κανείς) και β)
χωρίς να λείπει κανείς) και β)  αφού κάθε ζεύγος
αφού κάθε ζεύγος 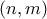 με
με 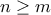 είναι σε άλλη θέση στην απαρίθμηση.
είναι σε άλλη θέση στην απαρίθμηση.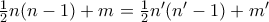 όπου
όπου  και
και 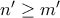 . Θα δείξουμε ότι
. Θα δείξουμε ότι 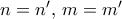 (αυτο είναι το
(αυτο είναι το  .
.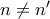 θα ήταν χωρίς βλάβη
θα ήταν χωρίς βλάβη 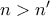 , οπότε και
, οπότε και 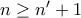 . Aλλά τότε
. Aλλά τότε 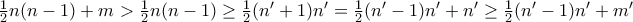 , που αντιβαίνει στην υπόθεση.
, που αντιβαίνει στην υπόθεση.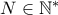 . Ο
. Ο  αυτός βρίσκεται σε κάποιο από τα διαδοχικά διαστήματα
αυτός βρίσκεται σε κάποιο από τα διαδοχικά διαστήματα ![(0,\, 1], \, (1,\, 1+2], \, (1+2,\, 1+2+3] ,\, ... (0,\, 1], \, (1,\, 1+2], \, (1+2,\, 1+2+3] ,\, ...](/forum/ext/geomar/texintegr/latexrender/pictures/d2481d7ad17d49b471b5521f65cceb3c.png) . Έστω στο
. Έστω στο ![(1+2+...+n-1,\, 1+2+...+n] (1+2+...+n-1,\, 1+2+...+n]](/forum/ext/geomar/texintegr/latexrender/pictures/fac730e0e796aec2fb102a2424889695.png) , δηλαδή ισχύει
, δηλαδή ισχύει 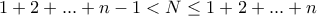 . Είναι λοιπόν
. Είναι λοιπόν  . Θέτουμε
. Θέτουμε 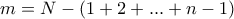 , οπότε
, οπότε 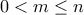 και βέβαια
και βέβαια 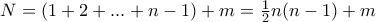 , όπως θέλαμε.
, όπως θέλαμε.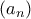 μια γνησίως αύξουσα ακολουθία φυσικών αριθμών με
μια γνησίως αύξουσα ακολουθία φυσικών αριθμών με 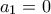 . Προφανώς
. Προφανώς 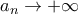 και η κλάση διαστημάτων
και η κλάση διαστημάτων ![(a_{n},a_{n+1}] (a_{n},a_{n+1}]](/forum/ext/geomar/texintegr/latexrender/pictures/14372d4f3189ba9d52478a8321ff7824.png) αποτελεί διαμέριση του
αποτελεί διαμέριση του 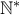 . Κάθε θετικός ακέραιος
. Κάθε θετικός ακέραιος  γράφεται κατά μοναδικό τρόπο
γράφεται κατά μοναδικό τρόπο 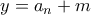 όπου
όπου 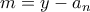 και επομένως
και επομένως 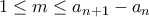 . Αν πάρουμε
. Αν πάρουμε 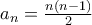 έχουμε
έχουμε 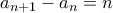 και επομένως για κάθε θετικό ακέραιο
και επομένως για κάθε θετικό ακέραιο  υπάρχουν μοναδικοί θετικοί ακέραιοι
υπάρχουν μοναδικοί θετικοί ακέραιοι  και
και 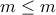 ώστε
ώστε 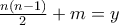 που αποδεικνύει το ζητούμενο.
που αποδεικνύει το ζητούμενο.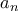 βρίσκουμε αμφεικονίσεις διαφόρων υποσυνόλων του
βρίσκουμε αμφεικονίσεις διαφόρων υποσυνόλων του  επί του
επί του 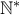 .
.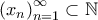 , όπου
, όπου 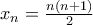 .Είναι προφανές ότι η ακολουθία αυτή είναι γνησίως αύξουσα. Για
.Είναι προφανές ότι η ακολουθία αυτή είναι γνησίως αύξουσα. Για 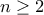 ορίζουμε
ορίζουμε 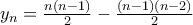 .
. 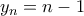 , που σημαίνει ότι η διαφορά μεταξύ δύο διαδοχικών όρων της ακολουθίας
, που σημαίνει ότι η διαφορά μεταξύ δύο διαδοχικών όρων της ακολουθίας  δεν είναι άνω φραγμένη.
δεν είναι άνω φραγμένη.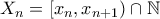
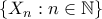 ορίζει μια διαμέριση του
ορίζει μια διαμέριση του  , για την οποία κάθε μέλος της διαμέρισης είναι πεπερασμένα αριθμήσιμο, και η ακολουθία
, για την οποία κάθε μέλος της διαμέρισης είναι πεπερασμένα αριθμήσιμο, και η ακολουθία 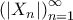 είναι μια γνησίως αύξουσα ακολουθία φυσικών αριθμών, με
είναι μια γνησίως αύξουσα ακολουθία φυσικών αριθμών, με 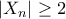 για κάθε
για κάθε 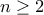 . Θεωρούμε τώρα
. Θεωρούμε τώρα 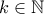 τυχόν. Θα διακρίνουμε τις ακόλουθες περιπτώσεις.
τυχόν. Θα διακρίνουμε τις ακόλουθες περιπτώσεις.
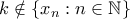 . Τότε, υπάρχει φυσικός αριθμός
. Τότε, υπάρχει φυσικός αριθμός 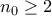 τέτοιο ώστε
τέτοιο ώστε 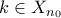 . Από γνωστές ιδιότητες της διαμέρισης
. Από γνωστές ιδιότητες της διαμέρισης 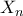 έχουμε ότι η απόσταση του
έχουμε ότι η απόσταση του  από το
από το 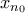 είναι ένας μη μηδενικός φυσικός αριθμός, ο οποίος είναι μικρότερος του
είναι ένας μη μηδενικός φυσικός αριθμός, ο οποίος είναι μικρότερος του 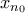 (προκύπτει άμεσα ως ιδιότητα της ακολουθίας
(προκύπτει άμεσα ως ιδιότητα της ακολουθίας 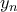 που ορίσαμε προηγουμένως). Αν είναι
που ορίσαμε προηγουμένως). Αν είναι  η απόσταση αυτή. 'Εχουμε λοιπόν ότι
η απόσταση αυτή. 'Εχουμε λοιπόν ότι 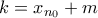 όπου
όπου 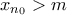 . Άρα
. Άρα 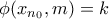 .
.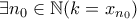 . Στην περίπτωση όπου
. Στην περίπτωση όπου 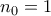 είναι προφανές ότι
είναι προφανές ότι 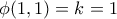 . Ας υποθέσουμε λοιπόν, για την αποφυγή τετριμμένων καταστάσεων, ότι
. Ας υποθέσουμε λοιπόν, για την αποφυγή τετριμμένων καταστάσεων, ότι 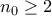 . Τότε, σύμφωνα με τον ορσιμό της ακολουθίας
. Τότε, σύμφωνα με τον ορσιμό της ακολουθίας 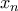 έχουμε ότι
έχουμε ότι 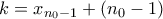 , όπου όπως επισημάναμε στη προηγούμενη περίπτωση έχουμε ότι
, όπου όπως επισημάναμε στη προηγούμενη περίπτωση έχουμε ότι 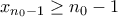 . Άρα
. Άρα 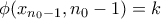 .
.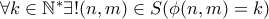
 είναι αμφιμονοσήμαντη.
είναι αμφιμονοσήμαντη.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες