1.
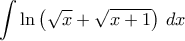
2.
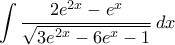
3.
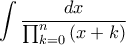
4.
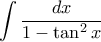
και ένα πιο δύσκολο το οποίο ξεφεύγει αρκετά από τα παραπάνω:
5.
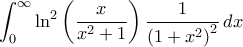
Συντονιστής: emouroukos
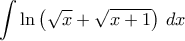
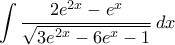
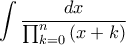
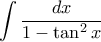
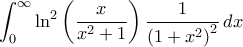

Ολοκληρώνουμε στο διάστημαTolaso J Kos έγραψε:Μέρα που είναι ας κεράσω και ολοκληρώματα. Ας υπολογιστούν τα παρακάτω:
1.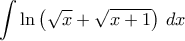
 . Με ολοκλήρωση κατά παράγοντες έχουμε :
. Με ολοκλήρωση κατά παράγοντες έχουμε :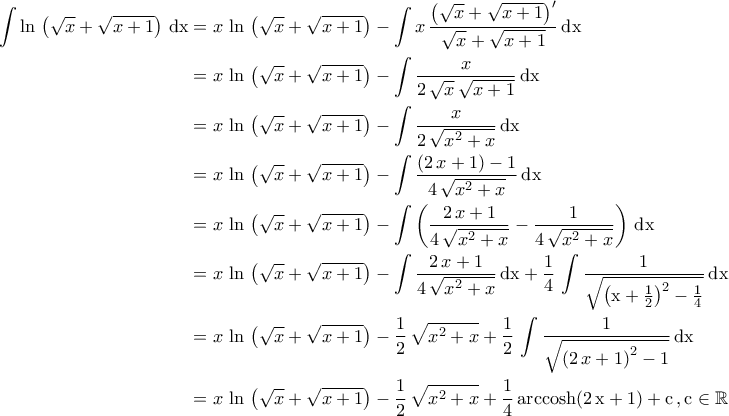

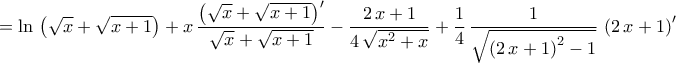
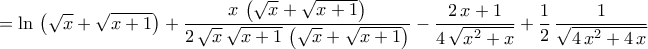

 .
.ΓιαTolaso J Kos έγραψε: 2.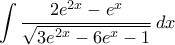
 έχουμε :
έχουμε : .
. , το διάστημα ολοκλήρωσης είναι το
, το διάστημα ολοκλήρωσης είναι το  .
.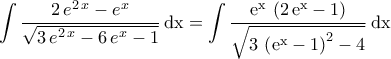
 , έχουμε
, έχουμε  και
και  , οπότε :
, οπότε :
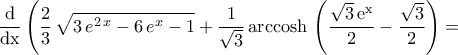
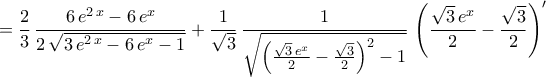
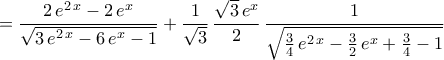
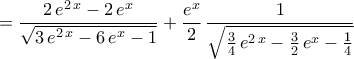

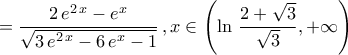
ΈστωTolaso J Kos έγραψε: 3.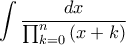
 .
. είτε στο
είτε στο  είτε... είτε στο
είτε... είτε στο  .
. για τις οποίες ισχύει ότι
για τις οποίες ισχύει ότι

 παίρνουμε
παίρνουμε 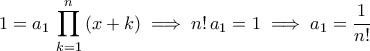
 παίρνουμε
παίρνουμε 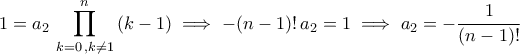
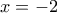 παίρνουμε
παίρνουμε 
 και βλέπουμε ότι
και βλέπουμε ότι 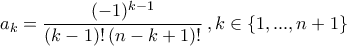
 και άρα είναι οι μοναδικοί με αυτήν την ιδιότητα) , οπότε
και άρα είναι οι μοναδικοί με αυτήν την ιδιότητα) , οπότε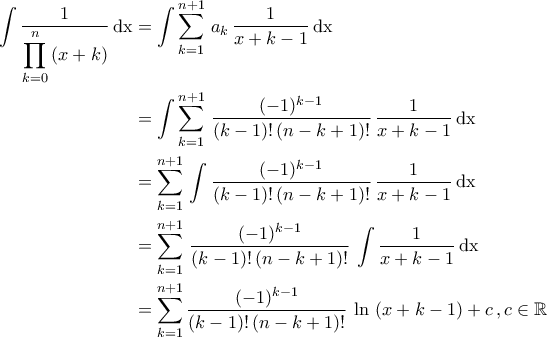
 .
. , τότε :
, τότε :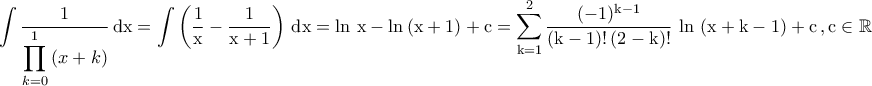
 , τότε :
, τότε :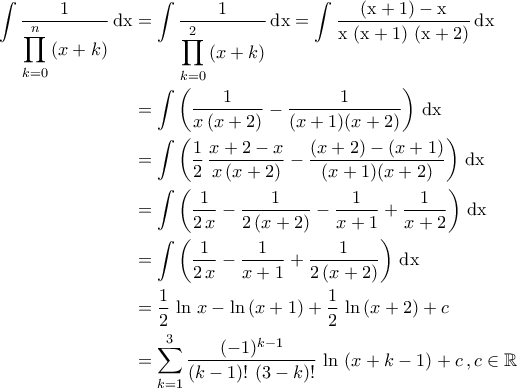
Μια λύση:Tolaso J Kos έγραψε:...και ένα πιο δύσκολο το οποίο ξεφεύγει αρκετά από τα παραπάνω:
5.
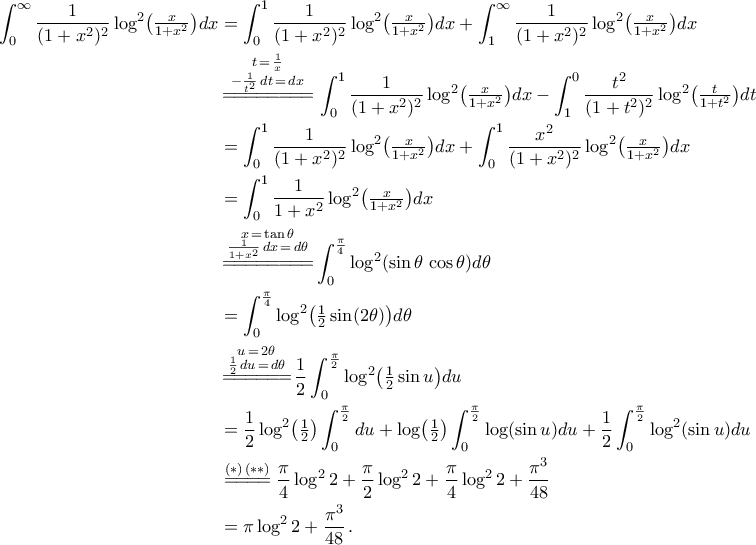
 (Εύκολο.)
(Εύκολο.) (Αφήνεται προς το παρόν σαν άσκηση.)
(Αφήνεται προς το παρόν σαν άσκηση.)
Πάμε κατευθείαν στο δεύτερο ολοκλήρωμα, και λίγο συνοπτικά γιατί πρέπει να φύγω.grigkost έγραψε: Χρησιμοποιήθηκαν:
(Εύκολο.)
(Αφήνεται προς το παρόν σαν άσκηση.)
 δίνει άμεσα αποτέλεσμα, για όποιον δεν τον έχει ξανά δει.
δίνει άμεσα αποτέλεσμα, για όποιον δεν τον έχει ξανά δει. με παράγωγιση δύο φορές. Εδώ θα δώσω έναν άλλο τρόπο που έχω δει για αυτό σε ένα βιβλίο και χρησιμοποιεί σειρές
με παράγωγιση δύο φορές. Εδώ θα δώσω έναν άλλο τρόπο που έχω δει για αυτό σε ένα βιβλίο και χρησιμοποιεί σειρές  .
. . Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:
. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε: 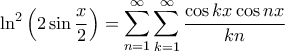
 ως
ως  και θα χουμε λοιπόν:
και θα χουμε λοιπόν:  .
. αφού
αφού  .
.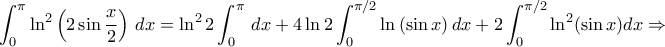


Ολοκληρώνουμε είτε στοTolaso J Kos έγραψε: 4.
 είτε στο
είτε στο  ή στο
ή στο  .
.![\displaystyle{\begin{aligned} \int \dfrac{1}{1-\tan^2\,x}\,\rm{dx}&=\int \dfrac{\cos^2\,x}{\cos^2\,x-\sin^2\,x}\,\rm{dx}\\&=\int \dfrac{\cos\,(2\,x)+1}{2\,\cos\,(2\,x)}\,\rm{dx}\\&=\int \left(\dfrac{1}{2\,\cos\,2\,x}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left(\dfrac{\cos\,2\,x}{2\,\left(1-\sin^2\,2\,x\right)}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left[\frac{\cos\,2\,x}{4}\,\dfrac{\left(1+\sin\,2\,x\right)+\left(1-\sin\,2\,x\right)}{\left(1-\sin\,2\,x\right)\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\int \left[\dfrac{2\,\cos\,2\,x}{8\,\left(1-\sin\,2\,x\right)}+\dfrac{2\,\cos\,2\,x}{8\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\frac{1}{8}\,\ln\,\left|1+\sin\,2\,x\right|-\frac{1}{8}\,\ln\,\left|1-\sin\,2\,x\right|+\frac{x}{2}+c\,,c\in\mathbb{R}\end{aligned}} \displaystyle{\begin{aligned} \int \dfrac{1}{1-\tan^2\,x}\,\rm{dx}&=\int \dfrac{\cos^2\,x}{\cos^2\,x-\sin^2\,x}\,\rm{dx}\\&=\int \dfrac{\cos\,(2\,x)+1}{2\,\cos\,(2\,x)}\,\rm{dx}\\&=\int \left(\dfrac{1}{2\,\cos\,2\,x}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left(\dfrac{\cos\,2\,x}{2\,\left(1-\sin^2\,2\,x\right)}+\frac{1}{2}\right)\,\rm{dx}\\&=\int \left[\frac{\cos\,2\,x}{4}\,\dfrac{\left(1+\sin\,2\,x\right)+\left(1-\sin\,2\,x\right)}{\left(1-\sin\,2\,x\right)\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\int \left[\dfrac{2\,\cos\,2\,x}{8\,\left(1-\sin\,2\,x\right)}+\dfrac{2\,\cos\,2\,x}{8\,\left(1+\sin\,2\,x\right)}+\frac{1}{2}\right]\,\rm{dx}\\&=\frac{1}{8}\,\ln\,\left|1+\sin\,2\,x\right|-\frac{1}{8}\,\ln\,\left|1-\sin\,2\,x\right|+\frac{x}{2}+c\,,c\in\mathbb{R}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/55e3450c89a367054b90b6a9902833f2.png)
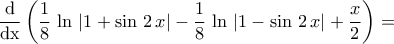


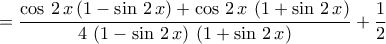
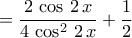
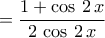
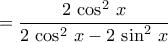

Μια σπουδαία σχέση (αρκετά γενικότερη) είναι : ΓιαTolaso J Kos έγραψε:
Υ.Σ Υπάρχει λύση και με μιγαδική ανάλυση. Δε τη βρίσκω αυτή τη στιγμή να την ανεβάσω. Όποιος θέλει ας το κάνει.
 ισχύει
ισχύει  .
.  είναι αναλυτική στον ανοιχτό δίσκο
είναι αναλυτική στον ανοιχτό δίσκο  (διότι
(διότι  ), επομένως
), επομένως  κι επειδή
κι επειδή  , θα ισχύει
, θα ισχύει  . Άρα ..
. Άρα ..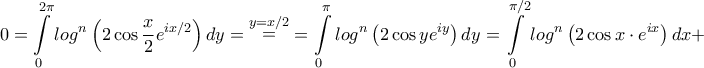
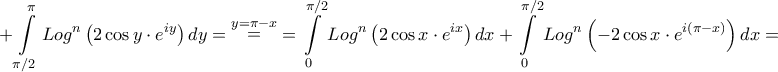
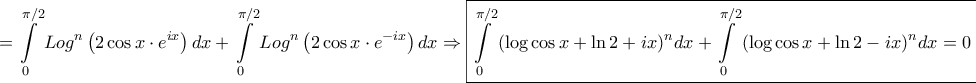
 και για
και για  πρκύπτει το ζητούμενο. "Παίζοντας" με το
πρκύπτει το ζητούμενο. "Παίζοντας" με το  προκύπτουν κι άλλες σχέσεις.
προκύπτουν κι άλλες σχέσεις.Εδώ χρησιμοποιήθηκε ότιTolaso J Kos έγραψε:Έχουμε ότι:. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:
 .
.Πώς δικαιολογείται παραπάνω η αλλαγή ολοκλήρωσης και αθροίσεων;Tolaso J Kos έγραψε:Τώρα το δεξί μέλος κάνει:αφού
.
Πρόκειται για γνωστή (?) πρόταση, την οποία όμως δεν την έχω δει σε κανένα βιβλίο γραμμένη. Έχουν χρησιμοποιηθεί και αρκετές φορές στοΚοτρώνης Αναστάσιος έγραψε:Εδώ χρησιμοποιήθηκε ότιTolaso J Kos έγραψε:Έχουμε ότι:. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:
.
Γιατί ισχύει αυτό;
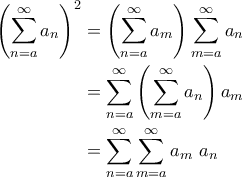
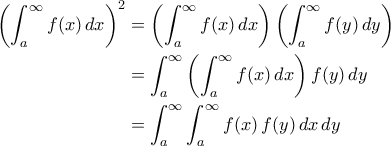
 ( δε γνωρίζω αν
( δε γνωρίζω αν  και στις σειρές)
και στις σειρές) .
.
 οπότε και τη ζητούμενη τιμή του
οπότε και τη ζητούμενη τιμή του  .
.
Καλησπέρα.Tolaso J Kos έγραψε:Πρόκειται για γνωστή (?) πρόταση, την οποία όμως δεν την έχω δει σε κανένα βιβλίο γραμμένη. Έχουν χρησιμοποιηθεί και αρκετές φορές στοΚοτρώνης Αναστάσιος έγραψε:Εδώ χρησιμοποιήθηκε ότιTolaso J Kos έγραψε:Έχουμε ότι:. Παίρνουμε τετράγωνα και στα δύο μέλη και έχουμε:
.
Γιατί ισχύει αυτό;, σε υπολογισμούς σειρών (πρόσφατα μάλιστα).
Μία απόδειξη που γνωρίζω είναι η παρακάτω:
Ίδια λογική ισχύει και για τα ολοκληρώματα, δηλ:
όπου( δε γνωρίζω αν
και στις σειρές)
Η τελευταία ιδιότητα (δηλ. των ολοκληρωμάτων) χρησιμοποιείται σε μία από τις πολλές αποδείξεις του.
Δηλαδή έστω
Και στη συνέχεια προχωράμε με αλλαγή συντεταγμένων σε πολικές, για να πάρουμε τελικά ότιοπότε και τη ζητούμενη τιμή του
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης