θεωρίας μέτρου τις οποίες παραθέτω για τους λάτρεις του ''αθλήματος''.
(1) Έστω
 μετρήσιμο με
μετρήσιμο με 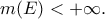
(i) Δείξτε ότι η συνάρτηση
 με τύπο
με τύπο ![\displaystyle{f(x)=m(E\cap[-x,x])} \displaystyle{f(x)=m(E\cap[-x,x])}](/forum/ext/geomar/texintegr/latexrender/pictures/8caaff9607f76ea34961009ad41a4ce3.png) είναι συνεχής.
είναι συνεχής.(ii) Aν
 δείξτε ότι υπάρχει
δείξτε ότι υπάρχει  μετρήσιμο τέτοιο ώστε
μετρήσιμο τέτοιο ώστε 
(2) Έστω
 ολοκληρώσιμη συνάρτηση. Δείξτε ότι:
ολοκληρώσιμη συνάρτηση. Δείξτε ότι:
Συντονιστής: emouroukos
 μετρήσιμο με
μετρήσιμο με 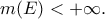
 με τύπο
με τύπο ![\displaystyle{f(x)=m(E\cap[-x,x])} \displaystyle{f(x)=m(E\cap[-x,x])}](/forum/ext/geomar/texintegr/latexrender/pictures/8caaff9607f76ea34961009ad41a4ce3.png) είναι συνεχής.
είναι συνεχής. δείξτε ότι υπάρχει
δείξτε ότι υπάρχει  μετρήσιμο τέτοιο ώστε
μετρήσιμο τέτοιο ώστε 
 ολοκληρώσιμη συνάρτηση. Δείξτε ότι:
ολοκληρώσιμη συνάρτηση. Δείξτε ότι:

![[-y,y]\cap E=([-x,x]\cap E)\cup ([x,y]\cap E)\cup ([-y,-x]\cap E) [-y,y]\cap E=([-x,x]\cap E)\cup ([x,y]\cap E)\cup ([-y,-x]\cap E)](/forum/ext/geomar/texintegr/latexrender/pictures/15fc67d5f87068640f1e4d7f5db77fc8.png)
![m(E\cap [x,y]),m(E\cap [-y,-x])\leq y-x m(E\cap [x,y]),m(E\cap [-y,-x])\leq y-x](/forum/ext/geomar/texintegr/latexrender/pictures/d118f25eaf614220ecbc96d3e0bbd537.png)



 (0)
(0)
 ώστε
ώστε 

 (1)
(1)

 (2)
(2) συμπεραίνουμε ότι
συμπεραίνουμε ότι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες