 παραγωγίσιμη
παραγωγίσιμη  ανοικτό διάστημα και
ανοικτό διάστημα και 
Εστω
 συνεχής.
συνεχής.Ισχύει ότι

Αν

τότε η εξίσωση
 δεν έχει ρίζα στο
δεν έχει ρίζα στο 
Συντονιστής: emouroukos
 παραγωγίσιμη
παραγωγίσιμη  ανοικτό διάστημα και
ανοικτό διάστημα και 
 συνεχής.
συνεχής.

 δεν έχει ρίζα στο
δεν έχει ρίζα στο 
 είναι παραγωγίσιμη, είναι και συνεχής. Άρα και η συνάρτηση
είναι παραγωγίσιμη, είναι και συνεχής. Άρα και η συνάρτηση  είναι συνεχής.
είναι συνεχής.  ως
ως
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  για κάθε
για κάθε  .
. η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο  με
με![\displaystyle{ k'(x) = \cdots = e^{-h(x)}\left[f'(x) - f(x)g(f(x)+x) \right] = 0} \displaystyle{ k'(x) = \cdots = e^{-h(x)}\left[f'(x) - f(x)g(f(x)+x) \right] = 0}](/forum/ext/geomar/texintegr/latexrender/pictures/a8eb03f163d598efdab2c3470d0c2e8a.png)
 είναι σταθερή στο
είναι σταθερή στο  . Επειδή
. Επειδή  , τότε
, τότε  για κάθε
για κάθε  . Άρα και
. Άρα και  για κάθε
για κάθε  όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε. για κάθε
για κάθε  αλλά δεν χρειαζόταν για το επιχείρημα.]
αλλά δεν χρειαζόταν για το επιχείρημα.] που ανήκει στο
που ανήκει στο  ώστε
ώστε 
 που ανήκει στο
που ανήκει στο 





Κάμποσα. Π.χ.mikemoke έγραψε:Υπάρχουν λάθη στον παραπάνω συλλογισμό ;
Δεν μπορούμε να απλοποιήσουμε τοmikemoke έγραψε: Άρα
 .
. Το αριστερό όριο είναι εσφαλμένο και δεν βλέπω πώς βγήκε το δεξί.mikemoke έγραψε:
ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
 με
με  ώστε
ώστε  (πρώτη ρίζα μετά το
(πρώτη ρίζα μετά το  ) ,ακόμα προκύπτει
) ,ακόμα προκύπτει 
 με
με 
 ώστε f κυρτή , f(x)>0 και f'(x)<0
ώστε f κυρτή , f(x)>0 και f'(x)<0![x\in[k,t] x\in[k,t]](/forum/ext/geomar/texintegr/latexrender/pictures/09a1b64a69c00e1ae565043f3a468ce1.png) ισχύει
ισχύει 




Φαντάζομαι εννοείς «πρώτη ρίζα μετά τοmikemoke έγραψε:ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
με
ώστε
(πρώτη ρίζα μετά το
)
 ». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της
». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της  .
. και όχι αυτήν που έγραψα.
και όχι αυτήν που έγραψα.Γιατί δεν μπορούμε να το πούμε ;Demetres έγραψε:Φαντάζομαι εννοείς «πρώτη ρίζα μετά τοmikemoke έγραψε:ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
με
ώστε
(πρώτη ρίζα μετά το
)
». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της
.
Εκ παραδρομής έδωσα λανθασμένο παράδειγμα. Δες το γράφημα τηςmikemoke έγραψε: Γιατί δεν μπορούμε να το πούμε ;
 . Υπάρχουν θετικές τιμές του
. Υπάρχουν θετικές τιμές του  στις οποίες μηδενίζεται αλλά δεν υπάρχει μικρότερη τέτοια.
στις οποίες μηδενίζεται αλλά δεν υπάρχει μικρότερη τέτοια.Δεν κατάλαβα .μηδενιζεται τι ; και το τέτοια τι σημαίνειDemetres έγραψε:Εκ παραδρομής έδωσα λανθασμένο παράδειγμα. Δες το γράφημα τηςmikemoke έγραψε: Γιατί δεν μπορούμε να το πούμε ;. Υπάρχουν θετικές τιμές του
στις οποίες μηδενίζεται αλλά δεν υπάρχει μικρότερη τέτοια.
 δεν υπάρχει μικρότερη.
δεν υπάρχει μικρότερη.Δημήτρη αυτό από ότι βλέπω είναι το μόνο σωστό από αυτά που γράφει mikemoke.Demetres έγραψε:Φαντάζομαι εννοείς «πρώτη ρίζα μετά τοmikemoke έγραψε:ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
με
ώστε
(πρώτη ρίζα μετά το
)
». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της
.
Επεξεργασία: Εννοούσα βέβαια την συνάρτησηκαι όχι αυτήν που έγραψα.
 και επειδή η
και επειδή η  είναι συνεχής
είναι συνεχής  και
και 
 εκτός ότι είναι συνεχής.
εκτός ότι είναι συνεχής.Γνωρίζουμε και ότι f'(t)=0 αφού η g είναι συνεχής και άρα για t δίνει πεπερασμένη τιμή και από κει βγάζω τηνΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Demetres έγραψε:Δημήτρη αυτό από ότι βλέπω είναι το μόνο σωστό από αυτά που γράφει mikemoke.mikemoke έγραψε:ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
με
ώστε
(πρώτη ρίζα μετά το
) [/quote
Φαντάζομαι εννοείς «πρώτη ρίζα μετά το». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της
.
Επεξεργασία: Εννοούσα βέβαια την συνάρτησηκαι όχι αυτήν που έγραψα.
και επειδή η
είναι συνεχής
και
π.χ το
Yπάρχει διάστημα [k,t) ώστε f κυρτή , f(x)>0 και f'(x)<0
δεν είναι σωστό γιατί δεν γνωρίζουμε τίποτα για τηνεκτός ότι είναι συνεχής.
 είναι κοίλη τότε αφού f(t)=0 και f'(t)=0 προκύπτει ότι f(x) < 0 άτοπο
είναι κοίλη τότε αφού f(t)=0 και f'(t)=0 προκύπτει ότι f(x) < 0 άτοπο  είναι τέτοιο ώστε η f να είναι είτε κοίλη είτε κυρτή
είναι τέτοιο ώστε η f να είναι είτε κοίλη είτε κυρτήΗmikemoke έγραψε:Γνωρίζουμε και ότι f'(t)=0 αφού η g είναι συνεχής και άρα για t δίνει πεπερασμένη τιμή και από κει βγάζω τηνΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Demetres έγραψε:Δημήτρη αυτό από ότι βλέπω είναι το μόνο σωστό από αυτά που γράφει mikemoke.mikemoke έγραψε:ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
με
ώστε
(πρώτη ρίζα μετά το
) [/quote
Φαντάζομαι εννοείς «πρώτη ρίζα μετά το». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της
.
Επεξεργασία: Εννοούσα βέβαια την συνάρτησηκαι όχι αυτήν που έγραψα.
και επειδή η
είναι συνεχής
και
π.χ το
Yπάρχει διάστημα [k,t) ώστε f κυρτή , f(x)>0 και f'(x)<0
δεν είναι σωστό γιατί δεν γνωρίζουμε τίποτα για τηνεκτός ότι είναι συνεχής.
κυρτότητα κτλ κοντά στο t.Τωρα αν στοείναι κοίλη τότε αφού f(t)=0 και f'(t)=0 προκύπτει ότι f(x) < 0 άτοπο
Να σημειωσω ότι το διάστημαείναι τέτοιο ώστε η f να είναι είτε κοίλη είτε κυρτή
 στο
στο  παίρνει μια συγκεκριμένη τιμή.Μπορεί όμως να υπάρχει
παίρνει μια συγκεκριμένη τιμή.Μπορεί όμως να υπάρχει 
 τότε όλα αυτά που γράφεις δεν ισχύουν.
τότε όλα αυτά που γράφεις δεν ισχύουν.Αν καταλαβαίνω καλά Μπορει στοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Ηmikemoke έγραψε:Γνωρίζουμε και ότι f'(t)=0 αφού η g είναι συνεχής και άρα για t δίνει πεπερασμένη τιμή και από κει βγάζω τηνΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Demetres έγραψε:Δημήτρη αυτό από ότι βλέπω είναι το μόνο σωστό από αυτά που γράφει mikemoke.mikemoke έγραψε:ΈστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο
με
ώστε
(πρώτη ρίζα μετά το
) [/quote
Φαντάζομαι εννοείς «πρώτη ρίζα μετά το». Δεν μπορούμε όμως να πούμε κάτι τέτοιο. (Δες για παράδειγμα το γράφημα της
.
Επεξεργασία: Εννοούσα βέβαια την συνάρτησηκαι όχι αυτήν που έγραψα.
και επειδή η
είναι συνεχής
και
π.χ το
Yπάρχει διάστημα [k,t) ώστε f κυρτή , f(x)>0 και f'(x)<0
δεν είναι σωστό γιατί δεν γνωρίζουμε τίποτα για τηνεκτός ότι είναι συνεχής.
κυρτότητα κτλ κοντά στο t.Τωρα αν στοείναι κοίλη τότε αφού f(t)=0 και f'(t)=0 προκύπτει ότι f(x) < 0 άτοπο
Να σημειωσω ότι το διάστημαείναι τέτοιο ώστε η f να είναι είτε κοίλη είτε κυρτή
στο
παίρνει μια συγκεκριμένη τιμή.Μπορεί όμως να υπάρχει
μετότε όλα αυτά που γράφεις δεν ισχύουν.
Να σημειώσω ότι το θέμα είναι πολύ πιό βαθύ από ότι φαίνεται.
 να αλλάζει μονοτονία ή και κυρτότητα άπειρες φορές και έτσι δεν μπορώ να ισχυριστώ τα παραπάνω μόνο με τα δεδομένα (f(t)=0,f'(t)=0).Δεν θα ισχύει όμως κατι τέτοιο αν το διάστημα γινόταν απειροστό ;
να αλλάζει μονοτονία ή και κυρτότητα άπειρες φορές και έτσι δεν μπορώ να ισχυριστώ τα παραπάνω μόνο με τα δεδομένα (f(t)=0,f'(t)=0).Δεν θα ισχύει όμως κατι τέτοιο αν το διάστημα γινόταν απειροστό ;Δεν υπάρχει τέτοια έννοια στα κλασσικά Μαθηματικά.mikemoke έγραψε: αν το διάστημα γινόταν απειροστό ;
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Σεπ 09, 2016 11:54 amΕστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο

 και
και  συνεχής άρα δεν παρουσιάζει συσσώρευση ριζών στο
συνεχής άρα δεν παρουσιάζει συσσώρευση ριζών στο  .Έστω ότι υπάρχει πρώτη ρίζα μετα το
.Έστω ότι υπάρχει πρώτη ρίζα μετα το  ,
,  ,
,
 .
. συνεχής
συνεχής 
 με
με  και
και 
 και
και  .
.


 συνεχής
συνεχής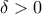
 με
με 
 με
με 
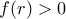
Αρα θα υπάρχουν ακολουθίεςmikemoke έγραψε: ↑Πέμ Φεβ 01, 2018 1:43 pmΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Σεπ 09, 2016 11:54 amΕστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο

και
συνεχής άρα δεν παρουσιάζει συσσώρευση ριζών στο
.Έστω ότι υπάρχει πρώτη ρίζα μετα το
,
,
.
συνεχής
Αρα θα υπάρχουν ακολουθίεςμε
και
ώστεκαι
.
Aπό KΠ
Άρα
AΤΟΠΟσυνεχής
Σημείωση: Aν δεν υπάρχουν τέτοιες ακολουθιές τότε υπάρχει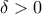
1η περίπτωση :με
2η περίπτωση :με
Kαι στις δύο περιπτώσεις προκύπτει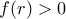
 με
με  και
και 
 και
και  .
.
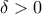
 με
με 
 με
με 
Καλύτερα να πούμε έστω ότι υπάρχουν ακολουθίεςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Φεβ 03, 2018 10:32 pmΑρα θα υπάρχουν ακολουθίεςmikemoke έγραψε: ↑Πέμ Φεβ 01, 2018 1:43 pmΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Σεπ 09, 2016 11:54 amΕστωπαραγωγίσιμη
ανοικτό διάστημα και
Εστωσυνεχής.
Ισχύει ότι
Αν
τότε η εξίσωσηδεν έχει ρίζα στο

και
συνεχής άρα δεν παρουσιάζει συσσώρευση ριζών στο
.Έστω ότι υπάρχει πρώτη ρίζα μετα το
,
,
.
συνεχής
Αρα θα υπάρχουν ακολουθίεςμε
και
ώστεκαι
.
Aπό κριτήριο παρεμβολής
Άρα
AΤΟΠΟσυνεχής
Σημείωση: Aν δεν υπάρχουν τέτοιες ακολουθιές τότε υπάρχει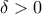
1η περίπτωση :με
2η περίπτωση :με
Kαι στις δύο περιπτώσεις προκύπτει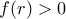
με
και
ώστεκαι
.
Aπό κριτήριο παρεμβολής
Σημείωση: Aν δεν υπάρχουν τέτοιες ακολουθιές τότε υπάρχει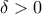
1η περίπτωση :με
2η περίπτωση :με
Μιχάλη αν έχεις την ευγενή καλοσύνη εξήγησε πως προκύπτουν
αυτά που έχω αντιγράψει.
 με
με  και
και 
 και
και  .
.
 τότε θα υπάρχει
τότε θα υπάρχει 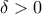 τέτοιο ώστε
τέτοιο ώστε με
με 
 με
με  (1).
(1). 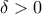 τότε θα μπορούμε να θεωρήσουμε τις παραπάνω ακολουθίες.
τότε θα μπορούμε να θεωρήσουμε τις παραπάνω ακολουθίες.
 είναι αύξουσα.
είναι αύξουσα. και
και  η ευθεία που διέρχεται από
η ευθεία που διέρχεται από
 αύξουσα
αύξουσα 
 υπάρχει
υπάρχει  τέτοιο ώστε
τέτοιο ώστε 
 άρα
άρα  .Επομένως πρέπει να υπάρχουν οι παραπάνω ακολουθίες.
.Επομένως πρέπει να υπάρχουν οι παραπάνω ακολουθίες.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης