με υγεία και μόνο χαρές!
(1) Έστω
![f:[0,1]\to\mathbb{R} f:[0,1]\to\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/2f88c23f13b9b1904c39f298cd688669.png) ολοκληρώσιμη. Δείξτε ότι
ολοκληρώσιμη. Δείξτε ότι 
(2) Συγκλίνουν οι σειρές:
(i)
 και
και(ii)
 όπου
όπου 
Συντονιστής: emouroukos
![f:[0,1]\to\mathbb{R} f:[0,1]\to\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/2f88c23f13b9b1904c39f298cd688669.png) ολοκληρώσιμη. Δείξτε ότι
ολοκληρώσιμη. Δείξτε ότι 
 και
και όπου
όπου 
Αντώνη αυτή είναι πολύ ωραία άσκηση. Όταν την είχα πρωτοσυναντήσει (πάνε κοντά 3 χρόνια τώρα) η πρώτη μου εντύπωση ήταν ότι "Δε μπορεί θα συγκλίνει" . Έλα ντε, που δε συγκλίνει. Θα χρησιμοποιήσουμε τη γνωστή ανισότηταAntonis Loutraris έγραψε: (2) Συγκλίνει η σειρά:
(i)
 . Από την ανισότητα Hermite - Hadamard έχουμε ότι:
. Από την ανισότητα Hermite - Hadamard έχουμε ότι: άρα "εκθετίζοντας" έχουμε:
άρα "εκθετίζοντας" έχουμε: Συνεπώς
Συνεπώς  και η σειρά αποκλίνει.
και η σειρά αποκλίνει.
ΈστωAntonis Loutraris έγραψε: (1) Έστωολοκληρώσιμη. Δείξτε ότι
 φράγμα της
φράγμα της  . Τότε
. Τότε 
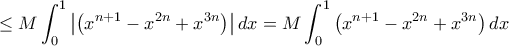
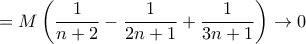
ΘέτουμεAntonis Loutraris έγραψε:
(ii)όπου
 και διακρίνουμε δύο περιπτώσεις.
και διακρίνουμε δύο περιπτώσεις. συγκλίνει.
συγκλίνει.
 αποκλίνει, που σημαίνει ότι
αποκλίνει, που σημαίνει ότι  ως γνήσια αύξουσα.
ως γνήσια αύξουσα.

 είναι αύξουσα.
είναι αύξουσα.
Και αλλιώς:Antonis Loutraris έγραψε: (i)


 .
.Μπορούμε να βελτιώσουμε την απόδειξη. Δεν χρειάζεται να διακρίνουμε δύο περιπτώσεις αλλά ένας σμπάρος αρκεί:Mihalis_Lambrou έγραψε:Antonis Loutraris έγραψε:
(ii)όπου
 ). Οπότε ακολουθούμε την διαδικασία που απομόνωσα παραπάνω αλλά στο τελευταίο βήμα γράφουμε
). Οπότε ακολουθούμε την διαδικασία που απομόνωσα παραπάνω αλλά στο τελευταίο βήμα γράφουμε 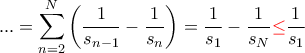 . Τελειώσαμε.
. Τελειώσαμε. , δείξτε ότι η σειρά
, δείξτε ότι η σειρά 

ΘέτουμεMihalis_Lambrou έγραψε:'Ενα συμπλήρωμα της τρίτης άσκησης που έθεσε ο Αντώνης παραπάνω:
Αν, δείξτε ότι η σειρά

συγκλίνει αν και μόνον αν συγκλίνει η
 και
και 

 ώστε για
ώστε για 

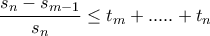
 (1)
(1)
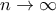
 ΑΤΟΠΟ.
ΑΤΟΠΟ.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 35 επισκέπτες