α) Ορίζουμε

για την οποία

και επειδή τα σημεία μηδενισμού της είναι μεμονωμένα και σε αυτά η

είναι συνεχής, άρα η

είναι γνησίως αύξουσα σε όλο το

οπότε είναι και 1-1 άρα ορίζεται η αντίστροφη. Επίσης

κι επειδή

άρα

.
Όμοια από την

βγάζουμε ότι

κι έτσι

.
Συνεπώς για κάθε

η αρχική σχέση δίνει

και αφού η

είναι αντιστρέψιμη με σύνολο τιμών το

, παίρνουμε

οπότε η

είναι καλώς ορισμένη.
Επίσης από την αρχική σχέση παίρνουμε

και αφού

άρα

Όμοια από την αρχική σχέση παίρνουμε

κι έτσι παίρνουμε

Έτσι, αφού η

είναι συνεχής έχει σύνολο τιμών το

.
β) Αφού η

είναι περιττή άρα και η αντίστροφη είναι περιττή. Επίσης η

είναι περιττή άρα η σύνθεσή τους

είναι επίσης περιττή άρα η

είναι περιττή.
γ) Είναι φανερές οι ισοδυναμίες

κι έτσι αρκεί να δείξουμε ότι η εξίσωση

έχει ακριβώς τρεις ρίζες.
Ορίζουμε

με

και

άρα η

είναι γνησίως αύξουσα και αφού

άρα

για

και

για

.
Έτσι, η

είναι γνησίως φθίνουσα στο
![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png)
και γνησίως αύξουσα στο
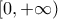
. Είναι

και αφού

και

άρα η

έχει ακριβώς δύο ρίζες

με

.
Τελικά, η

είναι γνησίως αύξουσα στο
![(-\infty, x_2] (-\infty, x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/52500931894db8088b360c09b2a375bb.png)
, γνησίως φθίνουσα στο
![[x_2,x_1] [x_2,x_1]](/forum/ext/geomar/texintegr/latexrender/pictures/7ac867c026c0708cf736b7f51188c2d8.png)
και γνησίως αύξουσα στο

άρα η

έχει το πολύ τρεις ρίζες μία σε κάθε ένα από αυτά τα διαστήματα. Η μία από αυτές είναι το

. Έτσι

και επειδή

και
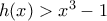
άρα

και

κι έτσι η

έχει ακριβώς από μία ρίζα σε κάθε ένα από τα διαστήματα

και

. Συνολικά λοιπόν ακριβώς τρεις ρίζες.
δ) Προφανώς οι θέσεις των ακροτάτων είναι (από προηγούμενο ερώτημα) το σημείο

(στο οποίο παρουσιάζει τοπικό μέγιστο) και το
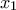
(στο οποίο παρουσιάζει τοπικό ελάχιστο). Το
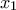
είναι ρίζα της

κι έτσι

.
Επειδή

άρα

άρα

κι έτσι

Επιπλέον είναι εύκολο να δείξουμε ότι για

ισχύει

κι έτσι

άρα

κι έτσι
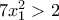
δηλαδή

.
Αλέξανδρος
 για την οποία ισχύει
για την οποία ισχύει  για κάθε
για κάθε 
 και ότι
και ότι 

 για την οποία
για την οποία  και επειδή τα σημεία μηδενισμού της είναι μεμονωμένα και σε αυτά η
και επειδή τα σημεία μηδενισμού της είναι μεμονωμένα και σε αυτά η  είναι συνεχής, άρα η
είναι συνεχής, άρα η  οπότε είναι και 1-1 άρα ορίζεται η αντίστροφη. Επίσης
οπότε είναι και 1-1 άρα ορίζεται η αντίστροφη. Επίσης  κι επειδή
κι επειδή  άρα
άρα  .
. βγάζουμε ότι
βγάζουμε ότι  κι έτσι
κι έτσι  .
. η αρχική σχέση δίνει
η αρχική σχέση δίνει  και αφού η
και αφού η  οπότε η
οπότε η  είναι καλώς ορισμένη.
είναι καλώς ορισμένη. και αφού
και αφού  άρα
άρα 
 κι έτσι παίρνουμε
κι έτσι παίρνουμε 
 είναι περιττή άρα η σύνθεσή τους
είναι περιττή άρα η σύνθεσή τους  είναι επίσης περιττή άρα η
είναι επίσης περιττή άρα η  κι έτσι αρκεί να δείξουμε ότι η εξίσωση
κι έτσι αρκεί να δείξουμε ότι η εξίσωση  με
με  και
και  άρα η
άρα η  είναι γνησίως αύξουσα και αφού
είναι γνησίως αύξουσα και αφού  άρα
άρα  για
για  και
και  για
για  .
. είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 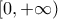 . Είναι
. Είναι  και αφού
και αφού  και
και  άρα η
άρα η  με
με  .
. είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(-\infty, x_2] (-\infty, x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/52500931894db8088b360c09b2a375bb.png) , γνησίως φθίνουσα στο
, γνησίως φθίνουσα στο ![[x_2,x_1] [x_2,x_1]](/forum/ext/geomar/texintegr/latexrender/pictures/7ac867c026c0708cf736b7f51188c2d8.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  άρα η
άρα η  έχει το πολύ τρεις ρίζες μία σε κάθε ένα από αυτά τα διαστήματα. Η μία από αυτές είναι το
έχει το πολύ τρεις ρίζες μία σε κάθε ένα από αυτά τα διαστήματα. Η μία από αυτές είναι το  . Έτσι
. Έτσι  και επειδή
και επειδή  και
και 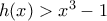 άρα
άρα  και
και  κι έτσι η
κι έτσι η  και
και  . Συνολικά λοιπόν ακριβώς τρεις ρίζες.
. Συνολικά λοιπόν ακριβώς τρεις ρίζες. (στο οποίο παρουσιάζει τοπικό μέγιστο) και το
(στο οποίο παρουσιάζει τοπικό μέγιστο) και το 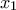 (στο οποίο παρουσιάζει τοπικό ελάχιστο). Το
(στο οποίο παρουσιάζει τοπικό ελάχιστο). Το  κι έτσι
κι έτσι  .
. άρα
άρα  άρα
άρα  κι έτσι
κι έτσι 
 κι έτσι
κι έτσι  άρα
άρα  κι έτσι
κι έτσι 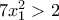 δηλαδή
δηλαδή  .
.