 συνεχείς στο
συνεχείς στο ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png) να δείξετε
να δείξετεΑ)υπάρχει

B)υπάρχει

Γ)υπάρχει

χίλια συγνωμη στα Δ,E
![\displaystyle{f(x)\ge 0,\xi \in [a,b]}</span>} \displaystyle{f(x)\ge 0,\xi \in [a,b]}</span>}](/forum/ext/geomar/texintegr/latexrender/pictures/28a5d82c52db45ebd94238cf1ed6357f.png)
Δ))υπάρχει
![\displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(\xi) \int_{a}^{b}{f(t)dt} \displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(\xi) \int_{a}^{b}{f(t)dt}](/forum/ext/geomar/texintegr/latexrender/pictures/46367c31d3f65f709ea926465b5002a5.png)
E)υπάρχει
![\displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(a) \int_{a}^{\xi}{f(t))dt}+g(b) \int_{\xi}^{b}{f(t)dt} \displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(a) \int_{a}^{\xi}{f(t))dt}+g(b) \int_{\xi}^{b}{f(t)dt}](/forum/ext/geomar/texintegr/latexrender/pictures/5980f76e9f5592e29248b17ac75a4e98.png)
Συντονιστής: emouroukos
 συνεχείς στο
συνεχείς στο ![\displaystyle{[a,b]} \displaystyle{[a,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/14f53999651f504e8f7c5c1b74530f3e.png) να δείξετε
να δείξετε


![\displaystyle{f(x)\ge 0,\xi \in [a,b]}</span>} \displaystyle{f(x)\ge 0,\xi \in [a,b]}</span>}](/forum/ext/geomar/texintegr/latexrender/pictures/28a5d82c52db45ebd94238cf1ed6357f.png)
![\displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(\xi) \int_{a}^{b}{f(t)dt} \displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(\xi) \int_{a}^{b}{f(t)dt}](/forum/ext/geomar/texintegr/latexrender/pictures/46367c31d3f65f709ea926465b5002a5.png)
![\displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(a) \int_{a}^{\xi}{f(t))dt}+g(b) \int_{\xi}^{b}{f(t)dt} \displaystyle{\xi \in [a,b] . \int_{a}^{b}{f(t)g(t)dt}=g(a) \int_{a}^{\xi}{f(t))dt}+g(b) \int_{\xi}^{b}{f(t)dt}](/forum/ext/geomar/texintegr/latexrender/pictures/5980f76e9f5592e29248b17ac75a4e98.png)

 δεν υπάρχει
δεν υπάρχει 


 .
. είναι μονότονη και η
είναι μονότονη και η  Riemann ολοκληρώσιμη.
Riemann ολοκληρώσιμη. παραγωγίσιμη αφού
παραγωγίσιμη αφού  συνεχής. Από το ΘΜΤ για παραγώγους
συνεχής. Από το ΘΜΤ για παραγώγους  ή
ή 
 είναι
είναι 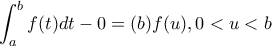 .θετω
.θετω  οπότε
οπότε  και έτσι
και έτσι 
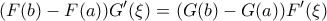 όπoυ
όπoυ  αρχικές των
αρχικές των  τότε
τότε 

 απο το προηγούμενο για
απο το προηγούμενο για  είναι
είναι  ή
ή 
 συνεχης αρα
συνεχης αρα  μονότονη τότε
μονότονη τότε![\displaystyle{\int_{a}^{x}f(t)g(t)dt=\int_{a}^{x}f(t)G'(t)dt=[f(x)G(x)-0]-\int_{a}^{x}f'(t)G(t)dt.} \displaystyle{\int_{a}^{x}f(t)g(t)dt=\int_{a}^{x}f(t)G'(t)dt=[f(x)G(x)-0]-\int_{a}^{x}f'(t)G(t)dt.}](/forum/ext/geomar/texintegr/latexrender/pictures/2964484e94419b81d9247c06b16da6a5.png) Aπό το Δ) ομως είναι
Aπό το Δ) ομως είναι αρα
αρα
![\displaystyle{\int_{a}^{b}f(t)G'(t)dt=[f(b)G(b)-0]-\int_{a}^{b}f'(t)G(t)dt.}=} \displaystyle{\int_{a}^{b}f(t)G'(t)dt=[f(b)G(b)-0]-\int_{a}^{b}f'(t)G(t)dt.}=}](/forum/ext/geomar/texintegr/latexrender/pictures/89bb043f652c1118dc312051c1460686.png)
![\displaystyle{\int_{a}^{b}f(t)G'(t)dt=[f(b)G(b)-0]-\int_{a}^{b}f'(t)G(t)dt.}=} \displaystyle{\int_{a}^{b}f(t)G'(t)dt=[f(b)G(b)-0]-\int_{a}^{b}f'(t)G(t)dt.}=}](/forum/ext/geomar/texintegr/latexrender/pictures/89bb043f652c1118dc312051c1460686.png)



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες