 ἀκολουθία θετικῶν ἀριθμῶν ὥστε
ἀκολουθία θετικῶν ἀριθμῶν ὥστε 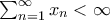 . Θέτομε
. Θέτομε
Δείξατε ὅτι ἡ σειρὰ

συγκλίνει.
Συντονιστής: emouroukos
 ἀκολουθία θετικῶν ἀριθμῶν ὥστε
ἀκολουθία θετικῶν ἀριθμῶν ὥστε 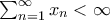 . Θέτομε
. Θέτομε

![limsup\sqrt[n]{\frac{n^{2}}{x_{n}S{_{n}^{2}}}}< 1 limsup\sqrt[n]{\frac{n^{2}}{x_{n}S{_{n}^{2}}}}< 1](/forum/ext/geomar/texintegr/latexrender/pictures/522d5decfefece791a16294101245c69.png)
![S_{n}= \frac{1}{x_{1}}+\frac{1}{x_{2}}+....+\frac{1}{x_{n}}>\frac{1}{x_{n}}\Rightarrow S_{n}^{2}>\frac{1}{x_{n}^{2}}\Rightarrow x_{n}S_{n}^{2}>\frac{1}{x_{n}}\Rightarrow \frac{1}{x_{n}S_{n}^{2}}< x_{n}\Rightarrow \frac{n^{2}}{x_{n}S_{n}^{2}}< n^{2}x_{n}\Rightarrow \sqrt[n]{\frac{n^{2}}{x_{n}S_{n}^{2}}}< \sqrt[n]{n^{2}x_{n}} S_{n}= \frac{1}{x_{1}}+\frac{1}{x_{2}}+....+\frac{1}{x_{n}}>\frac{1}{x_{n}}\Rightarrow S_{n}^{2}>\frac{1}{x_{n}^{2}}\Rightarrow x_{n}S_{n}^{2}>\frac{1}{x_{n}}\Rightarrow \frac{1}{x_{n}S_{n}^{2}}< x_{n}\Rightarrow \frac{n^{2}}{x_{n}S_{n}^{2}}< n^{2}x_{n}\Rightarrow \sqrt[n]{\frac{n^{2}}{x_{n}S_{n}^{2}}}< \sqrt[n]{n^{2}x_{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/30eb91179638f906aff675389c00b776.png)
![limsup\sqrt[n]{\frac{n^{2}}{x_{n}S^{2}_{n}}}\leq limsup\sqrt[n]{n^{2}x_{n}} limsup\sqrt[n]{\frac{n^{2}}{x_{n}S^{2}_{n}}}\leq limsup\sqrt[n]{n^{2}x_{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/205b9cb62ab5ad275749f5f7c676f9f2.png)
![limsup\sqrt[n]{n^{2}x_{n}}\leq limsup(\left ( \frac{n+1}{n} \right )^{2}\cdot \frac{x_{n+1}}{x_{n}}) limsup\sqrt[n]{n^{2}x_{n}}\leq limsup(\left ( \frac{n+1}{n} \right )^{2}\cdot \frac{x_{n+1}}{x_{n}})](/forum/ext/geomar/texintegr/latexrender/pictures/c22c87e250b8976466312794959806f0.png)

 είναι μικρότερο του 1 διότι διαφορετικά η ακολουθία
είναι μικρότερο του 1 διότι διαφορετικά η ακολουθία  θα είχε μια αύξουσα υπ ακολουθία και άρα δεν θα ήταν μηδενική όπως προκύπτει από τη σύγκλιση της σειράς της.
θα είχε μια αύξουσα υπ ακολουθία και άρα δεν θα ήταν μηδενική όπως προκύπτει από τη σύγκλιση της σειράς της.![\displaystyle{
\limsup_{n\to\infty}\sqrt[n]{x_n}<1.
} \displaystyle{
\limsup_{n\to\infty}\sqrt[n]{x_n}<1.
}](/forum/ext/geomar/texintegr/latexrender/pictures/6afb6670a264167bc866cfda5c3e1672.png)
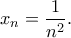
Ούτε αυτό ισχύει. Για παράδειγμα ηΠαπαστεργίου Κώστας έγραψε: Τώρα τοείναι μικρότερο του 1 διότι διαφορετικά η ακολουθία
θα είχε μια αύξουσα υπ ακολουθία
 έχει
έχει  αλλά δεν έχει αύξουσα υπακολουθία.
αλλά δεν έχει αύξουσα υπακολουθία. τότε η
τότε η  θα είχε μια υπ ακολουθία ας πούμε
θα είχε μια υπ ακολουθία ας πούμε  η οποία θα είχε όριο το
η οποία θα είχε όριο το  επομένως θα ήταν τελικά
επομένως θα ήταν τελικά 
 δηλαδή η υπ ακολουθία
δηλαδή η υπ ακολουθία  της
της  θα ήταν αύξουσα με θετικούς όρους, άρα μη μηδενική.
θα ήταν αύξουσα με θετικούς όρους, άρα μη μηδενική.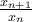
 ή η
ή η  ; Η μία συγκλίνει στο άπειρο και η άλλη στο μηδέν. Ελπίζω να μην έχουμε άλλες λαχτάρες.
; Η μία συγκλίνει στο άπειρο και η άλλη στο μηδέν. Ελπίζω να μην έχουμε άλλες λαχτάρες. Για παράδειγμα αν ο πρώτος όροςΠαπαστεργίου Κώστας έγραψε: θα ήταν τελικά
δηλαδή η υπ ακολουθία
της
θα ήταν αύξουσα με θετικούς όρους
 ήταν ο
ήταν ο 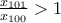 και ο επόμενος όρος μεγαλύτερος του
και ο επόμενος όρος μεγαλύτερος του  είναι ο
είναι ο  , τότε
, τότε  αλλά δεν ισχύει κατ' ανάγκη
αλλά δεν ισχύει κατ' ανάγκη  όπως ισχυρίζεσαι. Συγκεκριμένα, το λάθος σου είναι ότι ονόμασες
όπως ισχυρίζεσαι. Συγκεκριμένα, το λάθος σου είναι ότι ονόμασες  και
και 
 έχει ήδη χρησιμοποιηθεί. Το δεύτερο κλάσμα των
έχει ήδη χρησιμοποιηθεί. Το δεύτερο κλάσμα των  πρέπει να γραφεί ως
πρέπει να γραφεί ως 
 δεν είναι κατ' ανάγκη μεγαλύτερος από τον προηγούμενό του (εδώ η
δεν είναι κατ' ανάγκη μεγαλύτερος από τον προηγούμενό του (εδώ η  έχει πρόβλημα). Το παράδειγμα που έδωσα το καθιστά σαφές.
έχει πρόβλημα). Το παράδειγμα που έδωσα το καθιστά σαφές. Είναι ηΠαπαστεργίου Κώστας έγραψε:Ποια είναι η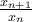
Είναι ηή η
;
 για
για  περιττό και η
περιττό και η  για
για  άρτιο.
άρτιο.  . Πάντως το
. Πάντως το  είναι
είναι  και δεν υπάρχει αύξουσα υπακολουθία (προφανές).
και δεν υπάρχει αύξουσα υπακολουθία (προφανές).Επαναφορά.Γ.-Σ. Σμυρλής έγραψε:Ἔστωἀκολουθία θετικῶν ἀριθμῶν ὥστε
. Θέτομε
Δείξατε ὅτι ἡ σειρὰ

συγκλίνει.

 έχω
έχω
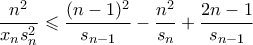
 συγκλίνει τηλεσκοπικά στο
συγκλίνει τηλεσκοπικά στο  . Αρκεί λοιπόν να δείξω ότι συγκλίνει και η
. Αρκεί λοιπόν να δείξω ότι συγκλίνει και η 

 )
)


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες