 ,
,  , είναι ευρέως γνωστή .
, είναι ευρέως γνωστή .Ήρθε η ώρα να δείξουμε και την :
 ,
, 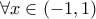 .
.Συντονιστής: emouroukos
 ,
,  , είναι ευρέως γνωστή .
, είναι ευρέως γνωστή . ,
, 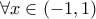 .
. για την οποία ισχύει
για την οποία ισχύει  .
. . Επειδή
. Επειδή  και ισχύει
και ισχύει  για
για 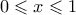 , παίρνουμε
, παίρνουμε  για
για 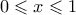 . Έτσι, από ΘΜΤ, έχουμε
. Έτσι, από ΘΜΤ, έχουμε  .
. για
για  . Έτσι, από ΘΜΤ, έχουμε
. Έτσι, από ΘΜΤ, έχουμε  και πάλι από ΘΜΤ
και πάλι από ΘΜΤ  .
. για
για ![x\in(-1,0] x\in(-1,0]](/forum/ext/geomar/texintegr/latexrender/pictures/18182069f90f0f2d90c75bb3c60edce3.png) παίρνουμε:
παίρνουμε: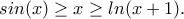 Άρα αρκεί να αποδείξουμε ότι
Άρα αρκεί να αποδείξουμε ότι  για κάθε
για κάθε 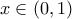 .
.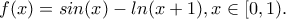
 Θα δείξουμε ότι για κάθε
Θα δείξουμε ότι για κάθε  είναι
είναι  με την ισότητα να ισχύει μόνο για
με την ισότητα να ισχύει μόνο για  .
.  και η
και η  είναι κοίλη στο
είναι κοίλη στο  ενώ η
ενώ η 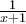 κυρτή στο
κυρτή στο  . Άρα αρκεί να είναι
. Άρα αρκεί να είναι  το οποίο προφανώς ισχύει αφού
το οποίο προφανώς ισχύει αφού 
 και επομένως
και επομένως 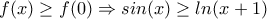 με την ισότητα να ισχύει μόνο για
με την ισότητα να ισχύει μόνο για  .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 9 επισκέπτες