 το σύνολο των συνεχών συναρτήσεων
το σύνολο των συνεχών συναρτήσεων ![\displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1] \displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ea72d5caf58979184c0297eee0f99361.png)
που είναι παραγωγίσιμες στο
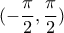
Να υπολογισθεί το
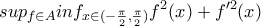
Το θέμα είναι σε άλλη μορφή δημοσιευμένο στο f.b
Μετά την λύση θα αναφέρω και αυτόν που το ανάρτησε.
Συντονιστής: emouroukos
 το σύνολο των συνεχών συναρτήσεων
το σύνολο των συνεχών συναρτήσεων ![\displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1] \displaystyle f:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ea72d5caf58979184c0297eee0f99361.png)
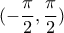
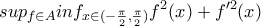
 υπάρχει
υπάρχει 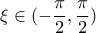 , ώστε
, ώστε 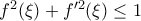 .
. όχι μονότονη, η παράγωγος κάπου θα μηδενίζεται και η θέση αυτή μας κάνει ως
όχι μονότονη, η παράγωγος κάπου θα μηδενίζεται και η θέση αυτή μας κάνει ως  .
. μονότονη, έστω αύξουσα, τότε, αν δεν κάνω λάθος, η παράγωγός της είναι ολοκληρώσιμη.
μονότονη, έστω αύξουσα, τότε, αν δεν κάνω λάθος, η παράγωγός της είναι ολοκληρώσιμη.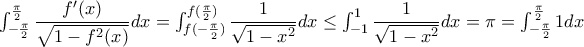 .
. ,ώστε
,ώστε 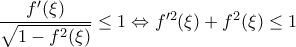 .
.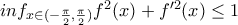 .
. πιάνεται με τη συνάρτηση
πιάνεται με τη συνάρτηση  , έπεται ότι η ζητούμενη τιμή είναι το
, έπεται ότι η ζητούμενη τιμή είναι το  .
.Η λύση είναι εντάξει.ksofsa έγραψε: ↑Σάβ Σεπ 09, 2023 10:27 pmΚαλησπέρα.
Μια προσπάθεια:
ΛΗΜΜΑ: Για κάθευπάρχει
, ώστε
.
Ανόχι μονότονη, η παράγωγος κάπου θα μηδενίζεται και η θέση αυτή μας κάνει ως
.
Ανμονότονη, έστω αύξουσα, τότε, αν δεν κάνω λάθος, η παράγωγός της είναι ολοκληρώσιμη.
Οπότε:
.
Συνεπώς, υπάρχει,ώστε
.
Ερχόμαστε στο πρόβλημα.
Από το λήμμα είναι άμεσο ότι.
Επειδή τοπιάνεται με τη συνάρτηση
, έπεται ότι η ζητούμενη τιμή είναι το
.
Ισχύει για ολοκλήρωμα Lebesgue.
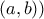 και η
και η ![f:[a,b]\rightarrow \mathbb{R} f:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/cbf6bcd3aa5cc7cdf73d8d1c12387715.png) είναι συνεχής τότε
είναι συνεχής τότε 
 και
και 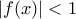 στο
στο 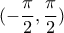
![g:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-\frac{\pi }{2},\frac{\pi }{2}] g:[-\frac{\pi }{2},\frac{\pi }{2}]\rightarrow [-\frac{\pi }{2},\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/25273435da0cd3ab65704ec9f9e1a853.png)
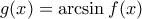 είναι συνεχής και παραγωγίσημη στο
είναι συνεχής και παραγωγίσημη στο 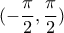 .
.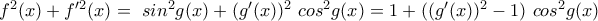
 υπάρχει
υπάρχει 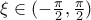
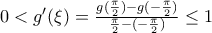
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 4 επισκέπτες