Αν η συνάρτηση
 είναι παραγωγίσιμη στο διάστημα
είναι παραγωγίσιμη στο διάστημα 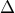 και
και 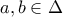 έτσι ώστε
έτσι ώστε 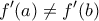 τότε για κάθε
τότε για κάθε  μεταξύ των
μεταξύ των 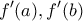 θα υπάρχει
θα υπάρχει 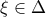 τέτοιο ώστε:
τέτοιο ώστε: 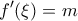 .
.Απόδειξη.
- 1. Αν μια συνάρτηση
 είναι παραγωγίσιμη στο διάστημα
είναι παραγωγίσιμη στο διάστημα 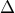 και
και 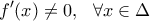 τότε η
τότε η  είναι
είναι  .
.
Η απόδειξη είναι εύκολη με άτοπο και χρήση του θεωρήματος Rolle.
- 2. Αν μια συνάρτηση
 είναι συνεχής και
είναι συνεχής και  στο διάστημα
στο διάστημα 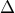 τότε είναι γνησίως μονότονη.
τότε είναι γνησίως μονότονη.
Η απόδειξη με άτοπο και χρήση του θεωρήματος ενδιάμεσων τιμών συνεχούς συνάρτησης.
- 3. Αν μια συνάρτηση
 είναι παραγωγίσιμη στο διάστημα
είναι παραγωγίσιμη στο διάστημα 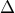 και υπάρχουν
και υπάρχουν 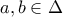 τέτοια ώστε
τέτοια ώστε 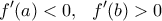 , τότε θα υπάρχει
, τότε θα υπάρχει 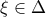 τέτοιο ώστε:
τέτοιο ώστε: 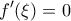 .
.
Απόδειξη
Έστω ότι το ζητούμενο δεν ισχύει. Θα είναι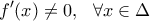
Από 1., 2. η είναι γνησίως μονότονη. Έστω ότι είναι γνησίως αύξουσα - ομοίως αν είναι γνησίως φθίνουσα.
είναι γνησίως μονότονη. Έστω ότι είναι γνησίως αύξουσα - ομοίως αν είναι γνησίως φθίνουσα.
Ισχύει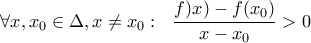 οπότε
οπότε 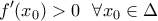 . Άτοπο.
. Άτοπο.
 .
.


 να βρίσκεται μεταξύ
να βρίσκεται μεταξύ και
και  , που είναι και η ουσία του θεωρήματος.
, που είναι και η ουσία του θεωρήματος.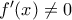 για κάθε
για κάθε  σε ένα διάστημα, τότε η
σε ένα διάστημα, τότε η  διατηρεί το πρόσημό της. Έστω λοιπόν, χωρίς βλάβη,
διατηρεί το πρόσημό της. Έστω λοιπόν, χωρίς βλάβη, 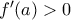 .
.  έπεται (ως γνωστόν) ότι η
έπεται (ως γνωστόν) ότι η  είναι
είναι  . Άρα, ως συνεχής, από το θεώρημα ενδιάμεσων τιμών, είναι γνησίως μονότονη σε όλο το διάστημα. Μάλιστα από την
. Άρα, ως συνεχής, από το θεώρημα ενδιάμεσων τιμών, είναι γνησίως μονότονη σε όλο το διάστημα. Μάλιστα από την 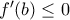 , ισοδύναμα
, ισοδύναμα 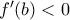 (διότι
(διότι 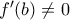 ), διότι τότε γύρω από το
), διότι τότε γύρω από το 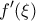 και όχι του
και όχι του  .
. αλλάζοντας την διατύπωση της πρότασης, με το διάστημα
αλλάζοντας την διατύπωση της πρότασης, με το διάστημα